Пояснительная записка
Урок изучения нового материала по теме "Непозиционные системы счисления" разработан для учащихся 5 класса изучающих материал по учебнику "Математика, 5" Гельфман Э.Г. и др.
Урок по теме «Непозиционные системы счисления» является первым уроком по данной теме, это урок знакомства с новым учебным материалом. Для того чтобы урок прошел интересно, успешно, чтобы учащиеся работали активно, необходима предварительно большая подготовительная работа учителя и отдельных учащихся. В ходе подготовки к уроку было изучено много дополнительной справочной и исторической литературы, в связи с тем, что в данном учебнике материал представлен в малом объеме, а во многих УМК этот материал и вовсе не рассматривают.
Урок состоит из следующих основных этапов:
Актуализация опорных знаний
Введение в тему, постановка учебных задач
Изучение нового материала в ходе лекции с элементами беседы и сообщения учащегося
Первичное осмысление и закрепление учебного материала
Подведение итогов урока, рефлексия, запись и обсуждение домашнего задания.
Использование на уроке информационно-коммуникационных технологий (презентация к уроку) способствует увеличению количества заданий рассматриваемых на уроке, позволяет сделать урок ярким и интересным для учащихся, повышает интерес к предмету.
Цель:
Познакомить с понятием непозиционной системы счисления и различными её видами;
Повышение интереса к предмету за счет использования богатого исторического и наглядного материала;
Расширение кругозора учащихся;
Развитие речи, умения лаконично излагать свои мысли, анализировать и делать выводы;
Развитие коммуникативных навыков; умения работать в группе;
Сценарий учебного занятия
Цели:
Образовательные:
Повторить понятие непозиционной системы счисления;
Знакомство с основными непозиционными системами счисления существовавшими ранее;
Отработать знания и умения перевода чисел из различных систем счисления в арабскую запись и наоборот.
Развивающие:
Работать над развитием понятийного аппарата;
Развивать навыки самоконтроля;
Развивать познавательную активность;
Развивать культуру учебной деятельности;
Развивать осмысленное отношение к своей деятельности;
Развивать самостоятельность мышления, видеть общую закономерность и делать обобщенные выводы.
Воспитательные:
Воспитывать ответственное отношение к учению;
Воспитывать волю и настойчивость для достижения конечных результатов;
Воспитывать аккуратность;
Воспитывать культуру общения.
Формы работы: индивидуальная работа, самостоятельная работа, фронтальный, индивидуальный опрос.
Структура урока:
Организационный момент
Актуализация опорных знаний
Введение в тему, постановка учебных задач
Изучение нового материала
Первичное осмысление и закрепление учебного материала
Рефлексия
Запись и обсуждение домашнего задания
Подведение итога урока, анкетирование
Ход урока:
Организационный момент (приветствие, проверка готовности к уроку, объявление темы урока (слайд 2)).
Объяснение нового материала, исторический экскурс.
Вступительное слово учителя: Мы уже говорили о том, что цифры, которыми в наше время пользуются люди, были придуманы не сразу - они создавались постепенно и медленно входили в употребление. Цифры изобретались и видоизменялись на протяжении долгого времени, многих столетий с развитием письменности. Различные народы на протяжении долгого времени имели каждый свою нумерацию (слайд 3)
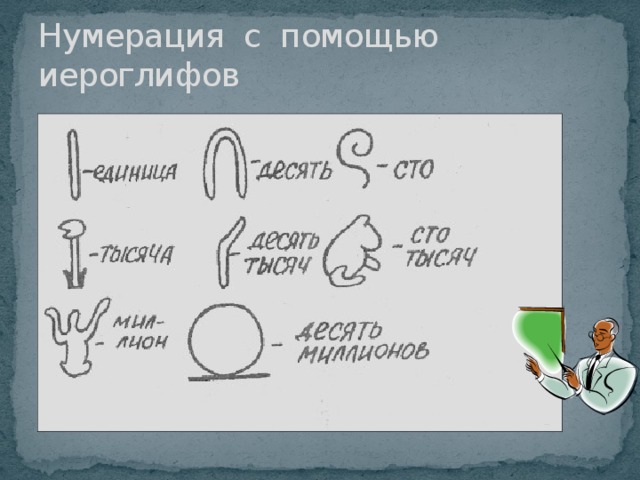
Так, египтяне, китайцы, жители Центральной Америки для записи чисел применяли картинки - иероглифы, которые изображали птиц, людей, зверей, части человеческого тела (слайд 4)
Выступление учащегося: В Китае, например, числа записываются с помощью вот таких особых знаков - иероглифов (слайд 5). Имеются знаки для записи чисел от 1 до 10, а также для числа 100 и 1000. На этом же плакате вы можете увидеть, как записывают более сложные числа с помощью этих иероглифов.
Вопрос учащимся: Давайте посмотрим на эти картинки, на что похожи знаки, изображающие эти числа? (варианты ответов учащихся)
Полагают, что иероглиф для числа сто изображает измерительную веревку, для тысячи - цветок лотоса, для десяти миллионов - всю Вселенную. Все остальные числа составлялись с помощью основных, с помощью сложения.
В древнейшее время в Греции была распространена так называемая аттическая нумерация. В этой нумерации числа 1,2,3,4 изображались с помощью соответствующего числа вертикальных полосок. Для чисел 5,10,50,100,500,1000,5000использовались свои определенные знаки (слайд 6).
Также с помощью иероглифов записывали числа и древние египтяне, они придумали свою систему 5000лет тому назад. Это одна из древнейших систем записи чисел. В ней есть иероглифы для чисел кратных 10, от единицы до миллиона (слайд 7.
Выступление учащегося:
Вавилоняне использовали для записи чисел клинопись. Они пользовались двумя знаками: прямым клином v-для записи числа один, и лежащим клином < для записи числа десять. Так, например, число 32 писалось следующим образом <<< VV.
Вавилонская система записи чисел переходит в Индию, где её совершенствуют. Индийская нумерация распространилась по всему миру. В страны Европы она была занесена арабами примерно 1000 лет назад, поэтому сейчас и сохранилось название арабские цифры.
У нас в России эти цифры стали применять лишь 250 лет назад. До этого же времени ниши предки пользовались славянской нумерацией или алфавитной. Славянская нумерация основана на следующем правиле: несколько букв под титлом (это черт очка вверху буквы), написанных рядом, обозначают число, равное сумме чисел, обозначаемых буквами. Первые девять букв обозначали единицы, следующие девять - десятки и остальные девять - сотни (слайд 8).
Большие числа записывались этими же буквами, но применялись специальные обозначения: слово «тысяча» заменял значок SHAPE * MERGEFORMAT , который ставился слева внизу около буквы.
Такой системой пользовались многие народы - арабы, армяне, грузины, славяне и другие народы.
Вопрос учащимся:
Как вы думаете, удобна ли алфавитная нумерация и почему? (варианты ответов учащихся). Можно заметить, что алфавитная нумерация удобна для обозначения небольших чисел (до тысячи). Где мы с вами в настоящее время можем встретить алфавитную нумерацию? (варианты ответов учащихся). Действительно, остатки этой нумерации в нашем обиходе сохранились и по сей день, для нумерации пунктов плана, при составлении конспекта.
Сейчас мы настолько привыкли к обозначению чисел с помощью десяти знаков (0,1,2,3,4,5,6,7,8,9), что не замечаем их удобства и простоты.
Но, несмотря на то, что индийская нумерация является международной, в некоторых странах применяется помимо индийской нумерации, ещё и своя, народная.
Остановимся на известной вам римской нумерации. Римской системой счисления пользовались в Европе в средние века, но и в настоящее время без неё нельзя обойтись во многих областях. Что вам известно про эту нумерацию? (ответы учащихся)
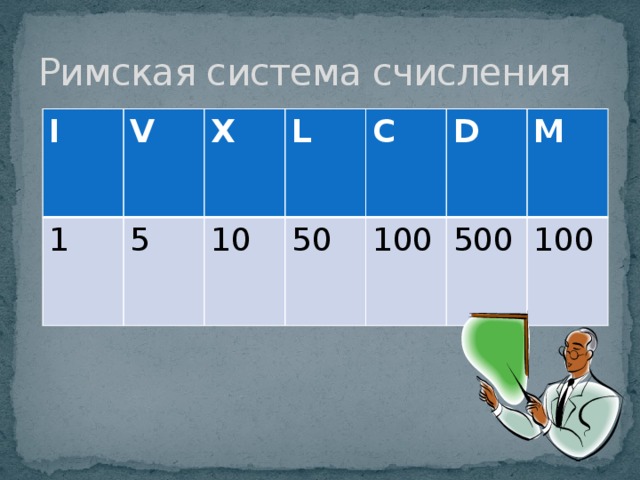
Надо отметить, что у римлян были специальные обозначения для чисел 1, 5, 10, 50, 100, 500, 1000. Римские цифры имели следующий вид (слайд 9).
Эти семь чисел назывались узловыми и с их помощью можно записать любое многозначное число. Первоначально римские цифры немного отличались от тех цифр, какими мы привыкли пользоваться сейчас. Они претерпели небольшие изменения в написании.
О происхождении римских цифр нет достоверных сведений, по этому поводу среди ученых до сих пор идут споры. Существует несколько взглядов на эту проблему.
Посмотрите внимательно на цифры 1, 5 и 10. На что они похожи? (1-палочка, 10-крест, мы видели их на обозначении группы крови, в учебнике истории). А есть ли что- то у человека, с чем можно связать эти обозначения? (один- один палец, 5-ладошка, рука, десять-две руки).
Действительно ребята, существует мнение, что цифры I,V,X есть суть палец, открытая рука и две такие руки.
Как записывать числа с использованием римской нумерации? (читают правила в учебнике с комментариями).
Если цифра с большим значением стоит слева от цифры с меньшим значением, то их значение складывается.
Например: 6- VI,11-XI, 60-LX
Если цифра с меньшим значением стоит слева от цифры с большим значением, то из большего вычитается меньшее.
Например: 4-IV, 9-IX, 40-XL,90-XC.
Если рядом стоят две одинаковые цифры, то их значение складывается.
Например: СС-200, XX-20.
Одна и та же цифра не может быть написана подряд более трех раз.
Все рассмотренные выше системы счисления являются непозиционными. Непозиционные системы - это такие, в которых значение знака не зависит от его положения в записи числа.
Практическое применение знаний.
Сейчас мы с вами научимся записывать числа с помощью славянской, египетской китайской, римской нумерации, и наоборот переходить из этих систем к записи чисел арабскими цифрами.
Задание №1 слайд 10(перейти от чисел в арабской нумерации к славянской)
Задание №2 слайд11(перейти от чисел в славянской нумерации к арабской)
Задание №3 слайд12(перейти от чисел в арабской нумерации к египетской и китайской)
Задание №4 слайд 13(перейти от чисел в китайской нумерации к арабской)
Задание №5 слайд 14(перейти от чисел в римской нумерации к арабской)
Задание №6 слайд 15(перейти от чисел в арабской нумерации к римской)
Подведение итогов урока. Этап рефлексии (цветовая рефлексия, слайд 16)
Запись и обсуждение домашнего задания (слайд 17)
Литература
Акимова С. Занимательная математика. Нескучный учебник. Санкт- Петербург. Тригон, 1997
Дорофеева А.В. Страницы истории на уроках математики. Львов, журнал «Кввантор» №6, 1991
Математика. Учебное пособие для 5 класса общеобразовательных учреждений. Гельфман Э.Г., Демидова Л.Н., Лобаненко Н.Б. и др. – М.: Просвещение, 2005.

 Получите свидетельство
Получите свидетельство Вход
Вход


























 Непозиционные системы счисления (0.96 MB)
Непозиционные системы счисления (0.96 MB)
 1
1 1342
1342 43
43 Нравится
0
Нравится
0




