Конспект урока по информатике "Быстрый перевод чисел"

Цель:

- Ознакомить учащихся с правилами быстрого перевода чисел из одной системы счисления в другую; закрепить перевод чисел в десятичную систему счисления и обратно;

- Развить логическое мышление, внимание, память, кругозор учащихся, интерес к предмету;

- Воспитать самостоятельность, аккуратность, ответственность, трудолюбие.

Ход урока.

1. Организационный момент.

Создание рабочей обстановки в классе.

- Здравствуйте, садитесь.

- Вот уже несколько уроков мы с вами посвятили довольно интересной теме, которая называется «Системы счисления». Сегодня на уроке мы должны еще раз вспомнить все, что касается данной темы, а также рассмотреть новый материал по данной теме.

- Итак, все готовы к работе?

Да.

- Тогда начнем… Для начала давайте поставим перед собой задачи, которые мы должны разрешить в течение нашего урока:

Задача 1. Вспомнить определения понятий, касающихся данной темы, историю систем счисления;

Задача 2. Изучить новый материал;

Задача 3. Закрепить изученный материал;

Задача 4. Выполнить работу за компьютером;

Задача 5. Выполнить гимнастику для глаз и физминутку;

Задача 6. Выполнить самостоятельную работу;

Задача 7. Подвести итоги урока.

2. Повторение изученного материала.

- Что называется системой счисления?

Система счисления – это определенный способ записи чисел и соответствующие ему правила действия над ними.

- А какой системой счисления мы с вами пользуемся в повседневной жизни?

Десятичной.

- Сколько цифр мы используем и что делаем с числами?

Используем 10 цифр, числа складываем и вычитаем поразрядно, умножаем столбиком и делим углом.

- Но вы знаете, что десятичная система счисления не сразу заняла свое господствующее положение, которое занимает сейчас. Раньше многие народы пользовались другими системами счисления. Так довольно широкое распространение имела двенадцатеричная система счисления.

Ее происхождение связано со счетом на пальцах руки (кроме большого) имеют 12 фаланг. По ним перебирали большим пальцем и вели счет от 1 до 12. В устной речи остатки 12-ой системы счисления сохранились до сих пор: вместо 12 мы часто говорим дюжина, многие предметы (ножи, вилки, тарелки и т. д. ) считают дюжинами, а не десятками. У англичан 1 фунт = 12 дюймов, 1 шиллинг = 12 пенсов.

В древнем Вавилоне широко была распространена шестидесятеричная система счисления, ее происхождение неизвестно, но есть гипотеза, что эта система счисления возникла как компромисс при объединении племен, пользовавшихся шестеричной и десятичной систем счисления. Эта система счисления была громоздкой и неудобной. Кстати, мы до сих пор в счете используем число 60. Что мы считаем по 60?

1 час=60 мин, 1 мин=60 сек, 1⁰=60' , 1' = 60''.

- Верно, итак, кроме рассмотренных систем счисления существовало и множество других систем счисления. Назовите еще несколько систем счисления, которые вы знаете.

А) Единичная система счисления – в записи чисел применялся только один вид знаков – палочка;

Б) Древнеегипетская десятинная непозиционная система счисления – возникла во 2-ой половине третьего тысячелетия до н. э, использовались специальные знаки:

В) Римская система счисления;

Г) Арабская позиционная система счисления.

- Системы счисления бывают двух видов: позиционные и непозиционные. Чем отличаются позиционная система счисления от непозиционной?

 В позиционной системе счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции, а в непозиционной не зависит.

- Приведите примеры непозиционной системы счисления.

Древнеегипетская десятичная система счисления, римская система счисления.

- Как записываются цифры в римской системе счисления?

В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, то их значения вычитаются.

- Какие цифры используются в данной системе счисления?

Весь материал - в документе.

МОБУ лицей №4

Подготовила: Николаева Светлана Александровна, учитель информатики МОБУ лицей №4

Баймак

Тема: Быстрый перевод чисел.

Цель: - Ознакомить учащихся с правилами быстрого перевода чисел из одной системы счисления в другую; закрепить перевод чисел в десятичную систему счисления и обратно;

- Развить логическое мышление, внимание, память, кругозор учащихся, интерес к предмету;

- Воспитать самостоятельность, аккуратность, ответственность, трудолюбие.

Тип урока: Изучение нового материала.

Ход урока:

1. Организационный момент.

Создание рабочей обстановки в классе.

- Здравствуйте, садитесь.

- Вот уже несколько уроков мы с вами посвятили довольно интересной теме, которая называется «Системы счисления». Сегодня на уроке мы должны еще раз вспомнить все, что касается данной темы, а также рассмотреть новый материал по данной теме.

- Итак, все готовы к работе?

Да.

- Тогда начнем… Для начала давайте поставим перед собой задачи, которые мы должны разрешить в течение нашего урока:

Задача 1. Вспомнить определения понятий, касающихся данной темы, историю систем счисления;

Задача 2. Изучить новый материал;

Задача 3. Закрепить изученный материал;

Задача 4. Выполнить работу за компьютером;

Задача 5. Выполнить гимнастику для глаз и физминутку;

Задача 6. Выполнить самостоятельную работу;

Задача 7. Подвести итоги урока.

1. Повторение изученного материала.

- Что называется системой счисления?

Система счисления – это определенный способ записи чисел и соответствующие ему правила действия над ними.

- А какой системой счисления мы с вами пользуемся в повседневной жизни?

Десятичной.

- Сколько цифр мы используем и что делаем с числами?

Используем 10 цифр, числа складываем и вычитаем поразрядно, умножаем столбиком и делим углом.

- Но вы знаете, что десятичная система счисления не сразу заняла свое господствующее положение, которое занимает сейчас. Раньше многие народы пользовались другими системами счисления. Так довольно широкое распространение имела двенадцатеричная система счисления. Ее происхождение связано со счетом на пальцах руки (кроме большого) имеют 12 фаланг. По ним перебирали большим пальцем и вели счет от 1 до 12. В устной речи остатки 12-ой системы счисления сохранились до сих пор: вместо 12 мы часто говорим дюжина, многие предметы (ножи, вилки, тарелки и т.д.) считают дюжинами, а не десятками. У англичан 1 фунт = 12 дюймов, 1 шиллинг = 12 пенсов.

В древнем Вавилоне широко была распространена шестидесятеричная система счисления, ее происхождение неизвестно, но есть гипотеза, что эта система счисления возникла как компромисс при объединении племен, пользовавшихся шестеричной и десятичной систем счисления. Эта система счисления была громоздкой и неудобной. Кстати, мы до сих пор в счете используем число 60. Что мы считаем по 60?

1 час=60 мин, 1 мин=60 сек, 1⁰=60 ^\, 1^\ = 60 ^\\.

- Верно, итак, кроме рассмотренных систем счисления существовало и множество других систем счисления. Назовите еще несколько систем счисления, которые вы знаете.

А) Единичная система счисления – в записи чисел применялся только один вид знаков – палочка;

Б) Древнеегипетская десятинная непозиционная система счисления – возникла во 2-ой половине третьего тысячелетия до н.э, использовались специальные знаки:

В) Римская система счисления;

Г) Арабская позиционная система счисления.

- Системы счисления бывают двух видов: позиционные и непозиционные. Чем отличаются позиционная система счисления от непозиционной?

В позиционной системе счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции, а в непозиционной не зависит.

- Приведите примеры непозиционной системы счисления.

Древнеегипетская десятичная система счисления, римская система счисления.

- Как записываются цифры в римской системе счисления?

В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, то их значения вычитаются.

- Какие цифры используются в данной системе счисления?

I (1), V (5), X (10), L (50), C (100), D (500), M (1000).

- Хорошо, а сейчас к доске я приглашаю двух желающих для выполнения следующего задания: Выполнить нужно действия в римской системе счисления.

Задание для 1-го ученика:

а) CV – LII = 105 – 52 = 53 = LIII

б) MCM + VIII = 1000 + (-100+1000)+8 = 1908 = MCMVIII

Задание для 2-го ученика:

а) LXVI : XI = (50 + 10 + 6) : 11 = 66 : 11 = 6 = VI

б) XXIV + VII = 24 + 7 = 31 =XXXI

- Пока ребята работают у доски мы с вами выполним следующую работу: у вас на парте находятся знаки, которые использовались при написании цифр в древнеегипетской и вавилонской системах счисления. Вам нужно из этих знаков составить числа:

345 в древнеегипетской системе счисления;

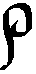
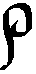
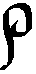
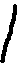
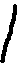
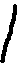
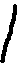
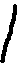
32 в римской системе счисления; XXXII

444 в римской системе счисления. CDXLIV

- Хорошо с непозиционными системами счисления разобрались, а какие позиционные системы счисления вы знаете?

- А какая система счисления используется в компьютере и почему?

В компьютере используется двоичная система счисления, так как в ней все числа записываются при помощи 0 и 1 и устройство компьютера с использованием этой системы счисления будет наиболее простым.

- Правильно, но с ростом числа его двоичная запись увеличивается, к примеру, 8 = 1000₂. Поэтому в компьютере действия производятся в двоичной системе счисления, а хранение и пересылка идет в восьмеричной и шестнадцатеричной системах счислениях. Значит, компьютер должен уметь еще переводить числа из этих систем счисления в двоичную и наоборот. В таких случаях используется быстрый перевод чисел. Рассмотрим его. Запишем тему нашего урока:

1. Изучение нового материала.

Быстрый перевод чисел.

- Давайте вспомним, что мы делали, чтобы перевести число из 10-ой системы счисления в 2-ую, 8-ую, 16-ую системы счисления?

Выполняли алгоритм деления.

- А для того, чтобы перевести число из 2-ой, 8-ой, 16-ой систем счисления в 10-ую систему счисления нужно тоже воспользоваться алгоритмом. Каким?

Алгоритмом умножения.

- Давайте рассмотрим быстрый перевод чисел. Посчитаем вместе, сколько всего случаев у нас будет.

4, из 28, 216,162, 82.

- «28». Этот способ перевода основан на том, что 2³=8.

Разбиваем двоичное число влево и вправо от запятой на триады (по три) и каждую такую группу заменяем соответствующей ей восьмеричной цифрой.

а) 1 ^/ 101₂ = 15₈ (работает у доски учитель, дети помогают)

б) 1 ^/ 101 ^/ 111 ^/010 = 1572₈ (работает ученик у доски)

- «216». Этот способ основан на том, что 2 ⁴ = 16.

Разбиваем двоичное число на тетрады (по четыре) влево и вправо от запятой, затем каждую группу заменяем соответствующей ей шестнадцатеричной цифрой.

а) 1100 ^/ 0010 ^/ 0111 ^/ 0101 ^/ 1111 ^/ 1001₂ = C275F9₁₆ (работает у доски учитель, дети помогают)

б) 1100 ^/ 0010 = С2₁₆ (работает ученик у доски)

- «82». Этот способ основан на том, что 8 = 2³.

Здесь, наоборот, заменяем каждую восьмеричную цифру на соответствующую триаду. Ведущие нули в каждой триаде писать обязательно. В крайней левой триаде ведущие нули можно опустить.

а) 7152₈ = 111 001 101 010₂ (работает у доски учитель, дети помогают)

б) 24₈ = 10 100₂ (работает ученик у доски)

- «162». Этот способ основан на том, что 16 = 2⁴.

Здесь также заменяем каждую шестнадцатеричную цифру на соответствующую тетраду. Ведущие нули в каждой триаде писать обязательно. В крайней левой триаде ведущие нули можно опустить.

а) 35D3₁₆ = 11 0101 1101 0011₂

б) 3A₁₆ = 11 1010₂

1. Закрепление изученного материала.

№1. Перевести двоичные числа в восьмеричную систему счисления:

а) 110000110101=6065₈

б) 0,1111110001=0,7704₈

№2. Перевести двоичные числа в шестнадцатеричную систему счисления:

а) 11011010001=6D1₁₆

б) 0,0110101=0,6A₁₆

№3. Перевести смешанные двоичные числа в восьмеричную и шестнадцатеричную с\с:

а) 100010,011101=42,35₈; 100010,011101=22,74₁₆

б) 100011,1111=43,74₈; 100010,011101=23,F₁₆

№4. Перевести восьмеричные числа в двоичную с\с:

а) 256=10 101 110₂

б) 24,025=10 100, 000 010 101₂

№5. Перевести шестнадцатеричные числа в двоичную с\с:

а) 1AC7 = 1 1010 1100 0111₂

б) 2F,D8C = 10 1111, 1101 1000 1100₂

№6. Перевести числа из шестнадцатеричной с\с в восьмеричную с\с:

а) A45 = 101 001 000 101₂ = 5105₈

б) F12,0457 = 1111 0001 0010, 0000 0100 0101 0111₂ = 7422,010534₈

1. Практическая работа за компьютером.

Задание. В какой системе счисления происходили действия в данной истории? Переделайте историю так, чтобы все действия происходили в восьмеричной системе счисления.

На кресле толстый кот Мартын сидел,

Своими 10 глазами он смотрел,

Вдруг на 100 своих он лап вскочил,

На подоконник быстро тело приземлил.

Увидел он 1010 воробьев,

Но вот своей он 100-й лапой

Задел горшочек с маминым цветком,

И, боже, что было бы потом,

Если бы кот не убежал оттуда,

Не сел на кресло и не стал чесать

За своим 10-м маленьким ушком.

Ведь обвинили во всем меня,

А кот Мартын лежал на кресле,

Весело мурча!

1. Упражнение для глаз.

   1. Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до пяти. Повторить 4 – 5 раз.

   2. Крепко зажмурить глаза (считать до трех), открыть их и посмотреть вдаль (считая до пяти). Повторить 4 – 5 раз.

   3. Вытянуть правую руку вперед. Следить глазами, не поворачивая головы, за медленным движением указательного пальца вытянутой руки влево и вправо, вверх и вниз. Повторить 4 – 5 раз.

   4. В среднем темпе проделать 3 – 4 круговых движения глазами в правую сторону, столько же в левую сторону. Расслабив глазные мышцы, посмотреть вдаль на счет 1 – 6. Повторить 1 - 2 раза.

1. Самостоятельная работа.

Задание: В таблице представлены числа, записанные в различных системах счисления. По данной таблице подсчитать:

1. Сумму чисел в каждой строке;

2. Произведение чисел в столбцах.

Вариант 1

2 вариант

1. Дополнительно.

Задание. Разгадать кроссворд:

Вариант 1

По горизонтали:

а)1110+1101

в)2440₈=…₁₀

г)1095=…₈

д)110001-11000

По вертикали:

а)23=…₂

б)111∙11

Вариант 2

По горизонтали:

а)1110+1011

в)4417₈.=…₁₀

г)542=…₈

д)110110-11011

По вертикали:

а)21=…₂

б)101·101

1. Подведение итогов урока и постановка домашнего задания.

- Что нового мы с вами узнали на уроке?

- С какими числами работает компьютер?

- Для чего нужно знать правила быстрого перевода чисел?

- А теперь давайте запишем домашнее задание.

Задание: Выучить правила быстрого перевода чисел. Перевести следующие числа:

1. ABC,1A₁₆  ?₈; ABC,1A₁₆  ?₂

2. 123,56₈  ?₁₆; 123,56₈  ?₁₆

3. 101011,101₂  ?₈; 101011,101₂  ?₁₆

4. 456,7₈  ?₁₆; 456,7₁₆  ?₈

(Оценить работу учащихся.)

- Урок окончен, до свидания. Рабочее место приведите в порядок.

Раздаточный материал

Задачи

№1. Перевести двоичные числа в восьмеричную систему счисления:

а) 110000110101

б) 0,1111110001

№2. Перевести двоичные числа в шестнадцатеричную систему счисления:

а) 11011010001

б) 0,0110101

№3. Перевести смешанные двоичные числа в восьмеричную и шестнадцатеричную с\с:

а) 100010,011101

б) 100011,1111

№4. Перевести восьмеричные числа в двоичную с\с:

а) 256

б) 24,025

№5. Перевести шестнадцатеричные числа в двоичную с\с:

а) 1AC7

б) 2F,D8C

№6. Перевести числа из шестнадцатеричной с\с в восьмеричную с\с:

а) A45

б) F12,0457

№7. Перевести следующие числа:

1. 23₁₆  ?₂; 23,45₈  ?₂

1010,0011101₂  ?₈; 1010,0011101₂  ?₁₆

1. AC1₁₆  ?₈; 101010₈  ?₂

101010₂  ?₈; 23,561₈  ?₁₆

№8. Перевести следующие числа:

1. 10101,01₂  ?₈; 10101,01₈  ?₁₆

10101,01₁₆ ?₈; 10101,01₈  ?₂

1. 11001,11₂  ?₈; 11001,11₈  ?₁₆

11001,11₁₆  ?₈; 11001,11₈  ?₂

Вариант 1

По горизонтали:

а)1110+1101

в)2440₈=…₁₀

г)1095=…₈

д)110001-11000

По вертикали:

а)23=…₂

б)111∙11

Вариант 2

По горизонтали:

а)1110+1011

в)4417₈.=…₁₀

г)542=…₈

д)110110-11011

По вертикали:

а)21=…₂

б)101·101

Вариант 1

По горизонтали:

а)1110+1101

в)2440₈=…₁₀

г)1095=…₈

д)110001-11000

По вертикали:

а)23=…₂

б)111∙11

Вариант 2

По горизонтали:

а)1110+1011

в)4417₈.=…₁₀

г)542=…₈

д)110110-11011

По вертикали:

а)21=…₂

б)101·101

Вариант 1

2 вариант

15