Цели урока:
Образовательные:
ввести определение квадратного уравнения;
ввести понятие коэффициент квадратного уравнения;
ввести определение неполного квадратного уравнения;
научить решать неполные квадратные уравнения
закрепить и систематизировать полученные знания в ходе выполнения упражнений;
Воспитательные:
воспитывать умение отстаивать свои взгляды
воспитывать настойчивость в достижении своей цели
воспитывать информационную культуру.
Развивающие:
развивать критическое мышление
развивать познавательные процессы (внимание, память, восприятие)
Развивать интерес к самостоятельному добыванию знаний.
Тип урока Урок усвоения новых знаний
Ход урока
Организационный момент. Постановка темы и цели урока.
Сегодня на уроке мы начинаем изучение новой главы, которая называется
«Квадратные уравнения». В ходе изучения главы мы должны:
- научиться выделять квадратные уравнения;
- определять их вид;
- уметь решать их.
Вопросы.
Что значит решить уравнение? (Найти его корни, или показать, что корней нет.)
Что называется корнем уравнения? (Значение переменной при котором уравнение превращается в верное равенство.)
Ребята, на уроке будем работать в парах, это позволит вам обсудить спорные вопросы или что-то непонятное спросить у соседа.
На каждом столе лежат листы с заданиями:
Рабочий лист, на котором записываем все свои рассуждения и решения. Его необходимо подписать (Ф.И. на первой строке, на второй тема урока).
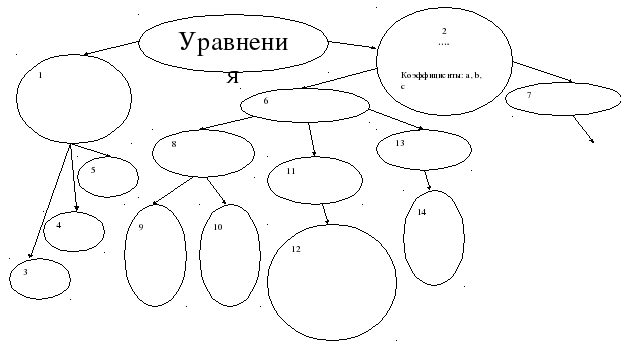
Внутри листа находится схема кластер, который заполняется в течение нескольких уроков (см приложение 1)
Синий лист, на котором записаны уравнения, они записаны на доске
(см. приложение 2)
Белый лист, на нем записаны задания которые мы выполним в конце урока
(см. приложение 3)
Ваша работа на уроке будет оценена. В течение урока вы будете получать «+», затем мы их посчитаем и по их количеству выставим оценку:
«5» - 11-12
«4» - 9-10
«3» - 7-8
Актуализация.
Вопросы.
Какие уравнения мы, с вами, умеем решать? (Линейные - №1)
Какое уравнение называется линейным?
(Уравнение вида ах = в, где …).
Обсудить в парах, записать в ячейку, проверить, поставить «+».
Сколько корней может иметь линейное уравнение?
Обсудить в парах 1 мин., выслушать несколько ответов и записать в ячейки. (Один корень - №3, Много корней – №4, или не иметь - №5)
При каких условиях? Обсудить в парах 1 мин., выслушать несколько ответов и записать в соответствующую ячейку.
Задание №1: (синий лист) Выберите из предложенных уравнений ЛИНЕЙНЫЕ и запишите их номера (1, 5, 10) и решите. К доске вызвать по одному ученику и проверить с классом поднятием руки. Если верно поставить «+»
№1. 5х = 60, 5х – 150 = 0, -9х = -3,
х = 60 : 5, 5х = 150, х = -3: (-9),
х = -12. х = 30. х = -1/9.
Ответ: -12. Ответ: 30. Ответ: -1/9
3. Изучение новой темы.
На доске остались уравнения.
Вопросы.
Чем отличаются оставшиеся уравнения?
(В этих уравнениях содержится переменная во второй степени)
Действительно, каждое из оставшихся уравнений содержит переменную во второй степени. Такие уравнения называются КВАДРАТНЫМИ. Запишите в ячейку №2.
Кто может сформулировать определение?
Обсудить в парах 1 мин., выслушать несколько ответов, проверить себя.
Задание №2: Откройте учебник на стр.44 и прочитайте 5, 6,7 абз.
Какие же уравнения называются квадратными?
(Уравнение вида ах2 + вх + с = 0 где х – переменная, а, в, с - …, а ≠ 0) Записать в ячейку №2. Если верно поставить «+».
Все ли уравнения имеют вид ах2 + вх + с = 0? (Нет).
Задание №3: Выпишите номера только тех уравнений, которые имеют вид квадратных (2, 7, 11)
Можно ли оставшиеся уравнения назвать квадратными? (Можно, только они неполные)
Действительно квадратные уравнения можно разбить на две группы: неполные - №6, полные - №7. Запишите в ячейки.
Решение полных квадратных уравнений мы рассмотрим на одном из следующих уроков. А сегодня мы должны научиться решать неполные квадратные уравнения, объяснить почему они называются неполными, и сколько корней может иметь неполное квадратное уравнение.
Как вы думаете, почему эти уравнения назвали неполными? Обсудить в парах 1 мин. Выслушать предполагаемые ответы, записать их на доске.
Задание №4: справьте неверные ответы.
Поставьте «+», если верно.
в = 0, с = 0 с = 0, в ≠ 0 в = 0, с = 0
ах2 + с = 0 ах2 + вх = 0 ах2 = 0
Задание №5: Разбейте уравнения на три группы и запишите их номера
1 гр. – 3, 8
2 гр. – 6, 12
3 гр. – 4, 9
Проверить поднятием руки. Поставить «+», если верно.
Задание №6: Решите уравнения 1гр. (Кто первый решает на месте выходит к доске); проверяем вместе с классом и ставим «+»
3х2 – 12 = 0, 4х2 + 8 = 0,
3х2 = 12, 4х2 = - 8,
х2 = 12 :3 х2 = - 8 : 4,
х2 = 4 х2 = - 2
х = 2 или х = -2. не имеет смысла
Ответ: -2, 2 Ответ:
На примере решения данных уравнений, мы видим, что уравнение такого вида, может иметь либо 2 корня, либо не иметь корней. Запишите в ячейки №9, №10.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Неполные квадратные уравнения (72.5 КB)
Неполные квадратные уравнения (72.5 КB)
 0
0 758
758 68
68 Нравится
0
Нравится
0









