Цель урока: Рассмотреть новый тип уравнения, сформировать умения и навыки решения неполных квадратных уравнений.
Задачи: Способствовать проявлению результатов труда каждого учащегося, развивать умение оценивать свой труд и труд товарищей.
1 минимодуль
2 минуты – организационный момент, мотивация.
Задача. Площадь прямоугольника равна 112 см², его ширина на 6 см меньше длины. Найти стороны прямоугольника.
Предложите способ решения задачи.
Верно, необходимо составить уравнение
Решение.
Пусть ширина прямоугольника равна х см, тогда его длина будет (х+6) см. Площадь равна 112 см. Следовательно, имеем уравнение х(х+6) =112, то есть х² + 6х = 112, или
х² + 6х – 112 = 0
Имеем уравнение с одной переменной и переменная эта во второй степени, то есть в квадрате, а значит и уравнение мы назовем квадратным.
Квадратное уравнение – это уравнение вида ах² + вх + с = 0, где а≠0 , х- переменная, а,в,с- данные числа: а- первый (старший) коэффициент, в – второй коэффициент, с – свободный член.
По определению а≠0, почему?
Если хотя бы один из коэффициентов в или с равен нулю, уравнение называют неполным.
Какие возможны варианты, какой вид будут при этом иметь неполные уравнения?
Вместе попробуем найти алгоритм решения неполного уравнения и определим количество корней каждого из них. Предлагаю вам самостоятельно придумать соответствующие примеры.
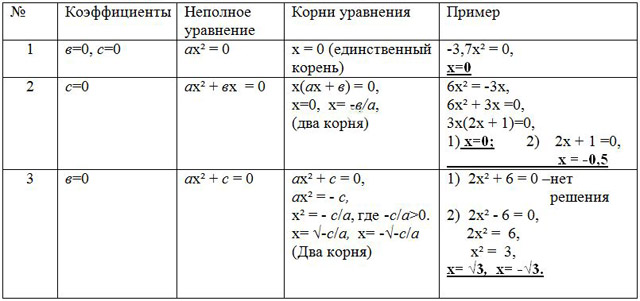
Для закрепления материала (устно): № № 861-866 (фронтальный опрос).
Какое из данных уравнений квадратное:
а) х²=1/х + 3; б) -2х² + 3х = 4; в) х² +5х -0.7 = 0; г) 2х² + х³ = 0; д) 5х² = 5х – 3; е) 2х(х + 5) = 7 ?
Какое из данных уравнений неполное квадратное:
а) х² + 3 = 0; б) -2х² = 0; в) х² +5х = 1; г) 2х² + 2/х = 0; д) 5х² + πх = 0; е) 2х² +√х = 0 ?
Решите уравнения:
а) 3х² = 0; б) √7·х = 0; в) -х² = 0;
г) х² - 2 х = 0; д) 3х² - 6х = 0; е) 2х² = х ?
ж) х² - 9 = 0; з) 2х² - 8 = 0; и) -х² + 1 = 0;
к) (х-1)(х-5) = 0; л) 3(х+7)(х-6) = 0; м) (2х – 1)(х+3) = 0?
Заканчиваются первые 30 минут.
Продолжите предложение: Только что я узнал… (понял, разобрался…)
2 минимодуль
Вторую тридцатиминутку мы посвящаем решению неполных квадратных уравнений, а также уравнений, которые к ним приводятся.
№ 867. Выпишите из данных уравнений:
а) квадратные уравнения;
б) неполные квадратные уравнения.
Приведите их к стандартному виду и для каждого из них укажите, чему равны его первый и второй коэффициенты и свободный член. (Работа у доски)
а) 3х-7=х²; б) -2х² + √3·х = 4; в) 6х² - х³ = 0 г) (х+4)² = 8х;
д) 0,3 х² + 2х = 0; е) х + 1/х + 4 = 0; ж) 9х² = 0; з) х² - 25 = х.
Решите уравнение:
№№ 870-872. Трое учащихся решают по три разнотипных уравнения, по очереди комментируя. Рецензия и оценивание решения (трое сильных учеников, закрепленные за каждым из отвечающих, следят за правильностью решения ).
1) 16х² = 0 1) - 4х² = 0 1) (√7 +√3)х² = 0
2) 2х² - 6х = 0 2) х² + 3х = 0 2) 7х² = 0,5х
3) -2х² + 50 = 0 3) 0,16х² + 100 = 0 3) х² + 16² = 65²
№ 877, 888
1) 2(х² -1) – (х-1)(х+1); 2) (х + 3)² = (х – 3)(х + 3);
3) (5 – х²)/3 = (3х² -2)/4; 4) (2х²)/5 = (3х² + 1)/4 .
Итак, дорогие ребята, ещё раз повторяем алгоритм решения каждого типа неполных квадратных уравнений…
3 минимодуль
Эти 30 минут мы решаем с вами, во первых, задачи на составление уравнений, а во вторых выполним небольшую самостоятельную работу на закрепление изученного материала.
Решить задачи.
№ 902. Найдите длины катетов прямоугольного равнобедренного треугольника, площадь которого равна 0,72 дм².
№ 904. Площадь кольца равна 942 см², радиус его внешнего круга – 20 см. Найдите радиус внутреннего круга.
Самостоятельная работа.
Вариант 1 Вариант 2
1) -79х² = 0; 1) - 74х² = 0;
2) 7х² + 5х = 0; 2) 9х² + 7х = 0;
3) -4х² + 100 = 0; 3) -16х² + 64 = 0;
4) 5х² + 3х +7 = 7(х + 1); 4) 15 – 2х = 8х² + 3(х + 5;
5) 3х(х – 1) = 12 – 3х. 5) 5х(х + 2) = 10 (1 + х).
Уважаемые ребята, мы с вами сегодня славно потрудились.
Что было сложного и непонятного?
Чему мы с вами сегодня научились?
Учитель комментирует работу учащихся и ставит оценки.
Запишите домашнее задание. § 19 – изучить, выполнить №№ 868, 869, 876.
Успехов вам.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Неполные квадратные уравнения (49 КB)
Неполные квадратные уравнения (49 КB)
 0
0 1647
1647 262
262 Нравится
0
Нравится
0








