Разработка урока
по алгебре
для 8-х классов по теме:
«Квадратные уравнения.
Решение неполных квадратных уравнений»
Подготовила
учитель
Перевальской гимназии № 1
Левченко И. А.
Цели урока: – формирование знаний учащихся о способах решения неполных квадратных уравнений в зависимости от вида неполного квадратного уравнения;
– развитие умений сравнивать, выявлять закономерности, обобщать;
– развитие навыков самоконтроля;
– воспитание воли и настойчивости для достижения конечных результатов при решении неполных квадратных уравнений.
Тип урока: урок изучения нового материала.
Оборудование:
– таблицы с формулами сокращенного умножения;
– раздаточный материал.
Структура урока:
– организационный момент;
– постановка цели урока;
– ознакомление с новым материалом;
– подведение итогов урока;
– постановка домашнего задания.
Ход урока:
Организационный момент
Система заданий для актуализации опорных знаний
1. Сформулируйте определение квадратного уравнения.
2. Как называются числа a, b и c в уравнении ax² + bx + c = 0?
3. Сколько существует видов неполных квадратных уравнений?
4. Сформулируйте определение неполного квадратного уравнения.
5. Всегда ли квадратные уравнения имеет корни? Приведите примеры.
II. Постановка цели урока.
Сегодня на уроке мы продолжим изучение темы «Неполные квадратные уравнения». На предыдущем уроке мы с вами познакомились с видами неполных квадратных уравнений, научились преобразовывать уравнения и приводить к квадратным. Целью сегодняшнего нашего урока будет научиться решать неполные квадратные уравнения. А делать это вы будете с помощью учебных упражнений, в которых дается описание способа решения того или иного вида неполного квадратного уравнения, а также задания для самостоятельной работы. Учебные упражнения поделены на три уровня:
I-й уровня – содержит обязательный минимум, который должны выполнить все учащиеся (обеспечивает при правильном выполнении оценку «6»);
II-й уровень – задания представлены в усложненном виде (обеспечивает при правильном выполнении оценку «9»);
III-й уровень – задания представлены в нестандартном виде и требуют большей подготовленности (обеспечивает при правильном выполнении оценку «12»);
Учебные упражнения с 1-го по 4-й представляет собой I-й уровень сложности, упражнение №5 – II-й уровень сложности, упражнение №6 – III-й уровень сложности.
Ответы и критерии оценивания находятся у учителя.
Ознакомление с новым материалом.
Каждый учащийся получает упражнение, читает указания учителя и выполняет самостоятельную работу. После чего сверяет свои ответы и ставит набранное количество баллов в оценочный лист. После того, как учащийся набирает необходимое количество баллов, приступает к выполнению следующих учебных упражнений.
Подведение итогов.
Учащиеся подводят итоги своей работы, оценивая самостоятельно согласно набранным баллам. Оценки выставляются в журнал.
Домашнее задание
Выполнить следующие задания:
а) устно – прочесть §19 учебника «Алгебра – 8» (Г.П. Бевз, В.Г. Бевз)
б) письменно – № 879, 886, 890.
Приложения
Упражнение №1
Цель: закрепить умения решать уравнения вида х² = а.
Указания учителя
Вспомните правила решения уравнения х² =а. Для этого прочитайте пояснения, данные ниже.
Рассмотрите уравнение х² = а, где а – произвольное число. В зависимости от числа а при решении этого уравнения возможны три случая.
Если а² = а корней не имеет. Действительно, не существует числа, квадрат которого был бы равен отрицательному числу.
Если а=0, то уравнение имеет один корень, равный нулю.
Если а0, то уравнение имеет два корня: 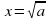 и
и 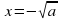 .
.
Выполнить письменно самостоятельную работу.
Задание для самостоятельной работы
I вариант II вариант
1) х² = 81 (1 балл) 1) х² = 36 (1 балл)
2) х² = 0 (1 балл) 2) х² = 0 (1 балл)
3) х² = –36 (1 балл) 3) х² = –25 (1 балл)
Указание учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 3 балла, то переходите к следующему учебному упражнению. Если же набрали меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Упражнение №2
Цель: научить учащихся решать уравнения вида ах² = 0.
Указания учителя
Прочитайте данные ниже пояснения.
Неполные квадратные уравнения вида ах² = 0, равносильно х² = 0 и поэтому имеет единственный корень, равный нулю.
Пример. Решить уравнение 4х² = 0.
Решение. Так как уравнение вида ах² = 0, равносильно х² = 0, то
4х² = 0
х² = 0
х = 0
Ответ: х = 0.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
I вариант II вариант
1) 5х² = 0 (1 балл) 1) 14х² = 0 (1 балл)
2) –8х² = 0 (1 балл) 2) –7х² = 0 (1 балл)
3) 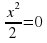 (2 балла) 3)
(2 балла) 3) 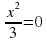 (2 балла)
(2 балла)
Указание учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 3 баллов и более, то переходите к следующему учебному упражнению. Если же набрали меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Упражнение №3
Цель: научить учащихся решать уравнения вида ах² + с = 0, где с ≠ 0.
Указания учителя
Прочитайте данные ниже пояснения.
Для решения неполные квадратные уравнения вида ах² + с = 0, где с ≠ 0 переносят его свободный член в правую часть и делят обе части уравнения на а. Получают уравнение 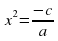 , равносильноe уравнению вида ах² + с = 0.
, равносильноe уравнению вида ах² + с = 0.
Так как с ≠ 0, то 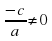 .
.
Если 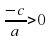 , то уравнение имеет два корня:
, то уравнение имеет два корня: 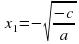 и
и 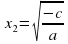
Если 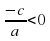 , то уравнение не имеет корней.
, то уравнение не имеет корней.
Пример. Решить уравнение 4х² + 3 = 0.
Решение. Перенесем свободный член в правую часть уравнения и обе части получившегося уравнения разделим на 4:
4х² = –3,
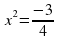 .
.
Так как квадрат числа не может быть отрицательным числом, то получившееся уравнение не имеет корней. А, следовательно, не имеет корней и равносильное ему уравнение 4х² + 3 = 0.
Ответ: корней нет.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
I вариант II вариант
1) 2х² – 18 = 0 (2 балла) 1) 4х² – 9 = 0 (2 балла)
2) –0,2х² + 20 = 0 (2 балла) 2) – 0,1х² + 10 = 0 (2 балла)
3) 3х² + 12 = 0 (3 балла) 3) 6х² + 24 = 0 (3 балла)
Указание учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов и более, то переходите к следующему учебному упражнению. Если же набрали меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Упражнение №4
Цель: научить учащихся решать уравнения вида ах² + bх = 0, где b ≠ 0.
Указания учителя
Прочитайте данные ниже пояснения.
Для решения неполных квадратных уравнений вида ах² + bх = 0, где b ≠ 0, раскладывают его левую часть на множители и получают уравнение
х(ах + b) = 0.
Произведение х(ах + b) равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
х = 0 или (ах + b) = 0.
Решая уравнение (ах + b) = 0, в котором а ≠ 0, находим: ах = –b,
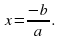
Следовательно, произведение х(ах + b) обращается в нуль при х = 0 и при 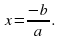
Корнями уравнения х(ах + b) являются числа 0 и 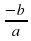 .
.
Значит, неполное квадратное уравнение вида ах² + bх = 0, где b ≠ 0 всегда имеет два корня.
Пример. Решить уравнение 4х² + 9х = 0.
Решение. Разложим левую часть уравнения на множители:
х(4х + 9) = 0.
Отсюда х = 0 или 4х + 9 = 0.
Решим уравнение 4х + 9 = 0:
4х = –9
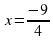
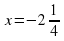 .
.
Ответ: х = 0, х = 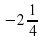 .
.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
I вариант II вариант
1) 2х² – 3х = 0 (2 балла) 1) 3х² – 4х = 0 (2 балла)
2) –14х² + 7х = 0 (3 балла) 2) –5х² + 6х = 0 (3 балла)
Указание учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов, то переходите к следующему учебному упражнению. Если же набрали меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Упражнение №5
Цель: закрепить умение учащихся решать неполные квадратные уравнения; проверить умения учащихся выбирать способ решения неполных квадратных уравнений в усложненных заданиях.
Указания учителя
Вы прошли I уровень усвоения материала. Теперь вы самостоятельно выбираете способ решения неполных квадратных уравнений в предложенных заданиях. Для этого вспомните все способы решения неполных квадратных уравнений, пройденных в 1-4 учебных упражнениях.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
I вариант II вариант
1) 2 = 7х² + 2 (2 балла) 1) 9х² – 1 = –1 (2 балла)
2) 2х² = 3х (2 балла) 2) 3х² = –2х (2 балла)
3) 4х² – 11 = х² – 11 + 9х (3 балла) 3) 7х² + 3 = 2х² + 15х + 3 (3 балла)
Указание учителя
Список правильных ответов и критерии оценивания возьмите у учителя. Исправьте ошибки, если они есть. Число набранных баллов поставьте в графу «Основные задания» оценочного листа. Если вы набрали 5 баллов и более, то переходите к следующему учебному упражнению. Если же набрали меньше баллов, то решите задания другого варианта, аналогичные тем, в которых была допущена ошибка. Набранные баллы поставьте в графу «Корректирующие задания».
Упражнение №6
Цель: проверить знания и умения учащихся решать неполные квадратные уравнения в предложенных заданиях.
Указания учителя
Молодцы! Вы освоили решение неполных квадратных уравнений II уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умение при решении неполных квадратных уравнений в более сложных заданиях.
Выполните письменно самостоятельную работу.
Задания для самостоятельной работы
(х – 1)(х + 1) = 2х – 1 (2 балла)
(х + 3)(х – 4) = –12 (2 балла)
(2х – 1)² – 1 = 0 (3 балла)
Указание учителя
В случае затруднений воспользуйтесь подсказками, данными ниже.
1) Воспользуйтесь формулой сокращенного умножения: а² – b² = (а – b)(а + b).
2) Перемножьте скобки, приведите подобные слагаемые.
3) Воспользуйтесь формулой сокращенного умножения: (а – b)= а² – 2аb + b².
Проверьте и оцените свои работы.
Если вы набрали 31 – 32 баллов, вы получаете оценку 12,
29 – 30 баллов – 11, 16 – 17 баллов – 6,
26 – 28 баллов – 10, 13 – 15 баллов – 5,
23 – 25 баллов – 9, 10 – 12 баллов – 4,
20 – 22 баллов – 8, 6 – 9 баллов – 3,
18 – 19 баллов – 7, 1 – 5 баллов – 2.

 Получите свидетельство
Получите свидетельство Вход
Вход



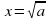 и
и 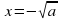 .
.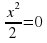 (2 балла) 3)
(2 балла) 3) 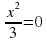 (2 балла)
(2 балла)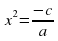 , равносильноe уравнению вида ах² + с = 0.
, равносильноe уравнению вида ах² + с = 0.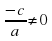 .
.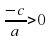 , то уравнение имеет два корня:
, то уравнение имеет два корня: 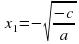 и
и 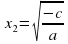
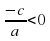 , то уравнение не имеет корней.
, то уравнение не имеет корней.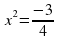 .
.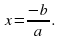
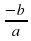 .
.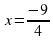
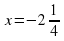 .
.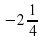 .
.








 Разработка урока математики «Квадратные уравнения. Решение неполных квадратных уравнений» (29.26 КB)
Разработка урока математики «Квадратные уравнения. Решение неполных квадратных уравнений» (29.26 КB)
 0
0 589
589 60
60 Нравится
0
Нравится
0


