Получите свидетельство
Вход
23.09.19
Классная работа
Наибольший общий делитель
Найдем все делители чисел 54 и 36 .
делится на
делится на
Общими делителями являются числа:
1, 2, 3, 6, 9, 18.
Значит из купленных цветов можно составить 1, 2, 3, 6, 9 или 18 букетов.
Наибольшее количество
букетов – 18 .
Разложим числа на простые множители:
54 2 36 2 54 = 2 * 3 * 3 *3
27 3 18 2
9 3 9 3 36 = 2 * 2 * 3 * 3
3 3 3 3
1 1
Вычеркнем из разложения первого числа множители, которых нет в разложении второго.
54 = 2 * 3 * 3 * 3
36 = 2 * 2 * 3 * 3
Оставшиеся множители перемножим.
Итак,
НОД(54, 36) = 2 * 3 * 3 = 18.
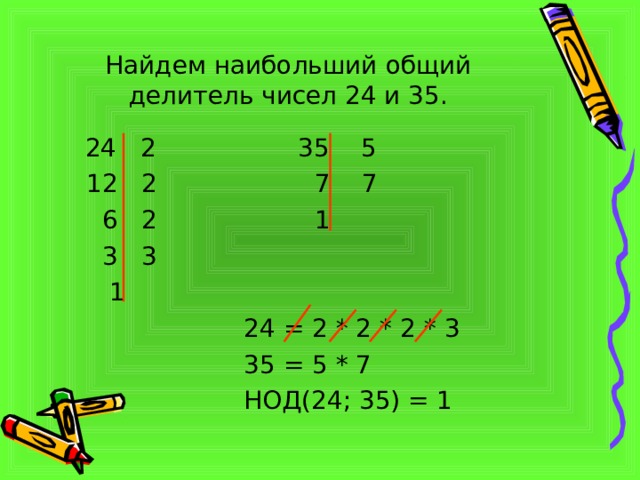
Найдем наибольший общий делитель чисел 24 и 35.
24 2 35 5
12 2 7 7
6 2 1
3 3
1
24 = 2 * 2 * 2 * 3
35 = 5 * 7
НОД(24; 35) = 1
Определение.
Числа, наибольший общий делитель которых равен 1, называются взаимно простыми
Закрепление.
№ 146
Домашнее задание:
п. 6, № 169, 170(а), 172, повт. № 162
Спасибо за урок!
"Наибольший общий делитель" (205 KB)
0
330
19
Нравится
0
