Наибольший общий делитель

Ход урока:

Добрый день, ребята! На предыдущих уроках вы уже знакомились с понятием наибольшего общего делителя нескольких натуральных чисел, а также знаете, что, если числитель и знаменатель дроби делить на наибольший общий для них делитель, то получается уже несократимая дробь. Почему же мы снова возвращаемся сегодня к этому понятию? Дело в том, что для отыскания НОД удобно использовать разложения чисел на простые множители, которые  мы выполняли на предыдущих уроках. Итак, цель урока – освоить правило отыскания НОД с помощью разложения чисел на простые множители.

Давайте вспомним основные понятия и метод, которым мы ранее находили НОД натуральных чисел.

Определение: Делителем натурального числа a называют натуральное число b, на которое a делится без остатка.

Так, делители числа 12: 1, 2, 3, 4, 6, 12.

Выполним самостоятельно следующее задание:

Найти все делители 45.

Найти все делители 60.

Найти все общие делители чисел 45 и 60.

Найти наибольший общий делитель чисел  45 и 60.

А теперь проверим себя:

Делители 45: 1, 3, 5, 9, 15, 45.

Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Общие делители: 1, 3, 5, 15.

НОД (45, 60) = 15.

Такой  способ поиска всех делителей чисел, а затем выбор из них наибольшего общего делителя  для данных чисел, может оказаться долгим и затруднительным, так как связан с подбором большого количества делителей, и есть риск какой-то из них при этом потерять, который как раз и может являться наибольшим общим делителем. Поэтому сегодня мы познакомимся с другим способом отыскания НОД.

Еще немного теории:

Пример: 2, 3, 5, 7, 11, 13 и так далее.

Пример: 4, 6, 8, 9, 10, 12 и так далее.

«Простые числа – это «кирпичики», из которых строятся остальные натуральные числа».

Представление числа в виде произведения степеней простых чисел называют  разложением числа на простые множители.

Выполним самостоятельно следующее задание:

Разложить на простые множители числа 48 и 63.

Найти ошибку в разложении числа на простые множители:

560 = 2³ ·7 · 10.

Урок математики в 6 классе по теме: « Наибольший общий делитель»

Разработан учителем математики

высшей категории Николаевской средней школы Ростовской области

Кривенко Натальей Николаевной

Добрый день, ребята! На предыдущих уроках вы уже знакомились с понятием наибольшего общего делителя нескольких натуральных чисел, а также знаете, что, если числитель и знаменатель дроби делить на наибольший общий для них делитель, то получается уже несократимая дробь. Почему же мы снова возвращаемся сегодня к этому понятию? Дело в том, что для отыскания НОД удобно использовать разложения чисел на простые множители, которые мы выполняли на предыдущих уроках. Итак, цель урока – освоить правило отыскания НОД с помощью разложения чисел на простые множители. Давайте вспомним основные понятия и метод, которым мы ранее находили НОД натуральных чисел.

Определение:

Делителем натурального числа a называют натуральное число b, на которое a делится без остатка.

Так, делители числа 12: 1, 2, 3, 4, 6, 12.

Выполним самостоятельно следующее задание:

• Найти все делители 45 .
• Найти все делители 60 .
• Найти все общие делители чисел 45 и 60 .
• Найти наибольший общий делитель чисел 45 и 60.

А теперь проверим себя:

• Делители 45: 1, 3, 5, 9, 15 , 45.
• Делители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15 , 20, 30, 60.
• Общие делители: 1, 3, 5, 15.
• НОД (45, 60) = 15.

Такой способ поиска всех делителей чисел, а затем выбор из них наибольшего общего делителя для данных чисел, может оказаться долгим и затруднительным, так как связан с подбором большого количества делителей, и есть риск какой-то из них при этом потерять, который как раз и может являться наибольшим общим делителем. Поэтому сегодня мы познакомимся с другим способом отыскания НОД.

Еще немного теории:

• Натуральные числа, имеющие только два делителя, называют простыми .

Пример : 2, 3, 5, 7, 11, 13 и так далее.

• Натуральные числа, имеющие более двух делителей, называют составными .

Пример : 4, 6, 8, 9, 10, 12 и так далее.

«Простые числа – это «кирпичики», из которых строятся остальные натуральные числа».

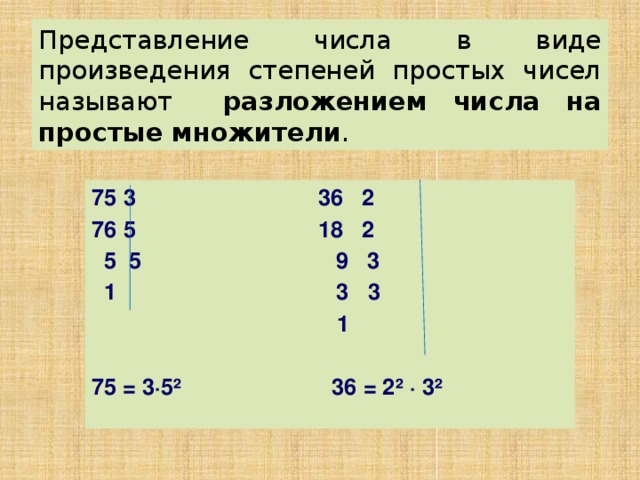
Представление числа в виде произведения степеней простых чисел называют разложением числа на простые множители .

• 3 36 2

• 5 18 2

5 5 9 3

1 3 3

1

75 = 3·5² 36 = 2² · 3²

Выполним самостоятельно следующее задание:

• Разложить на простые множители числа 48 и 63.
• Найти ошибку в разложении числа на простые множители:

560 = 2³ ·7 · 10

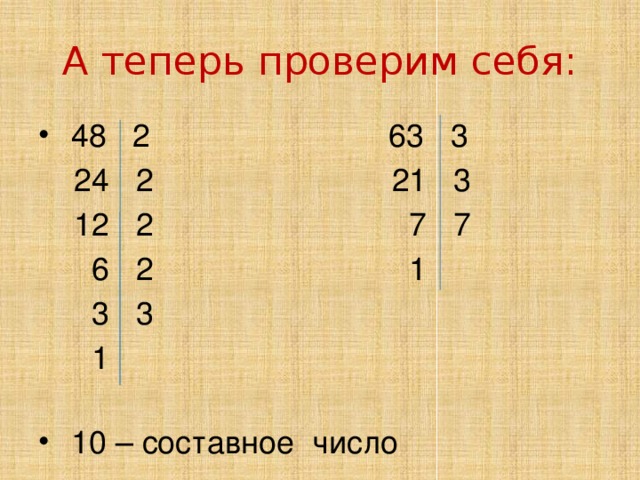
А теперь проверим себя:

• 48 2 63 3

24 2 21 3

12 2 7 7

6 2 1

3 3

1

• 10 – составное число

Итак, теперь мы готовы идти дальше. Напомню цель урока – научиться использовать разложение чисел на простые множители для отыскания НОД чисел.

Задачи:

• Разложить на простые множители числа, разложить их НОД на простые множители, проанализировать полученные результаты.
• На основании полученных результатов сформулировать правило отыскания НОД.
• С помощью правила научиться находить НОД чисел.

Для решения первой поставленной задачи выполним задание:

1) Найти НОД(12; 18), НОД(40; 100);

2) Каждую пару чисел и их НОД разложите на простые множители. Какая связь между разложениями на простые множители чисел и их НОД?

А теперь попробуйте сформулировать правило отыскания НОД!

Итак, правило отыскания НОД:

• Разложить данные числа на простые множители.
• Выписать все простые числа, которые одновременно входят в каждое из полученных разложений.
• Каждое из выписанных простых чисел взять с наименьшим из показателей степени, с которыми оно входит в разложения данных чисел.
• Записать произведение полученных степеней.

Ну, а теперь, нам осталось справиться с последней поставленной на сегодняшнем уроке задачей – с помощью правила находить НОД чисел, и цель урока будет достигнута. Для этого вместе выполним задание – найти НОД чисел: 1) 350 и 756; 2) 405 и 847; 3) 189 и 875; А теперь сократим дроби: 1) 350 756 2) 405 847 3) 189 875 МОЛОДЦЫ!

Подведем итоги: 1) Как вы понимаете утверждение: а – делитель b? 2) Какие числа называют простыми, а какие – составными? 3) Объясните, как найти НОД чисел. 4) Как нахождение НОД чисел связано с сокращением дробей? 5) Как вы считаете, поставленная цель достигнута нами сегодня на уроке? Если нет, то что нам еще нужно сделать, чтобы ее достичь? Спасибо за работу!

Заключение Хочу завершить наш урок следующими заметками:

Раздел математики, в котором изучаются свойства чисел и действий над ними, называют теорией чисел . Начало создания теории чисел положили древнегреческие ученые Пифагор, Евклид, Эратосфен и другие.

Ф. Энгельс : «Как понятие числа, так и понятие фигуры заимствованы исключительно из внешнего мира, а не возникли в голове из чистого мышления».

Литература и информационные ресурсы:

• Учебник «Математика 6 класс», авторы И. И. Зубарева, А. Г. Мордкович;
• Интернет-ресурсы («Яндекс картинки »).