Наибольшее и наименьшее значение функции

Наибольшее и наименьшее значения функции. Четные и нечетные функции.

Задачи урока:

• Актуализировать знания о функции и ее свойствах;
• Узнать и понять: наибольшее и наименьшее значения функции, четная и нечетная функция;
• Закрепить данные понятия на практике.

Актуализация знаний

• Что называется:

• функцией; (стр. 331)
• Областью определения и множеством значения функции;

• Какие способы задания функции существуют?
• Что называется графиком функции?
• Какими свойствами обладает функция?

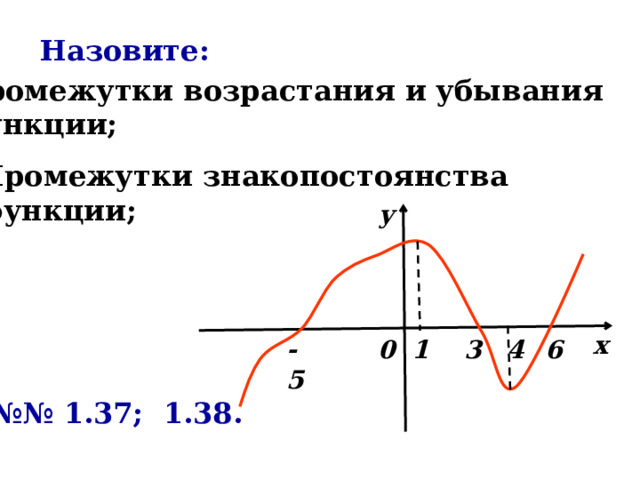
Назовите:

Промежутки возрастания и убывания

функции;

Промежутки знакопостоянства

функции;

y

x

4

6

3

1

-5

0

№№ 1.37; 1.38.

Изучение новых знаний

Число f(x 0 ) называют наибольшим значением функции f на множестве

M D(f), если существует такое число

x 0 M, что для всех x M выполняется неравенство

Изучение новых знаний

Число f(x 0 ) называют наименьшим значением функции f на множестве

M D(f), если существует такое число

x 0 M, что для всех x M выполняется неравенство

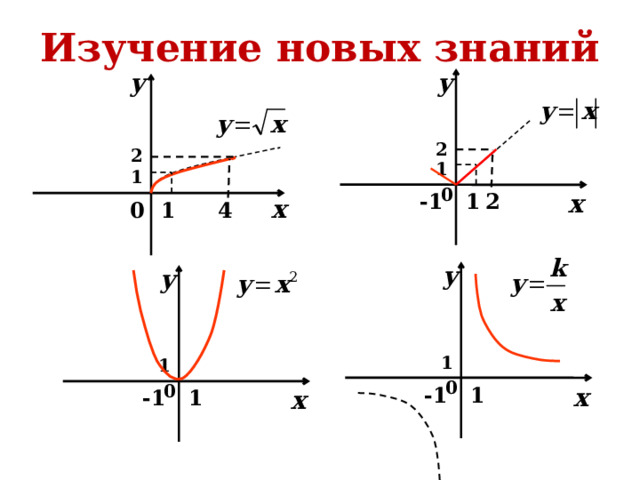
Изучение новых знаний

y

y

2

2

1

1

0

1

x

2

-1

x

0

1

4

y

y

1

1

0

0

-1

x

1

x

1

-1

Изучение новых знаний

y

Если f возрастает на [a;b], то

f(b)

f(a)

0

a

-1

x

b

y

Если f убывает на [a;b], то

f(a)

f(b)

0

-1

b

x

a

Изучение новых знаний

Функцию f называют четной, если для любого x из области определения функции выполняется равенство

Функцию f называют нечетной, если для любого x из области определения функции выполняется равенство

Изучение новых знаний

Выполнение одного из равенств

или означает, что область определения функции симметрична относительно начала координат, т.е. если то

Примеры:

Ось ординат является осью симметрии графика четной функции

Начало координат является центром симметрии графика нечетной функции

№№ 1.1; 1.3; 1.4; 1.5; 1.7; 1.8; 1.9.

Дома: №№ 1.2; 1.6; 1.10; 1.39; 1.47.