Свойства функций.
- Область определения функции.
- Область значений функции.
- Периодичность.
- Четность, нечетность.
- Наибольшее (наименьшее) значение функции.
- Нули функции.
- Промежутки знакопостоянства.
- Промежутки монотонности.
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёздв астрономии, между ориентирами в географии, контролировать системы навигации спутников.

Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

 Получите свидетельство
Получите свидетельство Вход
Вход





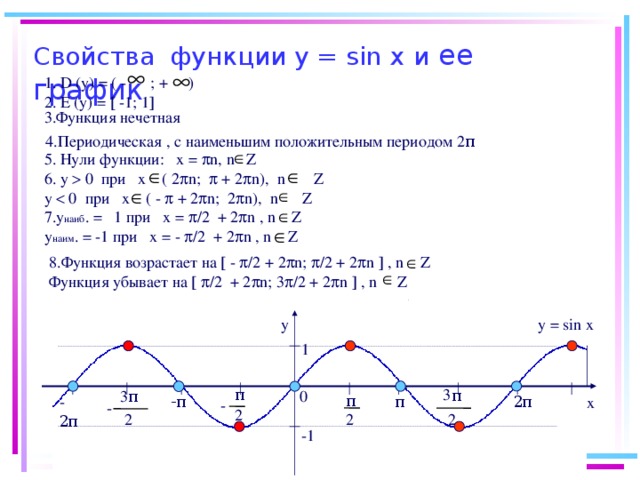
![Область определения Область значения функции у 1 D (у)=(- ; + ) х Е(у)= [ -1; 1 ] 2 π -1](https://fsd.videouroki.net/html/2015/09/12/98716012/img2.jpg)

 0 при 0 y 0 при х (2 π n; π +2 π n), n z y y 0 при х ( - π + 2 π n; 2 π n), n z " width="640"
0 при 0 y 0 при х (2 π n; π +2 π n), n z y y 0 при х ( - π + 2 π n; 2 π n), n z " width="640"

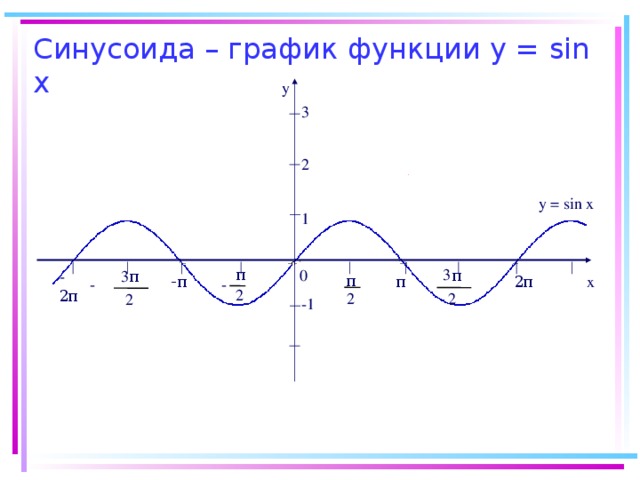
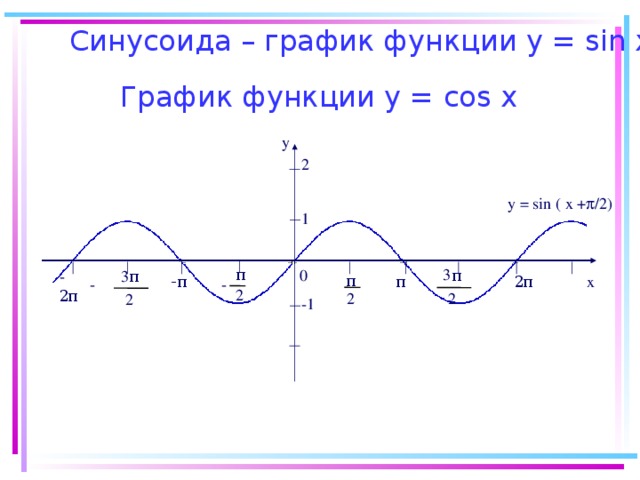










 Презентация к уроку алгебры на тему "Свойства и график функции y=sinx" (0.49 MB)
Презентация к уроку алгебры на тему "Свойства и график функции y=sinx" (0.49 MB)
 0
0 984
984 80
80 Нравится
0
Нравится
0


