"Мотивационный этап урока"

«Мотивационный этап урока»

Гедровец Ж. Н., учитель математики, МАОУ «Гимназия №16» г. Кунгура Пермского края

Мастерство управления деятельностью учащихся на уроках зависит от множества факторов. Педагогическое мастерство не всем дается от рождения. Его нужно развивать в себе, культивировать. Один учитель покоряет учеников, другой нагоняет скуку. На одних уроках ученики сидят, не шелохнувшись, а на других, дети постоянно отвлекаются, смотрят на часы, ждут конца урока.

В чем заключается педагогическое мастерство? Ясно одно: одним из важных компонентов педагогического мастерства является организация начала урока (начала изучения темы, раздела, предмета и т. д.).

Изучение психолого-педагогической литературы, освещающей передовой опыт учителей и современные образовательные технологии, позволили наметить некоторые требования к «вводному слову учителя»:

• Должна быть завязка урока (темы, раздела, курса…);

• Нужно задать определённую эмоциональную кривую, и базируясь на этой эмоциональной кривой, строить весь урок;

• Зная своё первое слово, нужно знать и последнее. Конец урока должен быть так же продуман, как и начало;

• Обязательно напомнить то, о чём был разговор раньше, сделать краткий обзор пройденного;

• Сразу поставить учащихся в известность о цели изучения той или иной темы;

• Использовать доступный язык, краткие, ясные фразы без витиеватых слова;

• Вовлекать учеников в процесс самостоятельного поиска и «открытия» новых знаний;

• Развивать познавательные интересы, любовь к математике;

• Решать вопросы проблемного характера, проводить исследовательскую работу;

• Использовать материал, показывающий практическую необходимость получения новых знаний;

• Знакомить учащихся с историческими аспектами развития вопросов;

• Учитывая возрастные особенности учащихся, использовать живые примеры, рассеивающие напряжённость;

• Использовать различные наглядные средства (таблицы, чертежи, модели и другое);

Рассмотрим некоторые примеры «вводных слов» на уроках математики.

Пример 1.

VII класс. Введение в предмет «алгебра».

С первого по седьмой класс вы изучали предмет – математику. «Есть о математике молва, что она в порядок ум приводит. Поэтому хорошие слова часто говорят о ней в народе». На уроках математики вы проводили вычисления с целыми и дробными числами, решали уравнения, задачи, знакомились с некоторыми фигурами и т. д. Всё это составляло содержание предмета «математика». Этот предмет подразделяют на самостоятельные дисциплины:

математика

алгебра

геометрия

Теория вероятностей

Математический анализ

Мы приступаем к изучению алгебры. Слово «алгебра» -арабского происхождения; великий учёный арабского мира Мухаммед ибн Мусса Аль-Хорезми жил и работал в IX веке нашей эры в Багдаде. Знаменитый труд великого учёного по праву считается первой книгой по алгебре (само слово «алгебра» восходит к арабскому «аль-джебр», одному из терминов книги Аль-Хорезми).

Это исследование посвящено решению уравнений. Родоначальник алгебраической науки не знал никакой символики и все свои выкладки описывал словами.

И только в XVI появились первые буквенные обозначения и математические знаки. Знаки «+» и

«-« впервые встречаются у немецких алгебраистов XVI веке. Решительный шаг в использовании символики был сделан французским математиком Франсуа Виет (1540-1603г.г.).

Современная алгебра –один из основных разделов математики. В школьной алгебре задачи решаются путём составления уравнений, изучают сами уравнения, связи между величинами. При этом используются буквы, выражения с буквами подвергаются различным преобразованиям. Но за всеми этими буквами чаще всего скрываются числа.

Иногда говорят: «Алгебра держится на четырёх китах: на уравнении, числе, тождестве, функции».

алгебра

функции

Уравнения, неравенства

число

Выражения и тождественные преобразования

Вы уже встречались в определённой мере с этими понятиями. При изучении алгебры мы углубим знания о числах, выражениях, уравнениях и расширим круг своих знаний в области математики. Итак, мы приступаем к изучению нового для вас предмета – «алгебра».

Пример 1.

VII класс. Как возникла геометрия.

Для первобытных людей важную роль играла форма окружавших их предметов. По форме и цвету, они отличали съедобные грибы от несъедобных, пригодные для построек породы деревьев от тех, которые годятся лишь на дрова и т. д. Добывая каменную соль, люди наталкивались на кристаллы, имевшие форму куба. Так, овладевая окружающим их миром, люди знакомились с простейшими геометрическими формами.

Различной была и геометрическая форма крестьянских полей. А для того, чтобы взимать налоги, надо было знать их площадь.

Гончару надо было знать, какую форму следует придать кубку или амфоре, чтобы в них входило то или иное количество жидкости. Астрономы, наблюдавшие за небом и дававшие на основе этих наблюдений указания, когда начинать полевые работы, должны были научиться определять положение звёзд на небе. Для этого понадобилось измерять углы. Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объёмы, и длины, и т. д.

Процесс знакомства с различными видами геометрических фигур сменился новым этапом-знакомством с их свойствами. И здесь главную роль играли практические задачи.

В жарком засушливом Египте успешно вести земледелие можно было только на полях, расположенных вблизи Нила. Весной, во время паводка, Нил широко разливался и покрывал поля своим плодородным илом. И лишь на удобренных этим илом полях могли получать египтяне урожаи ячменя, пшеницы и других возделываемых ими культур.

Так как население Египта было достаточно большим, то вся эта земля была поделена между крестьянами. Но вот в чём была неудача: поля отделялись друг от друга межами, а разлив Нила смывал каждую весну эти межи, и приходилось проводить их снова. Надо было знать, в каком направлении, и между какими точками следовало натягивать верёвки. А для этого был нужен план полей. Так из практической задачи о межевании полей возникла наука о землемерии. По-гречески земля называлась «геос», измеряю-«метрио», а поэтому и наука об измерении полей получила название «геометрия».

Современная геометрия значительно отличается от тех первых практических знаний, которыми пользовалось население Египта.

Впервые все знания в геометрических формах были собраны древнегреческим учёным Евклидом (III в. до н. э.), который представил эти знания в 13 книгах – «Начала».

Наша задача выяснить два существенных вопроса:

1. Что изучает предмет «геометрия»

2. Как изучают в геометрии эти формы?

Выводы: В данных примерах рассмотрено введение в предмет. В седьмом классе ребята начинают изучать новые для них предметы - алгебру и геометрию. На первых уроках учитель обязан ввести учащихся в этот предмет, дать исторические справки. Все исторические справки учитель сообщает ребятам в виде небольшого, хорошо продуманного, интересного рассказа. Рассказ может быть различной продолжительности, но он всегда должен занимать лишь небольшую часть урока.

Нередко рассказ учителя, раскрывая, историю вопроса или показывая его большую практическую значимость, служит основным источником пробуждения интереса учащихся к какой либо теме и стимулятором их активности в процессе изучения этой темы.

Пример 3.

VI класс. Изучение темы «Координатная плоскость».

Учитель начинает урок с чтения отрывка из книги «Соседи по планете» Ю. Дмитриева.

«Это произошло в 1942 году. Английскую подводную лодку атаковали фашистские самолёты и повредили её. Лодка вынужденно опустилась на дно. Гибель казалась неминуемой - из строя вышли рули и система всплытия. А вместе с людьми и боевым кораблём должно было погибнуть ценнейшее оборудование, впервые испытывавшееся на этой лодке. На борту корабля жили два голубя. Они стали последней, хотя и слабой надеждой моряков. К лапкам птиц прикрепили записки с указанием координат места нахождения лодки, поместили птиц в специальную капсулу и через торпедный аппарат выбросили капсулу наружу. И помощь пришла. Люди могли только догадываться, что пережили птицы, когда разыгрался жесточайший шторм. Голубь погиб, но голубка сумела долететь до базы. За этот подвиг она была удостоена высшей военной награды Великобритании, и ей был поставлен памятник».

Выделенный отрывок учитель читает детям без слов, которые подчеркнуты в тексте. Затем задаёт вопрос: «Что было написано в записке?». Ребята обычно хорошо воспринимают прочитанное, сильно переживая за моряков-подводников. Если удалось вызвать сопереживание, то появляется интерес. Тогда учащиеся легко находят ответ на заданный учителем вопрос. Учитель говорит, что сегодня на уроке будет рассмотрена тема «Координатная плоскость».

Пример 4.

VII класс. Изучение темы «Сумма углов треугольника».

Сегодня на уроке мы будем говорить о хорошо знакомой вам геометрической фигуре - о треугольнике. Вы знаете, что треугольник-это простейшая фигура: три стороны и три вершины -основные элементы треугольника. Математики его часто называют двумерным симплексом. «Симплекс» по-латыни означает простейший. Именно в силу своей простоты треугольник явился основой многих измерений. Эту фигуру изучали на протяжении многих веков многие учёные: Пифагор, Герон Александрийский, Леонард Эйлер и др. Треугольник любят инженеры за его удивительное свойство «жесткость» и «устойчивость»: даже если стержни, образующие треугольник, соединить шарнирно, то его невозможно изменить, в отличие от других многоугольников. Именно это обстоятельство заставляет инженеров при сооружении различных арок, перекрытий для крыш «разлагать» конструкции многоугольной формы на треугольники, внесением в них вспомогательных стержней-укосов. Вот почему очень важно знать такую фигуру, как треугольник и всё то, что с ним связано. Сегодня нам с вами предстоит решить очень важную задачу. Вам предлагается провести небольшое исследование: найти сумму углов треугольника.

Пример 5.

VI класс. Изучение темы «Длина окружности».

Одной из величин, изучаемых в школе, является длина. Мы изучали с вами тему «Длина отрезка». Что значит найти длину отрезка? Измерить отрезок, значит сравнить его с некоторым отрезком, принятым за единицу измерения. В результате мы получаем число, показывающее сколько раз единица измерения и ее часть укладывается в измеряемом отрезке. А как найти длину окружности? Длину окружности нельзя измерять прямолинейной мерой; криволинейная мера тоже сюда не подходит, так как на окружности укладывается только дуга самой окружности, для другой окружности эта дуга уже не годится. Ученики чертят окружности с различными диаметрами, и сами могут прийти к выводу, что длина окружности явно зависит от величины диаметра. Стало быть окружность нужно измерять ее собственным диаметром, другими словами -нужно узнать, сколько раз диаметр содержится в собственной окружности. Далее с учащимися организуется лабораторная работа для нахождения длины окружности.

Выводы: в примерах 3-5 учитель начал уроки с постановки математической проблемы. Существенным условием проблемного обучения является исследовательский характер работы учащихся в процессе обучения. Сейчас уже общепризнано, что урок в школе не считается эффективным, если на этом уроке учащиеся не работают активно и самостоятельно, не решают задач, требующих не только определённых знаний, но и определённой сообразительности, догадки. Следует заметить, что проблемное обучение включает в себя не только постановку вводной задачи, создания проблемной ситуации, но и самостоятельную творческую работу учащихся над данной ситуацией, открытие им новых свойств, обоснование всех своих рассуждений.

Пример 6.

V класс. Вводится понятие точного и приближённого числа.

Числа окружают нас всюду. Ещё Пифагор говорил: «Всё есть число». У Николая Гумилёва есть замечательные слова: «…Все оттенки смысла умное число передаёт». Мы так к ним привыкли, что порой не отдаём себе отчёта в том, что же такое число? Язык чисел служит универсальным языком для описания закономерностей окружающего мира. Мне бы хотелось прочитать вам небольшую статью о нашем городе Кунгуре.

«В отличие от многих своих собратьев – малых российских городов, не оставивших заметного следа в истории, старинный Кунгур именит и родовит. По указу царя Алексея Михайловича Романова у слияния трёх рек – Сылвы, Ирени и Шаквы в 1663 году был заложен город Кунгур. Город быстро рос и богател. Славен наш город историей. В 1774 году жители отважно отбились от пугачёвских войск. Из-за своей патриархальности Кунгур многие годы служил местом съёмок для фильмов, было отснято четыре фильма: «Тени исчезают в полдень», «Приваловские миллионы», «Один и без оружия», «Покушение на Гоуэро». В 2008 году праздновал свой юбилей-345 лет. Город Кунгур занимает площадь 56 кв. км. В настоящее время в нём проживает 70000 человек». Данная статья содержит не всю информацию о городе, но кое-что нового и интересного для себя вы узнали. Обратили ли вы на то, что в статье присутствуют числа. Можно ли сказать, что все эти числа являются точными? Время образования города, площадь, численность населения и т. д. Конечно же, нет. На данном примере можно сказать, что не все значения бывают точными. В реальности существуют кроме точных значений, ещё и приближённые значения. Точные значения обычно придаются величинам, которые можно характеризовать, пользуясь только натуральными числами (например, число учеников в классе, рек, школ и т. д.). приближенные значения обычно придаются величинам, которые нужно измерять (расстояние, время, площадь, объём, температура), или же которые получаются в результате счёта большого числа предметов. А объясняется это тем, что при изготовлении измерительных приборов не может быть достигнута их идеальная точность (на приборах указывается их погрешность), да и сам человек, пользующийся измерительными приборами, допускает погрешность. Итак, предметом нашего разговора сегодня будут приближённые числа.

Пример 7.

VI класс. Отрицательные числа.

Учитель начина урок с задачи: «Катер отошёл от пристани на а км вниз по реке, затем развернулся и отошёл в км вверх по реке. Где находится сейчас катер?» Учитель разбирает решение задачи вместе с учащимися. Решение этой задачи приводит к вычислению разности х=а-в, выражающей расстояние катера от пристани в определённом направлении. Дальше можно предложить ребятам подставить конкретные значения а и в. Если, например, а=50 и в=40, то получаем х=10 и ответ на вопрос задачи: катер находится на расстоянии 10 км от пристани вниз по реке. Если а=50 и в=50, то получаем х=0 и ответ на вопрос задачи: катер находится у пристани. Если же а=40 и в=50, то решение задачи по формуле 1 приводит к вычитанию из меньшего числа большего, что невозможно в множестве 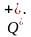Здесь то и обнаруживается недостаточность этого множества, а вместе с этим и необходимость его расширения таким образом, чтобы задача была разрешена по формуле 1 в любых случаях. Эти соображения приводят нас к расширению множества 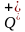, т. е. введение отрицательных чисел.

В примерах 6-7 рассмотрены введения новых понятий. Здесь учитель использует межпредметные связи (история родного города), рассматривает сначала примеры, а потом вводит новые понятия. Рассмотрев примеры, ученики сами участвуют в составлении определений. Когда ученик участвует в составлении определения, он действительно слушает и больше понимает. Материал глубже усваивается, активизируется способность к познанию нового, развивается мышление. Это способствует экономии времени при изучении последующего материала и повышает уровень усвоения.