МНОГОГРАННИК - геометрическое тело

МНОГОГРАННИКИ

Презентация

преподавателя математики

Чановой Н.А.

ЕТ «Автоматика»

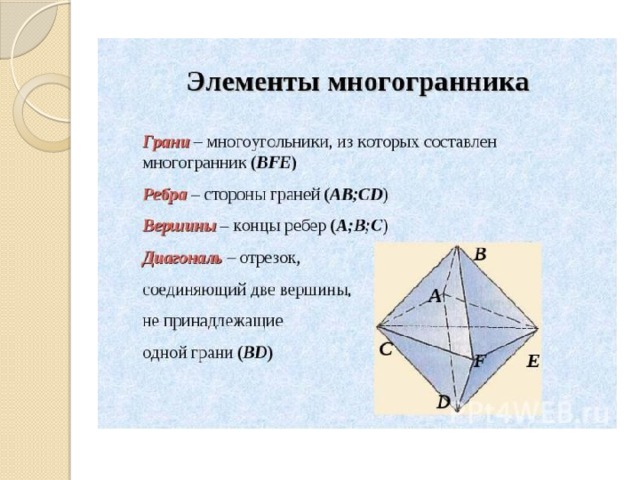
Определение

• Многогранник , точнее  трёхмерный многогранник  — совокупность конечного числа плоских  многоугольников  в трёхмерном  евклидовом пространстве .

• МНОГОГРА́ННИК  -геометрическое тело, ограниченное со  всех сторон плоскими многоугольниками. 

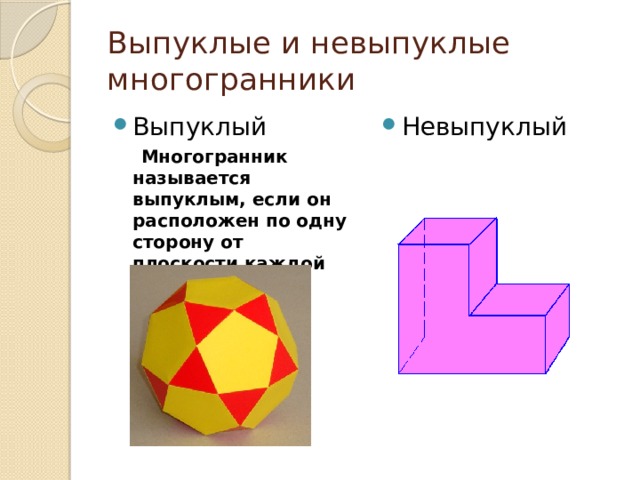
Выпуклые и невыпуклые многогранники

• Выпуклый

• Невыпуклый

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

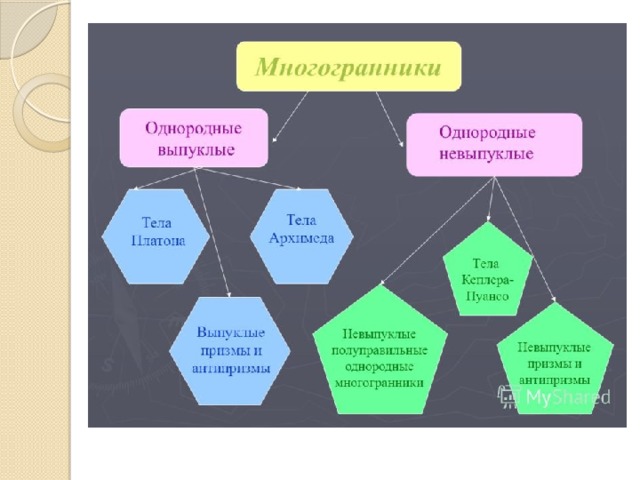
Многогранники

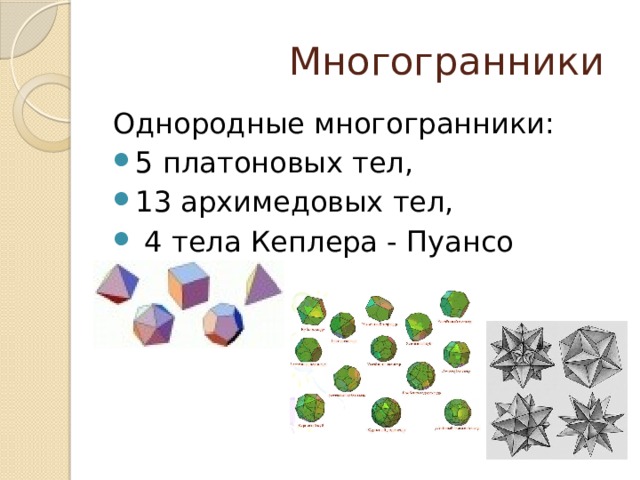
Однородные многогранники:

• 5 платоновых тел,
• 13 архимедовых тел,
• 4 тела Кеплера - Пуансо

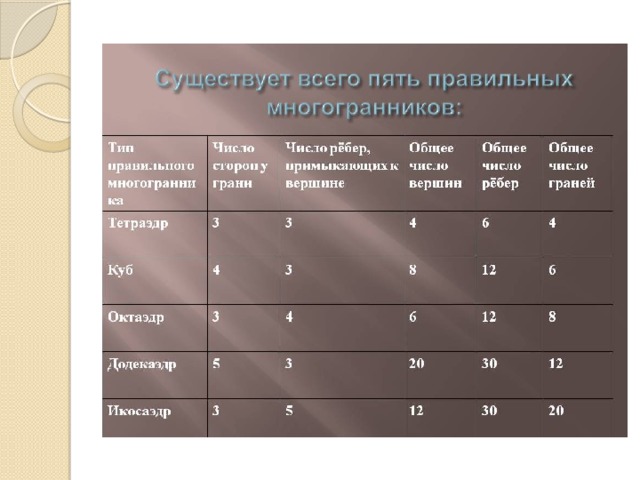
Правильные многогранники

• Правильный многогранник  или  плато́ново тело  — это  выпуклый многогранник , состоящий из одинаковых  правильных многоугольников  и обладающий пространственной симметрией.

Платоновы тела

Архимед

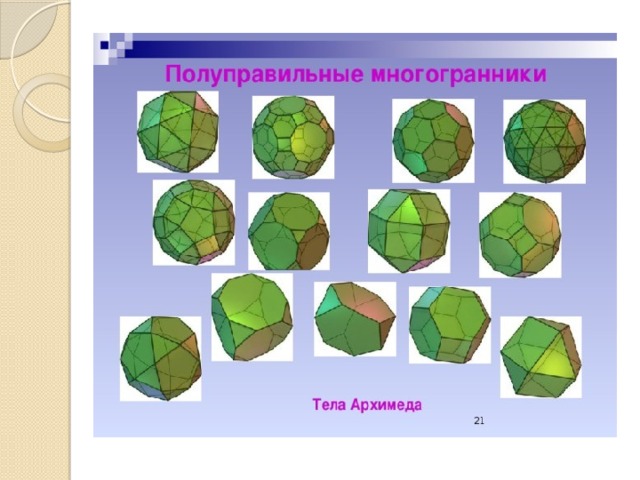
• Известно еще множество совершенных тел, получивших название полуправильных многогранников или Архимедовых тел. У них также все многогранные углы равны и все грани – правильные многоугольники, но несколько разных типов. Существует 13 полуправильных многогранников, открытие которых приписывается Архимеду.

Иоган Кеплер и Луи Пуансо

• Всего 4! В 1811 году Коши установил, что существуют всего 4 правильных звёздчатых тела, которые не являются соединениями платоновых и звёздчатых тел. К ним относятся открытые в 1619 году Иоганном Кеплером малый звёздчатый додекаэдр и большой звёздчатый додекаэдр, а также большой додекаэдр и большой икосаэдр, открытые в 1809 году Луи Пуансо. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кеплера — Пуансо.

Тела Кеплера - Пуансо

• Малый звёздчатый додекаэдр
• Большой додекаэдр
• Большой звёздчатый додекаэдр
• Большой икосаэдр

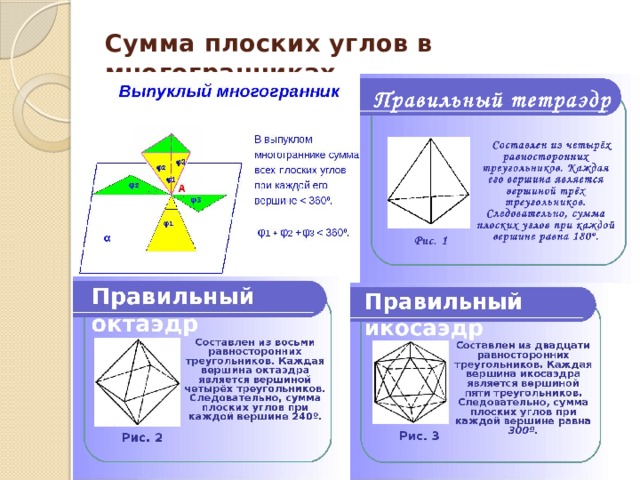
Сумма плоских углов в многогранниках

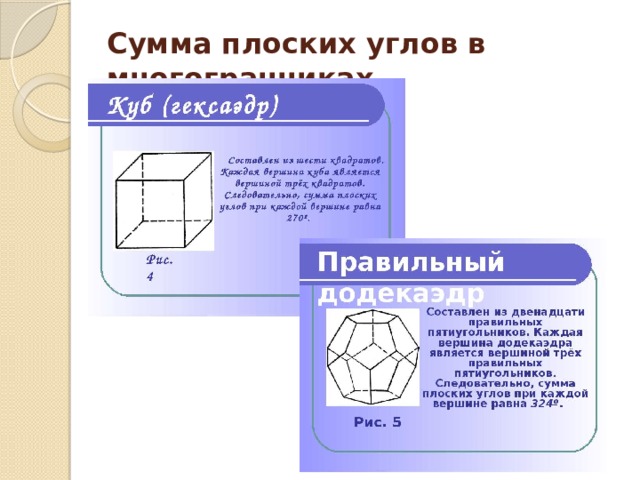
Сумма плоских углов в многогранниках

Многогранники в природе

Многогранники в архитектуре

Многогранники в жизни

Спасибо

за внимание