Цели:
систематизировать знания об основных видах многогранников, показать их применение в других видах деятельности,
формировать и развивать эвристическое мышление, показать, какую роль играет математика в развитии общества, развивать самостоятельность, творчество, морально-эстетические качества личности.
Форма проведения: групповая (ученики заранее делятся на три группы: «историки», «математики» и «биологи»). Все три группы пишут рефераты по данным темам: «историки» связывают раздел «Многогранники» с историей математики; «математики» исследуют тему с математической точки зрения; «биологи» ищут связи многогранников с биологией, а также роль и место многогранников в природе; изучая рефераты, учитель предлагает, что лучше всего стоит продемонстрировать на конференции.
Ход урока.
Учитель. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. «Правильных многогранников вызывающе мало, — написал когда-то Л. Кэрролл, — но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» (ГЦ}.
Сегодня на уроке мы поговорим о многогранниках, а точнее о том, где встречаются многогранники в природе. А также услышим мнения ученых древности об использовании многогранников.
Учитель. Как много существует правильных многогранников?
«Математики». Существует всего пять таких многогранников.
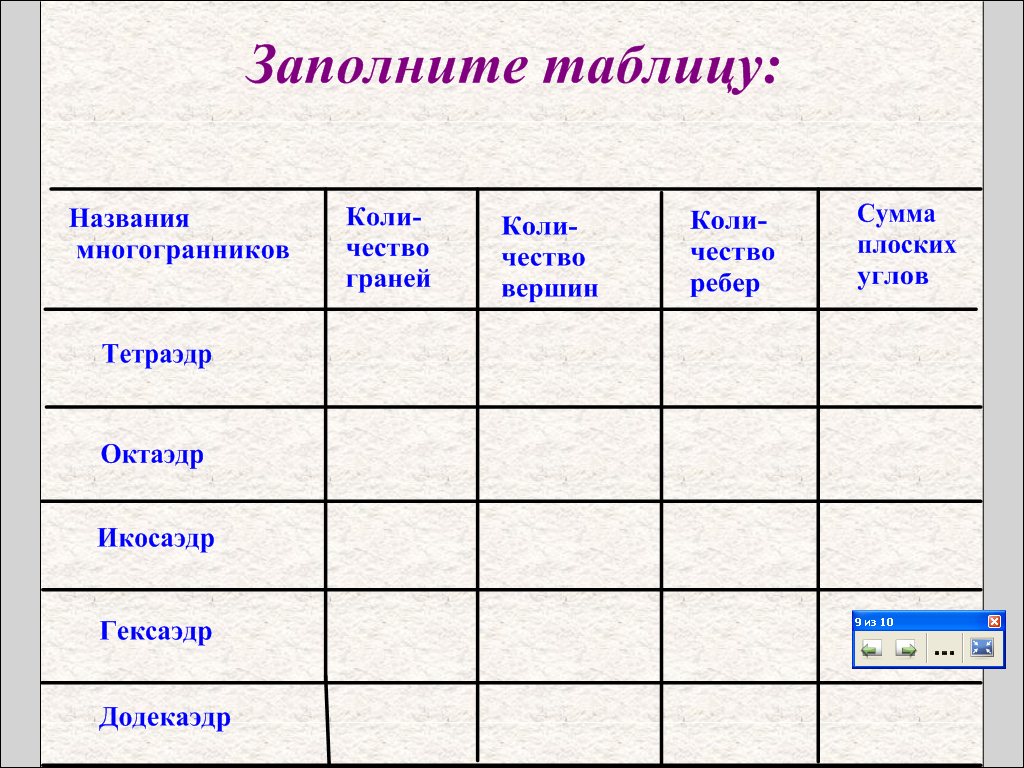
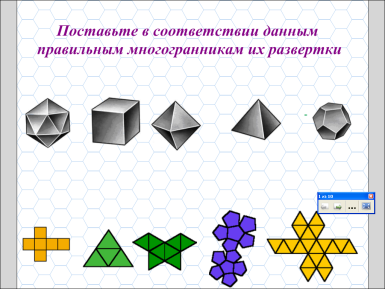
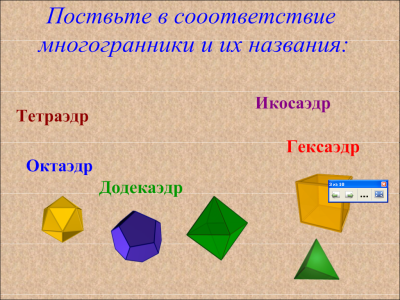
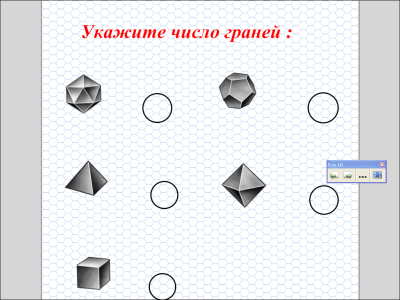
И далее доказывают, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, га-угольники при га > 6. После доказательства показывают модели правильных многогранников (тетраэдр, додекаэдр, икосаэдр, октаэдр). Говоря, например, о додекаэдре, уточняют, что додекаэдр составлен из двенадцати правильных пятиугольников, каждая его вершина является вершиной трех пятиугольников, а сумма плоских углов при каждой вершине равна 324°; таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
«Историки». Интерес к многогранникам человек проявляет на протяжении всей своей сознательной жизни — и малым ребенком, играющим деревянными кубиками, и зрелым математиком.
Пчелы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел (подобных пирамидам) уходит вглубь веков. Пять правильных тел изучали Театет, Платон, Евклид, Гипсикл, Папп. Платон связал с этими телами формы атомов основных стихий природы. (Стихиями натурфилософы называли вещества, из которых путем сгущения и разряжения, охлаждения и нагревания образуются все тела.)
Пифагорейцы считали, что огонь состоит из мельчайших (а потому невидимых) частиц, имеющих форму тетраэдра. Их воззрения основывались на том, что поскольку среди выпуклых правильных тел тетраэдр обладает наименьшим числом граней и наиболее «острыми» многогранными углами при вершинах, то он обладает наибольшей проникающей способностью.

Правильный тетраэдр представляет собой простейшее из пяти Платоновых тел. Он настолько прост, что был известен еще древним египтянам, а математики изучали геометрические свойства тетраэдра одновременно с изучением свойств куба. Тетраэдр обладает рациональной конструкцией: высокой прочностью при малом весе. Наиболее неподвижной из стихий — земле — пифагорейцы ставили в соответствие самый устойчивый многогранник — куб.
И. Кеплер (1571-1630) написал этюд «О снежинке», в котором высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных — куб, а его, если позволительно так сказать, супруга — октаэдр, ибо у октаэдра столько углов, сколько у куба граней».
«Историки». С помощью простых и сложных атомов Платон попытался даже отразить взаимоотношения между стихиями:
1 вода = 2 воздух + 1 огонь.
Это «уравнение» надо понимать так: в элементе воды — икосаэдре — 20 граней, образованных равносторонними треугольниками, которые, в свою очередь, составлены шестью прямоугольными треугольниками. Платон представлял атомы как плоские тела — прямоугольные «треугольники двух видов: одни равнобедренные, другие с катетом, равным половине гипотенузы. Следовательно, сложный атом икосаэдр состоит из 6 * 20 = 120 простых атомов-треугольников. В элементе воздуха восемь граней, а значит, 6 * 8 = 48 треугольников. Но по уравнению взято два элемента воздуха, поэтому общее число треугольников 48 * 2 = 96. В элементе огня четыре грани, а значит, 6 * 4 = 24 треугольника. Итак, равенство соблюдено — 20 граней и 120 треугольников:
(8-2 + 4) граней и (48 * 2 + 24) треугольников
«Биологи».
Математики говорили, что пчелы строили свои шестиугольные соты задолго до появления человека. Мы сейчас попытаемся пояснить, почему пчелы строят соты именно так.
Пчелы — удивительные создания. Если разрезать пчелиные соты плоскостью, то станет видна сеть равных друг другу правильных шестиугольников. Из правильных многоугольников с одинаковой площадью наименьший периметр именно у правильных шестиугольников.
Стало быть, мудрые пчелы экономят воск и время для постройки сот. На рисунке 4 изображена пчелиная ячейка в общем виде, а на рисунке 5 можно увидеть, как соприкасаются ячейки в улье: их общая часть является ромбом. Какая же здесь выгода для пчел? А дело вот в чем.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход





 Это «уравнение» надо понимать так: в элементе воды — икосаэдре — 20 граней, образованных равносторонними треугольниками, которые, в свою очередь, составлены шестью прямоугольными треугольниками. Платон представлял атомы как плоские тела — прямоугольные «треугольники двух видов: одни равнобедренные, другие с катетом, равным половине гипотенузы. Следовательно, сложный атом икосаэдр состоит из 6 ■ 20 = 120 простых атомов-треугольников. В элементе воздуха восемь граней, а значит, 6 • 8 = 48 треугольников. Но по уравнению взято два элемента воздуха, поэтому общее число треугольников 48 • 2 = 96. В элементе огня четыре грани, а значит, 6 • 4 = 24 треугольника. Итак, равенство соблюдено — 20 граней и 120 треугольников:
Это «уравнение» надо понимать так: в элементе воды — икосаэдре — 20 граней, образованных равносторонними треугольниками, которые, в свою очередь, составлены шестью прямоугольными треугольниками. Платон представлял атомы как плоские тела — прямоугольные «треугольники двух видов: одни равнобедренные, другие с катетом, равным половине гипотенузы. Следовательно, сложный атом икосаэдр состоит из 6 ■ 20 = 120 простых атомов-треугольников. В элементе воздуха восемь граней, а значит, 6 • 8 = 48 треугольников. Но по уравнению взято два элемента воздуха, поэтому общее число треугольников 48 • 2 = 96. В элементе огня четыре грани, а значит, 6 • 4 = 24 треугольника. Итак, равенство соблюдено — 20 граней и 120 треугольников:









 Разработка урока по геометрии "Многогранники вокруг нас" (1.55 MB)
Разработка урока по геометрии "Многогранники вокруг нас" (1.55 MB)
 0
0 571
571 58
58 Нравится
0
Нравится
0



