Многогранники 2 курс

||

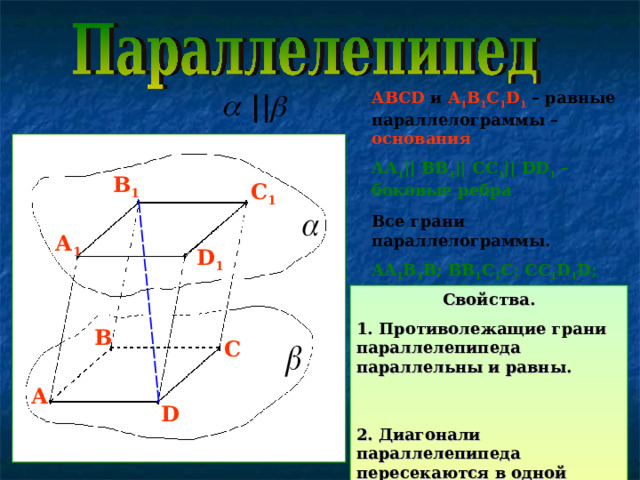
АВС D и A 1 B 1 C 1 D 1 – равные параллелограммы – основания

АА 1 || ВВ 1 || СС 1 || DD 1 – боковые ребра

Все грани параллелограммы.

AA 1 B 1 B; BB 1 C 1 C; CC 1 D 1 D; AA 1 D 1 D – боковые грани

DB 1 – диагональ

В 1

С 1

А 1

D 1

Свойства.

1. Противолежащие грани параллелепипеда параллельны и равны.

2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

В

С

А

D

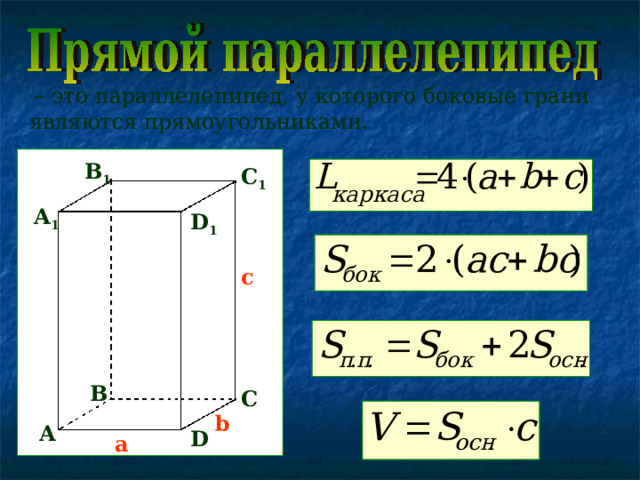
– это параллелепипед, у которого боковые грани являются прямоугольниками.

B 1

С 1

A 1

D 1

c

В

С

b

А

D

a

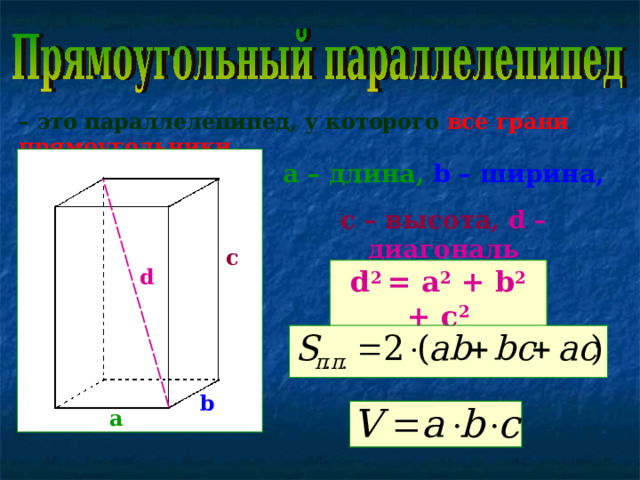
– это параллелепипед, у которого все грани прямоугольники .

a – длина, b – ширина,

с – высота , d – диагональ

c

d

d 2 = a 2 + b 2 + c 2

b

а

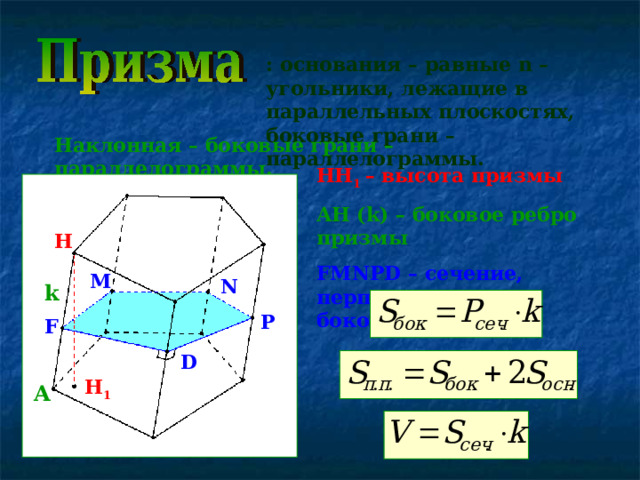
: основания – равные n – угольники, лежащие в параллельных плоскостях, боковые грани – параллелограммы.

Наклонная – боковые грани – параллелограммы.

HH 1 – высота призмы

AH ( k ) – боковое ребро призмы

FMNPD – сечение, перпендикулярное боковому ребру

H

M

N

k

P

F

D

H 1

A

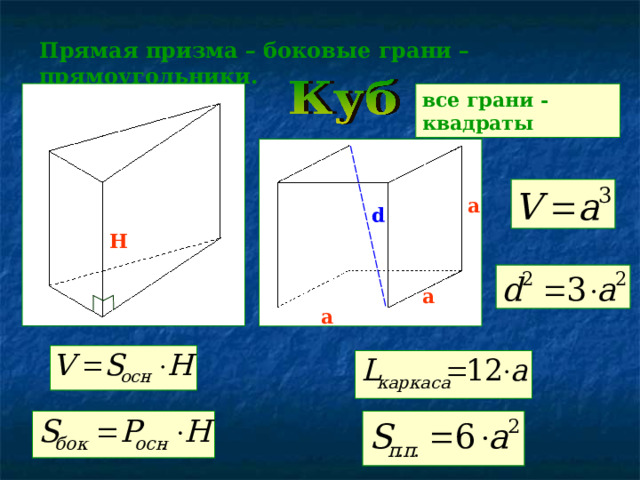
Прямая призма – боковые грани – прямоугольники.

все грани - квадраты

а

d

H

а

а

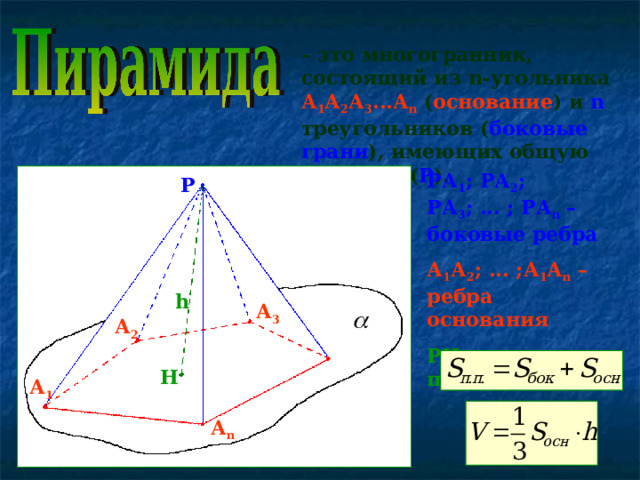
– это многогранник, состоящий из n -угольника А 1 А 2 А 3 ...А n ( основание ) и n треугольников ( боковые грани ), имеющих общую вершину ( Р ).

РА 1 ; РА 2 ; РА 3 ; ... ; РА n – боковые ребра

А 1 А 2 ; ... ;А 1 А n – ребра основания

Р H – высота пирамиды - h

Р

h

А 3

А 2

H

А 1

А n

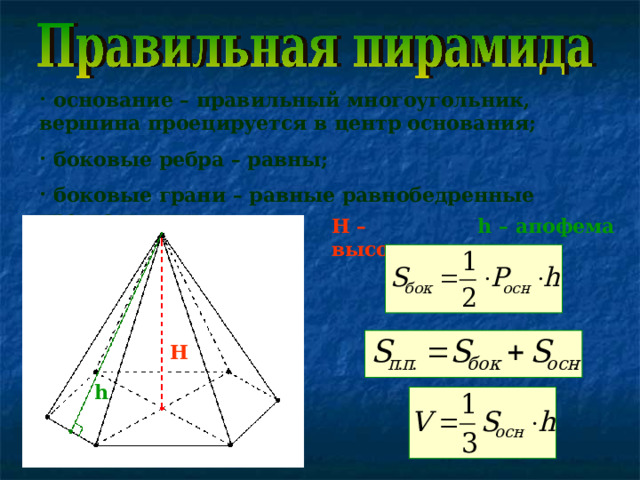
• основание – правильный многоугольник, вершина проецируется в центр основания;
• боковые ребра – равны;
• боковые грани – равные равнобедренные треугольники.

H – высота,

h – апофема

H

h

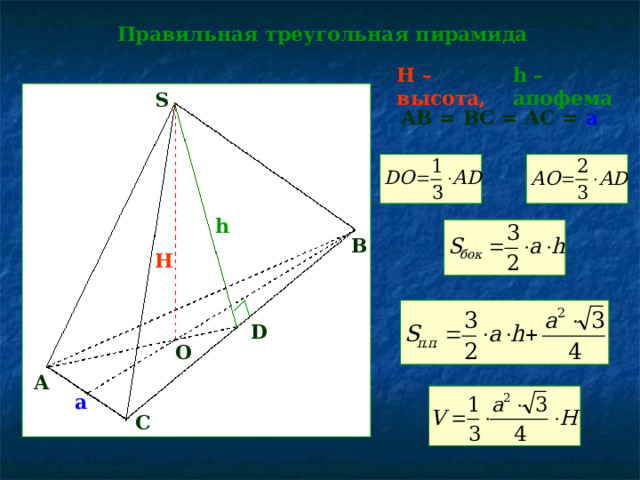
Правильная треугольная пирамида

h – апофема

H – высота,

S

AB = BC = AC = a

h

B

H

D

O

A

a

C

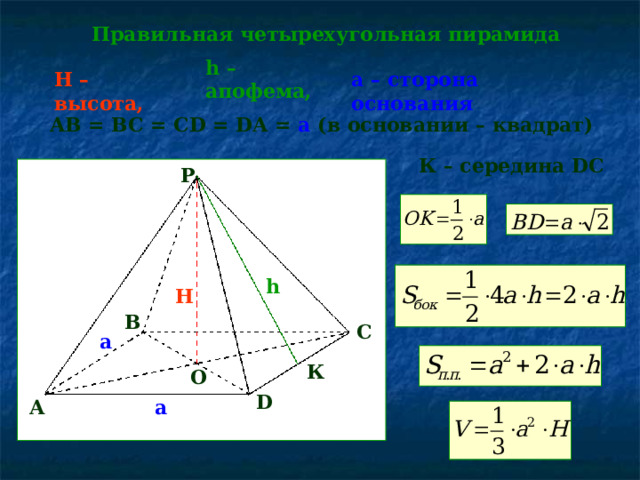
Правильная четырехугольная пирамида

h – апофема,

а – сторона основания

H – высота,

AB = BC = CD = DA = a ( в основании – квадрат)

К – середина DC

P

h

H

B

C

a

К

O

D

A

a

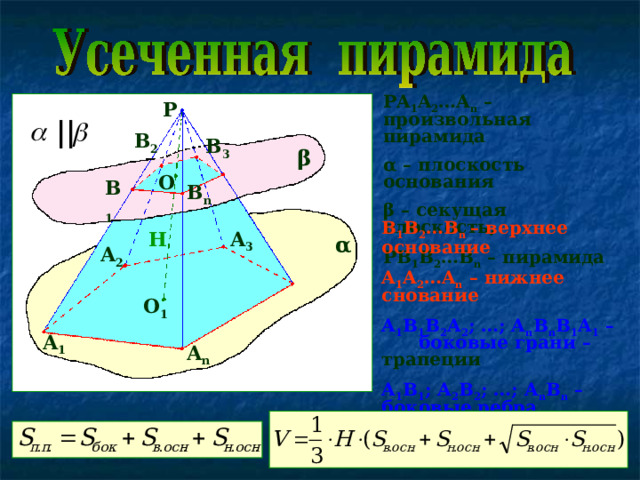
PA 1 A 2 …A n – произвольная пирамида

α – плоскость основания

β – секущая плоскость,

PB 1 B 2 …B n – пирамида

P

||

B 2

B 3

β

O

B 1

B n

B 1 B 2 …B n – верхнее основание

A 1 A 2 …A n – нижнее снование

A 1 B 1 B 2 A 2 ; …; A n B n B 1 A 1 – боковые грани – трапеции

A 1 B 1 ; A 2 B 2 ; …; A n B n – боковые ребра

OO 1 = H – высота

A 3

H

α

A 2

O 1

A 1

A n

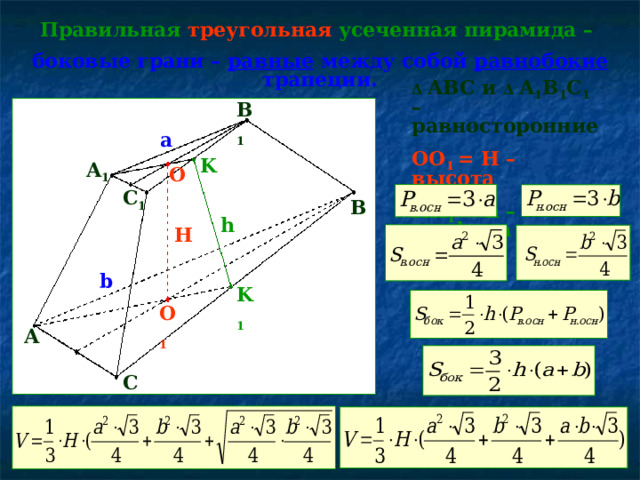
Правильная треугольная усеченная пирамида –

боковые грани – равные между собой равнобокие трапеции.

Δ ABC и Δ A 1 B 1 C 1 – равносторонние

OO 1 = H – высота

КК 1 = h – апофема

B 1

a

K

A 1

O

C 1

B

h

H

b

K 1

O 1

A

C

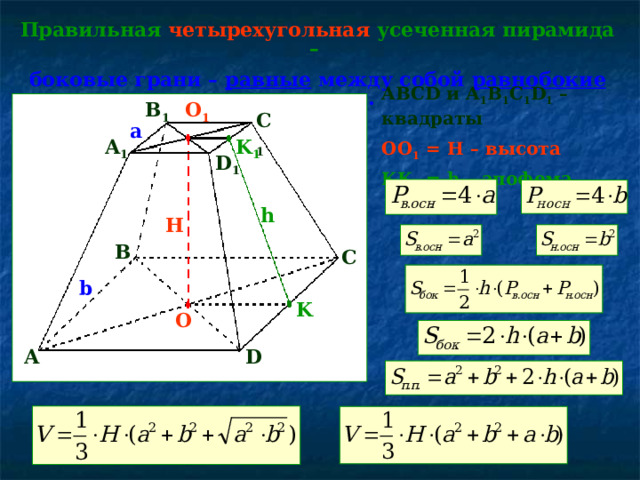
Правильная четырехугольная усеченная пирамида –

боковые грани – равные между собой равнобокие трапеции.

ABCD и A 1 B 1 C 1 D 1 – квадраты

OO 1 = H – высота

KK 1 = h – апофема

B 1

O 1

C 1

a

K 1

A 1

D 1

h

H

B

C

b

K

O

A

D