Элективный курс по матемтаике "Многогранники"

I. Вводная часть. Введение

В последнее десятилетие одним из наиболее популярных в практике школьного обучения стал метод проектов, который изначально понимался как организация специальной исследовательской деятельности учащихся в какой - либо практической области. На сегодняшний день в нашей стране не так много информации об использовании метода проектов в обучении математике. Очевидно, сложность самой математики часто служит оправданием для традиционной позиции учителя, ведь проще подробно объяснить и «нарешать» определенное количество стандартных примеров, чем создать детям условия для самостоятельного изучения нового.

Опираясь на свой многолетний опыт работы в школе, я заметила, что большинство учащихся не слишком увлекает геометрия. Они не склонны считать этот предмет особо притягательным. Решение геометрических задач требует от учащихся хорошо развитого абстрактного представления и логического мышления, исследовательских навыков, графической культуры.

Изучение элективного курса «Многогранники» дает возможность вызвать у учащихся интерес к изучению геометрии, способствует познанию ее серьезного прикладного значения, формирует целостную картину мира. «Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности - от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книги Бранко Грюнбаума «Выпуклые многогранники». Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие - в виде вирусов. Пчелы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел наряду с другими видами пластических искусств уходит в глубь веков».

Исходя из такого взгляда на данную проблему, я считаю содержание предложенного курса актуальным.

Цель: при реализации курса «Многогранники» с помощью исследовательской, поисковой и практической деятельности познакомить учащихся с правильными, полуправильными, звездчатыми многогранниками и их значением в современном мире; подготовить к решению практических задач (научить строить, конструировать многогранник и описывать его свойства).

Курс «Многогранники» ориентирован на удовлетворение индивидуальных учебных и будущих профессиональных потребностей.

Задачи:

 - формирование у обучающихся навыков исследовательской деятельности, умений анализировать, рассуждать и на основании этого делать выводы;

 - развитие сообразительности и наблюдательности, творческих способностей, интереса к геометрии и формирование умения решать практические задачи;

 - включение учащихся в поисковую деятельность как фактор личностного развития;

 - развитие коммуникативных навыков, умения участвовать в дискуссии;

 - воспитание у обучающихся эстетического вкуса;

 - развитие целостного, научно обоснованного с геометрической точки зрения, представления о современном мире.

Включенный в программу материал может применяться для разных групп школьников за счет интересного содержания.

Планирование курса:

Весь материал - смотрите документ.

Программа элективного курса

« Многогранники»

Выполнила: Сафронова Людмила Владимировна,

учитель математики

ГБОУ СОШ с. Хворостянка

м.р. Хворостянский

Самарской области

2014г.

Оглавление

I. Вводная часть

Актуальность……………………………………………3 стр.

Цели и задачи…………………………………………....4 стр.

Ожидаемые результаты…………………………………4 стр.

II. Основная часть

Теоретический блок……………………………………..5 стр.

Содержательно-технологический блок ……………….7 стр.

Контрольно-оценочный блок………………………….10 стр.

Ресурсный блок (условия)……………………………..11 стр.

III. Заключение

Выводы…………………………………………………..11 стр.

Прогноз: эффекты и риски……………………………. 12 стр.

IV. Информационные источники……………………………………… 12 стр.

I. Вводная часть. Введение

В последнее десятилетие одним из наиболее популярных в практике школьного обучения стал метод проектов, который изначально понимался как организация специальной исследовательской деятельности учащихся в какой-либо практической области. На сегодняшний день в нашей стране не так много информации об использовании метода проектов в обучении математике. Очевидно, сложность самой математики часто служит оправданием для традиционной позиции учителя, ведь проще подробно объяснить и «нарешать» определенное количество стандартных примеров, чем создать детям условия для самостоятельного изучения нового.

Опираясь на свой многолетний опыт работы в школе, я заметила, что большинство учащихся не слишком увлекает геометрия. Они не склонны считать этот предмет особо притягательным. Решение геометрических задач требует от учащихся хорошо развитого абстрактного представления и логического мышления, исследовательских навыков, графической культуры.

Изучение элективного курса «Многогранники» дает возможность вызвать у учащихся интерес к изучению геометрии, способствует познанию ее серьезного прикладного значения, формирует целостную картину мира. «Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности - от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книги Бранко Грюнбаума «Выпуклые многогранники». Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие - в виде вирусов. Пчелы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел наряду с другими видами пластических искусств уходит в глубь веков».

Исходя из такого взгляда на данную проблему, я считаю содержание предложенного курса актуальным.

Цель: при реализации курса «Многогранники» с помощью исследовательской, поисковой и практической деятельности познакомить учащихся с правильными, полуправильными, звездчатыми многогранниками и их значением в современном мире; подготовить к решению практических задач (научить строить, конструировать многогранник и описывать его свойства).

Курс «Многогранники» ориентирован на удовлетворение индивидуальных учебных и будущих профессиональных потребностей.

Задачи:

- формирование у обучающихся навыков исследовательской деятельности, умений анализировать, рассуждать и на основании этого делать выводы;

- развитие сообразительности и наблюдательности, творческих способностей, интереса к геометрии и формирование умения решать практические задачи;

- включение учащихся в поисковую деятельность как фактор личностного развития;

- развитие коммуникативных навыков, умения участвовать в дискуссии;

- воспитание у обучающихся эстетического вкуса;

- развитие целостного, научно обоснованного с геометрической точки зрения, представления о современном мире.

Включенный в программу материал может применяться для разных групп школьников за счет интересного содержания.

ОЖИДАЕМЫЕ РЕЗУЛЬТАТЫ ОБУЧЕНИЯ

По окончанию изучения курса учащиеся должны уметь:

- определять вид многогранника, знать его свойства, находить примеры его применения в окружающем мире;

- понимать прикладной характер геометрических законов;

- видеть основополагающее значение многогранников в физике, химии т.д.;

- находить нужную информацию из различных источников, пользоваться Интернет-ресурсами;

- научиться решать прикладные задачи на многогранники.

II. Основная часть

1. Теоретический блок

Данный элективный курс рассчитан в первую очередь на учащихся 10-11 классов, желающих расширить и углубить свои знания по математике, сделать правильный выбор будущей профессии.

Материал этого курса привлечет внимание тех учащихся, которым интересна геометрия, ее приложения к различным отраслям знаний.

Основные приоритеты:

-обучение через самостоятельную исследовательскую работу;

-междисциплинарная интеграция (связь с черчением, химией, физикой, биологией, географией, астрономией, изобразительным искусством);

-учет будущих профессиональных потребностей.

Методологическими основаниями при разработке данного курса являлись: субъектный подход, принципы научности, системности, активности, целесообразности.

Данный элективный курс поможет учителю в выработке у учащихся навыков исследовательского труда и привитии интереса к геометрии.

Курс «Многогранники» предусматривает следующее:

- работа с учебной и справочной литературой;

- практикум по изготовлению фигур многогранников;

- использование ресурсов Интернета;

- создание презентаций;

- устные сообщения учащихся о результатах исследований;

- лабораторная работа с микроскопом по изучению формы кристаллов;

- экскурсии, дискуссии;

- проектная и исследовательская работа;

- индивидуальные консультации с учителем;

-практикум по решению прикладных задач с использованием инженерной графики.

С целью определения динамики интереса необходимо:

- создание индивидуальной образовательной траектории усвоения материала курса;

- исследовательская работа должна быть направлена на получение конечного продукта;

- собеседование в процессе труда;

- содержание теоретического материала должно вызвать стремление к познанию окружающего мира.

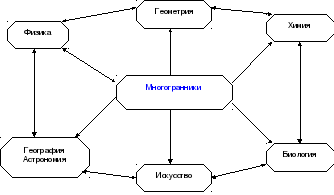
Перед организацией работы учащихся нужно провести вводное анкетирование, чтобы выяснить профессиональные интересы и уровень имеющихся знаний по данному вопросу. Затем распределить всех в группы по интересам: геометры, биологи, физики, химики, географы, астрономы, искусствоведы и т.д.

Ведущую роль в организации и проведении тематических занятий будет иметь не только преподаватель, но и члены создаваемых групп по интересам. Этот элективный курс отличается тем, что он охватывает широкий круг различных предметов, дает возможность увидеть основополагающую роль многогранников в существующем мироздании. Каждая группа имеет свое задание в общей цели. (Приложение №1. Анкета)

РЕЗУЛЬТАТЫ АНКЕТИРОВАНИЯ

Увлечены и интересуются:

ПРИМЕРНЫЕ ТЕМЫ ПРОЕКТОВ И ТВОРЧЕСКИХ РАБОТ:

1. Исследовательский проект (лабораторный эксперимент) по выращиванию кристаллов соли «Многогранник и химия».

2. Практико-ориентированный проект (работа практической лаборатории) «Модели многогранников».

3. Игровой проект (деловая игра) «Путешествие многогранника по страницам географии и астрономии».

4. Информационный проект «Многогранник и искусство».

5. Редакционно-издательский проект (выпуск сборника задач «Многогранник и его свойства в решении практических задач», сборник сочинений и стихов «Нас многогранник вдохновил»).

2. Содержательно-технологический блок

Важнейшими составляющими математического образования являются «математический язык, связь с другими науками и практикой, специфика творческой математической деятельности, история математики». Исходя из этих параметров, выстроена структура предлагаемого элективного курса «Многогранники».

1. Тема 1. Выпуклые многогранники

   • Определение многогранника.

   • Теорема Коши.

   • Икосаэдральная игра Гамильтона, открытие в 1960 ромбододекаэдра ученым Билински.

2. Тема 2 . Теорема Эйлера

3. Тема 3. Правильные многогранники:

• тетраэдр;

• гексаэдр;

• октаэдр;

• додекаэдр;

• икосаэдр.

1. Тема 4. Полуправильные многогранники

• Архимедовы тела, полученные усечением: усеченные (тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр).

• Квазиправильные многогранники (кубооктаэдр, икосододекаэдр).

• Ромбокубооктаэдр, ромбоикосододекаэдр.

• «Курносые» модификации куба, додекаэдра.

1. Тема 5. Звездчатые многогранники

• Пентаграмма (символ здоровья).

• Правильные звездчатые многогранники (тела Кеплера-Пуансо).

1. Тема 6. Природные многогранники (кристаллы).

• Форма алмаза-октаэдр, куб, кубооктаэдр.

• Исланский шпат-косой параллелепипед.

• Пирит-куб, октаэдр.

• Кристалл граната – ромбододекаэдр.

1. Тема 7. Моделирование многогранников

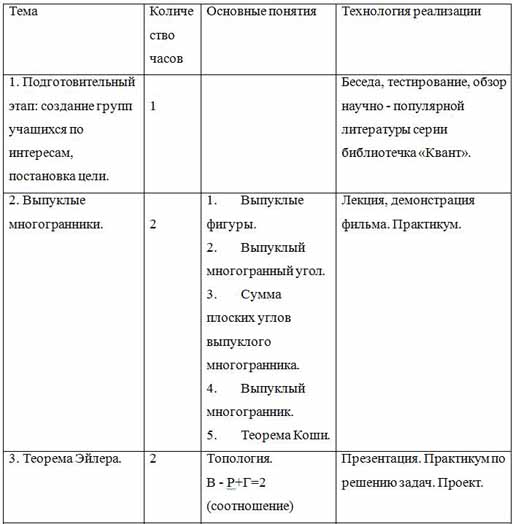
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА

3. Контрольно-оценочный блок

КРИТЕРИИ ОЦЕНКИ ПРОЕКТНО-ИССЛЕДОВАТЕЛЬСКИХ РАБОТ

(разработаны учителями математики ГБОУ СОШ с. Хворостянка)

1. Четкость постановки цели проекта.

2. Практическая направленность поставленных задач: изготовление продукта или усвоение теоретических знаний с целью использования их в повседневной жизни.

3. Оригинальность гипотез и их право на существование в социуме.

4. Грамотность математической речи.

5. Качество оформления работы, конечный продукт труда.

6. Эрудиция.

7. Разнообразие использованных технических средств.

8. Умение отвечать на вопросы оппонентов.

Каждый из перечисленных параметров оценивается 10 баллами.

60-80- труд высокого качества;

50-55- хороший труд;

30-49- удовлетворительный труд;

0-29- труд требует доработки.

КРИТЕРИИ ОЦЕНКИ ПРАКТИЧЕСКИХ РАБОТ

Изготовление моделей многогранников.

1. Модель соответствует действительности.

2. Соблюдены наиболее оптимальные размеры (30 х 30)

3. Аккуратность и эстетичность.

КРИТЕРИИ ОЦЕНКИ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

1. Грамотно выполнен чертеж.

2. Приведена верная последовательность шагов решения.

3. Обоснованы ключевые моменты решения.

4. Все преобразования и вычисления выполнены верно. Получен правильный ответ.

4. Ресурсный блок (условия)

Учебно-методическая литература:

1. Программно-методические материалы. Геометрия 7-11. И.М. Смирнова.

2. Модели многогранников. М. Веннинджер. Мир. 1974 г

3. Геометрия 10-11 класс. И. М. Смирнова. Мнемозина, 2006 г.

4. Симметрия в науке и искусстве. Наука. 1972 г.

Материальные ресурсы:

Для реализации элективного курса «Многогранники» используем учебно-наглядный материал по математике по курсу «Геометрические фигуры», по географии «Коллекция полезных ископаемых», по химии «Коллекция минералов», ИТ- оборудование (ноутбуки с подключением Интернет, мультимедиапроектор, интерактивная доска), электронную библиотеку, телевизор, видеомагнитофон, цифровой микроскоп, документ-камера.

Для экскурсии предоставляется школьный автобус.

Организационные ресурсы: элективный курс проводится в рамках реализации профильного обучения в 10 классе, согласно учебному плану. Занятия проводятся по расписанию, имеется график консультаций по проекту.

III. Заключение

Выводы: Проектно-исследовательская деятельность, с точки зрения учащихся, – это возможность самостоятельно создать интеллектуальный продукт, максимально используя свои возможности; это - деятельность, позволяющая проявить себя, попробовать свои силы, приложить свои знания, принести пользу и публично показать результат, самоутвердиться.

Проектно-исследовательская деятельность, органично сочетаясь с другими технологиями и методиками, приводит к определенным результатам.

Получают развитие общих умений учащихся, а главное – проектно-исследовательские умения. Это: постановка задач, выдвижение гипотез, выбор методов решения, построение обобщений и выводов, анализ результата.

Учащиеся получают навыки работы в текстовом редакторе, редакторе формул, в построении чертежей геометрических фигур с помощью Word и Paint. Знакомятся с математическими программами на электронных носителях.

Учащиеся получают представление об общих требованиях к подготовке, проведению и оформлению учебной работы. Учатся оформлять проекты в виде презентаций в устной форме и на электронных носителях.

Проектно-исследовательская деятельность позволяет выявить творческие способности учащихся, их деловые качества.

С целью наибольшего эффекта и минимизацию рисков я обязательно провожу рефлексию.

ЛИСТ РЕФЛЕКСИИ (составляется для каждого проекта)

IV. Информационные источники

1. Метод проектов в обучении математике. Е. Антонова. Математика №13. 2008 г

2. Практическая психодиагностика. Самара. 1998 г. Д. Я. Райгородский.

3. Я выбираю. Элективный курс. А. Ф. Дерезин. Ростов – на - Дону, 2007 г

4. Методические рекомендации для учителя. И.М. Смирнова. Мнемозина. 2003 г.

5. Профильное образование. Сборник элективных курсов. Математика 8-9 класс. М.Е.Козина. Волгоград.

6. Нетрадиционные формы организации тематического контроля на уроках. М.Е.Козина. Учитель. 2006 г.

7. Повышение эффективности обучения математике в школе. Книга для учителя. Из опыта работы. Г. Д. Глейзер. Просвещение. 1989 г.

Приложения №1

АНКЕТА

Диагностика «Хочу-могу-надо»

Ф.И._____________________________________________Класс____________

1. Задатки дарования есть у каждого человека, в соответствии с ними нужно выбрать профессию. Отметить тот признак одаренности, который проявляется у тебя в наибольшей мере: хорошая память; наблюдательность; сообразительность; тонкость и точность движений; тонкое обаяние; умение различать цвета и их оттенки; рассудительность; здравый смысл; устойчивый интерес ко всем наукам; высокая умственная работоспособность; увлеченность техникой; умение конструировать, моделировать; интерес к экспериментам; любовь к детям; страсть к путешествиям; желание много увидеть; любовь к природе, интерес к кулинарии; постоянно испытываемое удовольствие от общения.

2. Чем ты отличаешься от других? В чем твое превосходство, в чем отстаешь ты? __________________________________________________________________________________________________________________________________________________________________

3. Некоторыми профессиями невозможно овладеть при определенных недостатках, которые называются противопоказаниями к профессии. Перечисли их: аллергия на пищу, запахи; плохое здоровье; болезненность; быстрая утомляемость; повышенная нервная чувствительность; раздражительность; нетерпеливость; боязнь крови, человеческих страданий; вспыльчивость, неуравновешенность; быстрая утомляемость от общения с людьми; неаккуратность, неряшливость, небрежное отношение к работе и быту; отсутствие выдержки, конфликтность; нежелание переделывать плохо выполненную работу.

4. Подчеркни профессиональные черты человека, которые для тебя являются образцом: знание своего дела; вдумчивость; цепкость к работе; творческий склад ума; нестандартность мышления; умение быть простым, доступным в общении с людьми; требовательность к себе и своей работе; высокая результативность труда, его качество; умение учитывать условия и обстоятельства; умение преодолевать трудности; уверенность в своих силах.

5. Подчеркни требования к свое будущей профессии: отсутствие чрезмерной физической нагрузки, конкретные результаты, возможность творчества, возможность развивать способности, высокая зарплата, возможность заниматься любимым делом, общение с интересными людьми, высокая общественная значимость, разнообразие в содержании работы, свободное время, возможность самому регулировать рабочее время.

6. Какой учебный предмет является твоим любимым и почему?

Люблю­­­­________________________________________________(предмет), потому что он легко усваивается; развивает хорошо ум и способности; нравится преподаватель этого предмета; нравится, как преподают этот предмет; знание этого предмета необходимо для поступления в институт; знание этого предмета пригодится для будущей профессии.

Профессия или область деятельности, которые я выбрал _________________________________________________________________________________

Приложение №2

ЗАНЯТИЕ № 1 (1 час)

Подготовительный этап

Цель: создание групп учащихся по интересам, постановка общей цели курса.

Ход занятия:

1. Анкетирование.

2. Обработка результатов анкетирования.

3. Создание групп по интересам.

4. Знакомство с программой профильного курса.

ЗАНЯТИЕ № 2 (2 часа)

Тема: Выпуклые многогранники.

Цель: Знакомство с историей исследования многогранников, их видов. Показать учащимся геометрическую красоту фигур и использование их красоты форм в окружающем мире.

Ход занятия:

1. Экскурс в историю. Лекция учителя, просмотр фильма.

2. Лабораторная работа: «Определение вида многогранника». (Дается набор многогранников, нужно их распределить по группам).

3. Теорема Коши.

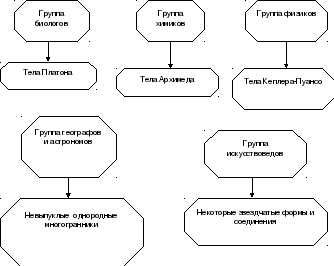
4. Невыпуклые однородные многогранники.

Результатом данного занятия будет: умение классифицировать многогранники.

ЗАНЯТИЕ № 3 (2час)

Тема: Теорема Эйлера.

Цель: Овладение учащимися историко-биографической информацией, касающихся Эйлера; выработка навыков в решении практических задач с использованием теоремы Эйлера.

Ход занятий:

1. Биографические сведения об ученом Эйлере.

2. История открытия формулы В-Р+Г=2

3. Понятие топологии.

4. Практикум по решению задач.

Результатом занятия будет: умение решать практические задачи.

ЗАНЯТИЕ № 4 (2час)

Тема: Правильные многогранники (Тела Платона)

Цель: Знакомство с понятием правильного многогранника, их видами, свойствами; выявление роли Тел Платона в географии, астрономии

Ход занятия:

1. Историческая справка: И.Кеплер «Тайна мироздания»

2. Презентация «Правильные многогранники»

3. Практикум по конструированию правильных многогранников.

Результатом работы будет игровой проект «Путешествие многогранника по страницам географии и астрономии».

ЗАНЯТИЕ № 5 (2час)

Тема: Полуправильные многогранники (Тела Архимеда). Псевдоархимедов многогранник.

Цель:

Ход занятий:

1. Лекция. Полуправильные, квазиправильные многогранники.

2. Историческая справка об учёном Архимеде.

3. Презентация «Полуправильные многогранники».

4. Практикум по решению задач.

5. Обсуждение статьи А. Рубцова об «открытии» полуправильного многогранника.

Результатом работы будет выпуск сборника задач «Многогранники».

ЗАНЯТИЕ № 6 (2час)

Тема: Звёздчатые многогранники.

Цель: Установить связь геометрии с искусством через звёздчатые многогранники.

Ход занятий:

1. Информационный проект «История открытия звёздчатых многогранников».

2. Основные способы их получения.

3. Звёздчатые многогранники в природе.

4. Практикум по изготовлению фигур.

Результатом работы будет информационный проект «Многогранник и искусство».

ЗАНЯТИЕ № 7 (2 часа)

Тема: Природные многогранники (кристаллы). Геометрические понятия в физике.

Цель: показать основополагающую роль многогранников в мироздании с точки зрения физических законов.

Ход занятия.

I Сообщения учащихся группы «физиков»:

а) отличительные черты кристаллического состояния;

б) кристаллы и их геометрия (красота, симметрия, гармония);

в) роль симметрии в создании картины мироздания;

г) закон Кеплера о постоянстве углов между гранями кристалла (работа «Новогодний подарок»);

д) симметричность физических законов (сдвиг, поворот);
е) кристаллы в электронике, радиотехнике, оптике, генной инженерии;

ж) законы Федорова.

II Просмотр фильма «Кристаллы в природе».

III Работа с коллекцией минералов.

Вывод: Законы, которым подчиняются кристаллы,- ориентир, настраивающий нашу мысль, наше зрение и слух на постижение мироздания, единства его многообразных форм.

ЗАНЯТИЕ № 8 ( 1 час )

Тема: Моделирование многогранников.

Цель: Знакомство с основными положениями по изготовлению моделей многогранников; практическое закрепление теоретических знаний; воспитание культуры труда.

Ход занятия

I Знакомство с книгой М.Веннинджера «Модели многогранников».

II Изучение инструкции по изготовлению моделей.

Инструкция № 1

Общие указания по изготовлению моделей (использованы

материалы М. Веннинджера).

1. Аккуратно вычерчивать нужные вам части. Для выпуклых многогранников ими будут только правильные многоугольники с 3, 4,5,6,8, и 10 сторонами. Но следует помнить, что у выпуклых однородных многогранников все ребра имеют одну и туже длину. Следовательно, все многоугольники, образующие один многогранник, должны иметь стороны одной и той длины.

2. Изготовить трафареты. Для этого наложите чертеж на лист картона или плотной бумаги и проколите оба листа в вершинах многоугольника тонким шилом. После этого соедините по линейке полученные проколы, воспользовавшись острым карандашом. Аккуратно и ровно вырежьте ножницами трафарет, оставляя поля, отстоящие от карандашной линии примерно на 0,5 см.

3. Изготовить столько его копий, сколько вам требуется.

4. Аккуратно подравнять ножницами края заготовки.

5. Для склеивания надо оставлять как можно больше места и срезать столько, сколько необходимо, чтобы наклейки не мешали одна другой и граням вблизи вершин.

6. Можете пользоваться любым клеем, лишь бы он не коробил заготовки.

7. В работе время от времени надо пользоваться пинцетами; они особенно полезны при завершении работы, когда модель приобретает окончательную форму. Хорошо иметь зажимы, необходимые для сложных моделей. Зажимы можно изготовить из пружины, между витками которой помещаются склеиваемые поверхности.

Практические задания получают все группы.

Инструкция № 2

Раскраска моделей

Любую модель многогранника можно раскрасить разнообразными способами. Какие же требования следует наложить на раскраску, чтобы выбрать из всевозможных вариантов один или несколько наилучших? Наиболее очевидные требования:

Используются и другие критерии выбора.

В подавляющем большинстве случаев используется один из следующих методов раскраски.

Принцип раскраски карт. Согласно принципу раскраски карт, любые две грани, имеющие общее ребро, должны иметь разные цвета. При такой раскраске границы между гранями хорошо видны. Необходимо отметить, что в невыпуклых многогранниках при следовании этому принципу одноцветные грани могут пересекаться. В соответствии с этим принципом удобно окрашивать выпуклые многогранники. В сложных невыпуклых многогранниках с большим числом пересекающихся граней следование принципу раскраски карт приводит либо к необходимости использования огромного числа цветов (несколько десятков), либо к тому, что имеется много одноцветных пересекающихся граней.

Принцип идентичных граней. В соответствии с принципом идентичных граней, однотипные грани окрашиваются в один цвет (даже если они имеют общие ребра); грани разных типов имеют разные цвета. Пример такой раскраски усеченного тетраэдра приведен на рисунке, шестиугольные грани имеют желтый цвет, треугольные - зеленый.

Принцип частей соединения. При окраске соединений нескольких многогранников может использоваться окраска, при которой каждый из многогранников окрашен в собственный цвет. На рисунке приведена подобная окраска многогранника Stella octangula, который может рассматриваться как соединение двух тетраэдров. Один из тетраэдров имеет красный, другой - оранжевый цвет.

Результатом работ должно быть изготовление моделей многогранников, установление их наличия в окружающем мире.

ЗАНЯТИЕ № 9 (1час)

Тема: Научно-практическая конференция учителей и учащихся «Многогранники как основа мироздания».

Цель: Подведение итогов практической и исследовательской деятельности учащихся.

Программа конференции

I Теоретическая часть.

1. Отчёт о результатах лабораторного эксперимента по выращиванию кристаллов: «Многогранник и химия».

2. Результаты информационного проекта «Многогранник и искусство».

II Практическая часть.

1. Демонстрация геометрических фигур – результат труда практической лаборатории.

2. Просмотр фильма, созданного группой учащихся, устанавливающих связь между геометрией и физикой: «Кристаллы в природе».

3. Деловая игра «Путешествие многогранника по страницам географии и астрономии».

III Заключительная часть.

Знакомство с творческими проектами учащихся: сочинения, стихи о значении многогранников.

IV Итог. Рекомендации.

20