Методическая разработка урока математики в 9 классе по теме:
«Методы решения систем уравнений с двумя переменными».
Данная работа представляет собой методическую разработку четвертого урока по теме «Методы решения систем уравнений с двумя переменными». Урок направлен на решение следующих задач: проверка знаний учащимися фактического материала, умений применять правила и пользоваться освоенными закономерностями, совершенствование вычислительных навыков; развитие навыков самостоятельности, самоконтроля, самооценки; адекватной оценки собственных знаний и навыков.
Материалы урока рассчитаны на учащихся 9 класса.
Каждый ученик в ходе урока выполняет определенные задания: устная работа, решение индивидуальных заданий, подготовка к ОГЭ, тестовая работа, результаты которой из бальной оценки переводятся в отметку, таким образом, осуществляется промежуточный контроль результатов.
На этом уроке формируются УУД учащихся: коммуникативные, регулятивные, познавательные.
Технологическая карта урока математики в 9 классе по теме «Методы решения систем уравнений с двумя переменными»
по учебнику Мордковича А.Г.
| ФИО | Манякова Вера Алексеевна | ||||||||||||||
| Место работы | МБОУ СОШ № 82 | ||||||||||||||
| Должность | Учитель математики | ||||||||||||||
| Предмет | Математика | ||||||||||||||
| Класс | 9 | ||||||||||||||
| Базовый учебник | А.Г. Мордкович, П.В. Семенов. – Алгебра. 9 класс. Учебник и задачник для учащихся общеобразоватльных учреждний. – 16-е изд., доп. – М.: Мнемозина, 2013. | ||||||||||||||
| Название урока | Методы решения систем уравнений с двумя переменными | ||||||||||||||
| Тип урока | Урок обобщения и систематизации знаний | ||||||||||||||
| Образовательная среда урока | Компьютер, проектор, учебники по математике, раздаточный материал, мел, доска, электронная презентация, выполненная в программе Power Point. | ||||||||||||||
| Формы работы учащихся | Фронтальная, индивидуальная. | ||||||||||||||
| Цель урока | Предметные | Личностные | Метапредметные результаты | ||||||||||||
|
| Знать: алгоритм решения систем уравнений: графическим способом; способом подстановки; способом сложения. Уметь: решать системы уравнений второй степени различными способами. Применять: полученные знания для решения систем уравнений различных уровней сложности. | определять личностный смысл деятельности; осуществлять выбор в соответствии с задачей деятельности. | Познавательные УУД: определять способы решения и обосновывать свое мнение; анализировать задачу, ситуацию; Регулятивные УУД: выполнять самопроверку и самооценку выполнения учебного задания; умение планировать и осуществлять деятельность, направленную на решение проблем различного характера. Коммуникативные УУД: предлагать и обосновывать своё мнение. | ||||||||||||
| Задачи урока: Образовательные - обобщение, систематизация и углубление знаний учащихся по изучаемой теме, формирование умений применять разные способы решения систем уравнений; Воспитательные - развитие творческих способностей учеников, привитие интереса к изучаемому предмету; Развивающие - формирование навыков самостоятельной деятельности, выработка внимания. | |||||||||||||||
| Этапы урока | Деятельность учителя | Деятельность ученика | Формируемые УУД | ||||||||||||
| Организационный (2мин) | Приветствие учащихся. Проверка учителем готовности класса к уроку; организация внимания. - Здравствуйте, садитесь! Начинаем наш урок. Сдайте пожалуйста тетради с домашней работой. | Слушают учителя, настраиваются на работу, проверяют готовность к уроку.
| Умение слушать и вступать в диалог. Умение выделять нравственный аспект поведения. | ||||||||||||
| Актуализация знаний, (10 мин) | Вступительное слово учителя. Вспомним, чем мы занимались на прошлом уроке? | Отвечают на вопрос. | Познавательные: применение предметных знаний; выполнение учебных заданий. Регулятивные: выделение и осознание того, что уже пройдено; умение распознавать на слух вопросы и отвечать на них. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. | ||||||||||||
| Индивидуальное задание | Для решения следующего индивидуального задания, необходимы двое учащихся. Задание: Решить систему равнений | Решают у доски. |
| ||||||||||||
| Актуализация знаний. | Ребята, давайте вспомним: А) Что называется решением системы уравнений?
Б) Что значит решить систему уравнений?
В) Дайте понятие равносильности двух систем уравнений?
Г) Какие методы решения систем уравнений вы знаете: | Отвечают у доски А) Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Б) Решить систему уравнений – значит найти все её решения или доказать, что решений нет. В) Две системы уравнений называются равносильными, если они имеют одни и те же решения, или если обе системы не имеют решений. Г) Графический метод, подстановки, алгебраического сложения, введения новой переменной. | Познавательные: структурирование знаний, выбор способов решения задач, анализ объектов и синтез. Регулятивные: умение проговаривать последовательность действий на уроке, Коммуникативные: развитие умения слушать и вступать в диалог, задавать вопросы. Личностные: осуществлять выбор в соответствии с задачей деятельности. | ||||||||||||
|
| 1) Попробуем определить, какой из этих способов лучше применить в каждом из следующих заданий:
- Какой недостаток имеет графический метод решения систем уравнений.
2) Рассмотрим вторую систему: Какой метод решения вы бы предложили.
3) Рассмотрим следующую систему уравнений: Какой из методов позволяет упростить данную систему?
4) Сколько решений может иметь система уравнений?
| 1) в данном случае лучше применить графический способ, т.к. первое уравнение задаёт окружность с центром (-1; 2) и радиусом r=3. Графиком второго уравнения являются два луча, исходящие из точки (-1; -1). Данная система имеет 3 решения (-1; -1), (-4; 2) и (2;2).
- Этот метод ненадёжен, т.к. не всегда даёт точные ответы; поэтому полученные значения нужно проверять.
2) в данном случае лучше применить метод подстановки. Из второго уравнения выражаем 3) Методом алгебраического сложения получим
4) Прямая и окружность могут иметь две точки пересечения, одну или ни одной. Парабола и прямая могут иметь 2 общие точки, одну или ни одной. Гипербола и прямая пересекаются в 2 точках, в 1 или ни одной. | |||||||||||||
| Самостоятельная работа (12 мин) | Выполним самостоятельную работу. Условия заданий – на листочках, возьмите их, впишите фамилию. Первые пять заданий – с выбором ответа, шестое задание – практическая работа. Задания оцениваются в баллах.
Закончили. Возьмите карандаши и проверьте вашу работу. Если ответ верный, ставим «плюс», не верный- ставим» - минус». Подсчитайте количество полученных баллов и оцените себя в соответствии со шкалой перевода баллов в отметки. 10 баллов – «5» 8-9 баллов – «4» 5-7 баллов – «3» Поднимите руки, у кого получилось 8-10 баллов. Молодцы. Отложите работу. | Выполняют письменное задание в готовых бланках.
Учащиеся проверяют свой результат, выставляют отметку. | Познавательные: применение предметных знаний, выбор способов решения задач. Регулятивные: анализировать и оценивать результат работы; Личностные: самооценка. | ||||||||||||
| Физкультминутка (1 мин) | А сейчас немного отдохнём и выполним гимнастику для глаз. | Делают гимнастику. |
| ||||||||||||
| Проверка индивидуального задания. (4 мин) | Задание: Решить систему равнений 2) методом сложения. | 1 ученик – Я решала методом подстановки. Получив биквадратное уравнение, применила метод введения новой переменной. 2 ученик - Я решал эту систему с помощью формул сокращенного умножения. Применив метод сложения разбил систему на две более лёгкие системы. | Познавательные УУД: определение способа решения и обоснование своего мнения; Регулятивные УУД: умение планировать и осуществлять деятельность, направленную на решение задачи. Коммуникативные УУД: предлагать и обосновывать своё мнение. | ||||||||||||
| Работа с листами подготовки к ОГЭ (8 мин)
| А теперь разберем несколько заданий из 2 части сборника Лысенко. Открываем стр. 275, №163. Как будем решать данную систему.
А дорешаете эту систему вы дома.
Открываем стр. 306, №507.Решим задачу.
А дорешаете вы её дома.
Если успеем. Открываем стр. 276, №179. Решим систему уравнений.
| Разбирают задания вместе с классом. Делают пометки. Введём новые переменные
Получим:
Решая его, получим значения для m и n, и произведём обратную замену…
Пусть первый раствор имеет концентрацию m %, а второй раствор n %. Тогда получим систему…
Данную систему решаем с помощью формул сокращенного умножения (разности квадратов). | Познавательные: уметь решать примеры по выбранному правилу; ставить, формулировать и решать проблемы. Регулятивные: умение проговаривать последовательность действий на уроке, Коммуникативные: умение слушать, обращаться с вопросом к учителю и сверстнику. Личностные: навыки сотрудничества в разных ситуациях, самооценка. | ||||||||||||
| Домашнее задание | Дорешать номера №163, 507, 179 и решить №139, 141, 162 из сборника Лысенко. | Записывают домашнее задание. | Личностные: готовность и способность к саморазвитию; самооценка. | ||||||||||||
| Рефлексия. Подведение итогов урока (1мин) | На что был направлен наш урок? | 1) Урок был ориентирован на отработку навыков решения систем уравнения различными методами. 2) Разобрали задания из ОГЭ. | Познавательные: Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов. Регулятивные: Оценка-осознание уровня и качества усвоения. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли. Личностные: Ценностно-смысловая ориентация | ||||||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход



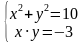 - 1) методом подстановки; 2) методом сложения используя формулы сокращённого умножения.
- 1) методом подстановки; 2) методом сложения используя формулы сокращённого умножения.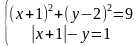
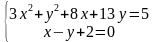
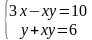 .
.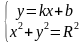 .
.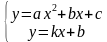 .
.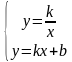
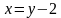 и подставив в первое уравнение, дорешиваем систему.
и подставив в первое уравнение, дорешиваем систему.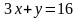 , выберем одно из этих уравнений, например 2, получим систему:
, выберем одно из этих уравнений, например 2, получим систему: 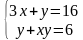 . А дальше решаем способом подстановки.
. А дальше решаем способом подстановки.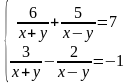
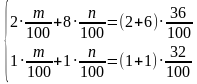
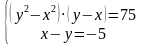
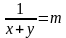
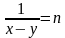
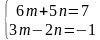









 Методы решения систем уравнений с двумя переменными (38.81 KB)
Методы решения систем уравнений с двумя переменными (38.81 KB)
 0
0 316
316 36
36 Нравится
0
Нравится
0


