Методика решения текстовых задач в 5-6 классах

Методика решения текстовых задач в 5-6 классах

Автор: Сидорова А.В., учитель математики

МБОУ г. Мурманска СОШ № 31

Математическая задача

– это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии.

Структура задачи

Любая текстовая задача состоит из двух частей: условия и требования (вопроса).

• В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними.
• Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме («Найти площадь треугольника.» или «Чему равна площадь прямоугольника?»).

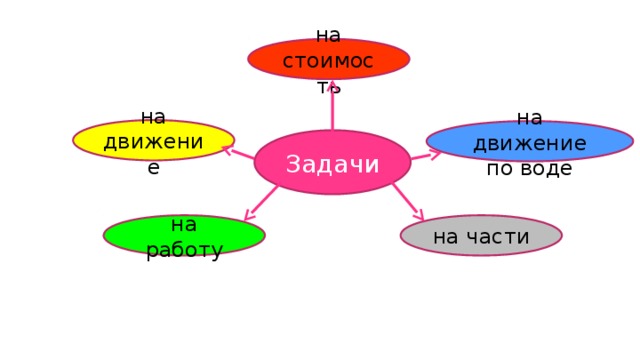
на стоимость

на движение

на движение по воде

Задачи

на работу

на части

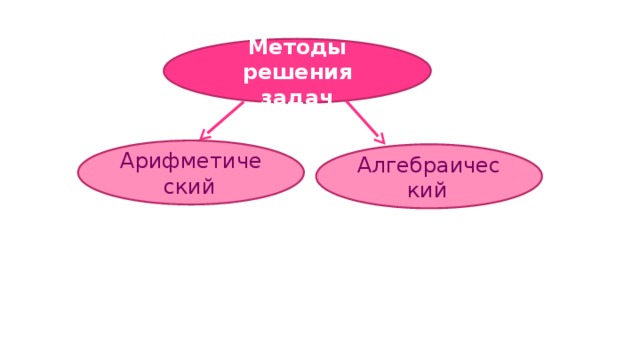
Методы решения задач

Арифметический

Алгебраический

Арифметический

• Найти ответ на требование задачи посредством выполнения арифметических действий над числами.
• Одну и ту же задачу можно решить различными способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи.
• Все арифметические задачи по числу действий, выполняемых для их решения, делятся на простые и составные.

Алгебраический

• Найти ответ на требование задачи, составив и решив уравнение или систему уравнений.
• Если для одной и той же задачи можно составить различные уравнения (системы уравнений), то это означает, что данную задачу можно решить различными алгебраическими способами.

Этапы решения задачи

• Анализ задачи
• Поиск плана решения задачи
• Осуществление плана решения задачи
• Проверка решения задачи

Анализ задачи

• Анализ - это метод рассуждений от искомых к данным.
• Основное назначение этого этапа – понять в целом ситуацию, описанную в задаче; выделить условия и требования; назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.

Специальные вопросы:

• О чём задача, т.е. о каком процессе (явлении, ситуации) идёт речь в задаче, какими величинами характеризуется этот процесс?
• Что требуется найти в задаче?
• Что обозначают те или иные слова в тексте задачи?
• Что в задаче известно о названных величинах?
• Что неизвестно?
• Что является искомым?

, чем На автобусе - ? км, на 128 км ? км О какой ситуации идёт речь в задаче ? Что в задаче известно о названных величинах? Что неизвестно? Что требуется найти в задаче? " width="640"

Группа туристов прошла пешком 72 км, проехала на поезде в 5 раз больше, чем прошла пешком, а на автобусе проехала на 128 км меньше, чем на поезде. Сколько километров прошли и проехали туристы?

Пешком – 72 км

На поезде - ? км, в 5 раз , чем

На автобусе - ? км, на 128 км

? км

О какой ситуации идёт речь в задаче ?

Что в задаче известно о названных величинах?

Что неизвестно?

Что требуется найти в задаче?

План решения задачи

• Как искать план решения текстовой задачи? Односложного ответа на этот вопрос нет.
• Одним из наиболее известных приёмов поиска плана решения задачи арифметическим способом является разбор задачи по тексту или по её вспомогательной модели.
• Разбор задачи проводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от её вопросов.

, чем На автобусе - ? км, на 128 км ? км 1) 72 ∙ 5 = 360 (км) – проехали на поезде Что надо знать, чтобы ответить на вопрос задачи? 2) 360 – 128 = 232 (км) – проехали на автобусе Что можно найти по условию задачи? Составим план действий. 3) 72 + 360 + 232 = 664 (км) Ответ: туристы прошли и проехали 664 км. " width="640"

Группа туристов прошла пешком 72 км, проехала на поезде в 5 раз больше, чем прошла пешком, а на автобусе проехала на 128 км меньше, чем на поезде. Сколько километров прошли и проехали туристы?

Каким образом можно проверить

правильность найденного решения?

Пешком – 72 км

На поезде - ? км, в 5 раз , чем

На автобусе - ? км, на 128 км

? км

1) 72 ∙ 5 = 360 (км) – проехали на поезде

Что надо знать, чтобы ответить на вопрос задачи?

2) 360 – 128 = 232 (км) – проехали на автобусе

Что можно найти по условию задачи?

Составим план действий.

3) 72 + 360 + 232 = 664 (км)

Ответ: туристы прошли и проехали 664 км.

, чем ? орехов на 23 , чем О какой ситуации идёт речь в задаче ? Что в задаче известно о названных величинах? Что неизвестно? Как можно перефразировать текст задачи? Что требуется найти в задаче? " width="640"

Три бельчонка Рыжик, Пушистик и Ушастик собирали орехи. Рыжик собрал 38 орехов, что на 16 меньше, чем Пушистик, а Ушастик на 23 ореха больше, чем Рыжик. Сколько всего орехов они собрали?

Рыжик – 38 ор.,

Пушистик - ? ор.

Ушастик - ? ор.,

на 16

, на 16 , чем

? орехов

на 23 , чем

О какой ситуации идёт речь в задаче ?

Что в задаче известно о названных величинах?

Что неизвестно?

Как можно перефразировать текст задачи?

Что требуется найти в задаче?

? г (х + 100 + 400) г , на 400 г ? г Что в задаче известно о количестве шерсти, израсходованной на каждую вещь? О какой ситуации идёт речь в задаче ? Каким способом будем решать задачу? Сколько всего израсходовали шерсти? Что обозначим за х? Зная, что всего израсходовали 1200 г шерсти, составляем уравнение: х + (х + 100) + (х + 500) = 1200 3х = 600 х + 500 = 200 + 500 = 700 (г) 3х + 600 = 1200 х = 600 : 3 Ответ: 700 г пошло на свитер. х = 200 3х = 1200 - 600 " width="640"

На шапку , шарф и свитер израсходовали 1200 г шерсти. Известно, что на шарф израсходовали на 100 грамм больше, чем на шапку, а на свитер – на 400 г больше, чем на шарф. Сколько граммов шерсти израсходовали на свитер?

Пусть х г израсходовали на шапку.

Шапка -

Шарф -

Свитер -

? г

х г

1200 г

1200 г

(х + 100) г

, на 100 г

? г

(х + 100 + 400) г

, на 400 г

? г

Что в задаче известно о количестве шерсти, израсходованной на каждую вещь?

О какой ситуации идёт речь в задаче ?

Каким способом будем решать задачу?

Сколько всего израсходовали шерсти?

Что обозначим за х?

Зная, что всего израсходовали 1200 г шерсти, составляем уравнение:

х + (х + 100) + (х + 500) = 1200

3х = 600

х + 500 = 200 + 500 = 700 (г)

3х + 600 = 1200

х = 600 : 3

Ответ: 700 г пошло на свитер.

х = 200

3х = 1200 - 600

, чем 2х 2х + 10 Зная, что в ящике стало в 5 раз больше, составляем уравнение: 3х = 60 2х = 2 ∙ 20 = 40(яб.) – было в ящике 5(х – 10) = 2х + 10 х = 60 : 3 5х – 50 = 2х + 10 Ответ: 20 и 40 яблок. х = 20 5х – 2х = 10 + 50 " width="640"

В корзине было в 2 раза меньше яблок, чем в ящике. После того, как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике?

Пусть х яблок было в корзине первоначально.

Корзина

Было

Изменилось

Ящик

Стало

х

х - 10

-10

+10

, в 5 раз , чем

2х

2х + 10

Зная, что в ящике стало в 5 раз больше, составляем уравнение:

3х = 60

2х = 2 ∙ 20 = 40(яб.) – было в ящике

5(х – 10) = 2х + 10

х = 60 : 3

5х – 50 = 2х + 10

Ответ: 20 и 40 яблок.

х = 20

5х – 2х = 10 + 50

Задачи на движение

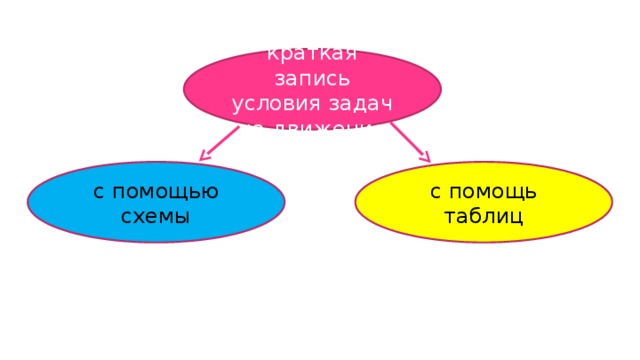
краткая запись условия задач на движение

с помощью схемы

с помощь таблиц

Алгоритм решения задач на движение

• Читаем задачу
• Выясняем, на какой вид движения эта задача
• По вопросу определяем, какой формулой эталона будем пользоваться

6 ? 156 О какой ситуации идёт речь в задаче ? Что требуется найти в задаче? Как, зная путь и время, найти скорость? 1) 276 : 4 = 69 (км/ч) – скорость ступы Как, зная путь и время, можно найти скорость? 2) 156 : 6 = 26 (км/ч) – скорость сапог - скороходов Какими величинами характеризуется этот процесс? 3) 69 – 26 = 43 (км/ч) Что в задаче известно о названных величинах? Что неизвестно? Ответ: на 43 км/ч скорость ступы больше. " width="640"

Отправившись в гости к Змею Горынычу, Баба-яга пролетела в своей ступе 276 км за 4 ч, а остальные 156 км за 6 ч в сапогах-скороходах. На сколько скорость движения ступы больше, чем скорость движения сапог-скороходов?

v = s : t

Вид транспорта

Ступа

S (км)

t (ч)

Сапоги-скороходы

v (км/ч)

?

4

276

на ?

6

?

156

О какой ситуации идёт речь в задаче ?

Что требуется найти в задаче?

Как, зная путь и время, найти скорость?

1) 276 : 4 = 69 (км/ч) – скорость ступы

Как, зная путь и время, можно найти скорость?

2) 156 : 6 = 26 (км/ч) – скорость сапог - скороходов

Какими величинами характеризуется этот процесс?

3) 69 – 26 = 43 (км/ч)

Что в задаче известно о названных величинах?

Что неизвестно?

Ответ: на 43 км/ч скорость ступы больше.

Двигаясь по пустыне в течение трёх дней, караван преодолел 63 км. В первый день караван двигался 6 ч, во второй – 8 ч, а в третий – 7 ч. Сколько километров проходил караван каждый день, если известно, что он двигался все дни с постоянной скоростью?

I день

v (км/ч)

t (ч)

II день

S (км)

III день

Пусть со скоростью х км/ч

двигался караван.

6

х

6х

Зная, что за три дня караван

преодолел 63 км, составляем

уравнение:

63 км

х

8х

8

х

7х

7

6х + 8х + 7х = 63

6х = 6 ∙ 3 = 18 (км) – прошёл в первый день

21х = 63

8х = 8 ∙ 3 = 24 (км) – прошёл во второй день

х = 63 : 21

7х = 7 ∙ 3 = 21 (км) – прошёл в третий день

х = 3

Ответ: 18 км, 24 км, 21 км.

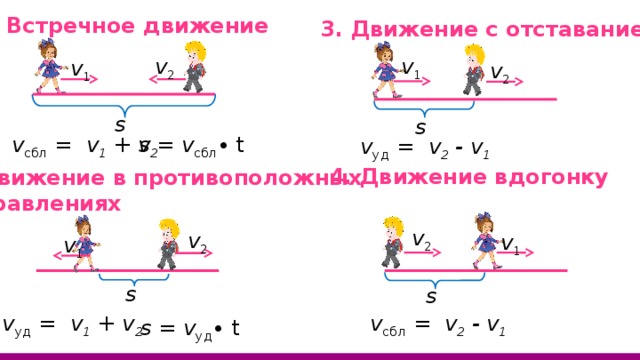
1. Встречное движение

3. Движение с отставанием

v 1

v 2

v 1

v 2

s

s

v сбл = v 1 + v 2

s = v сбл ∙ t

v уд = v 2 - v 1

4. Движение вдогонку

2. Движение в противоположных

направлениях

v 2

v 2

v 1

v 1

s

s

v уд = v 1 + v 2

v сбл = v 2 - v 1

s = v уд ∙ t

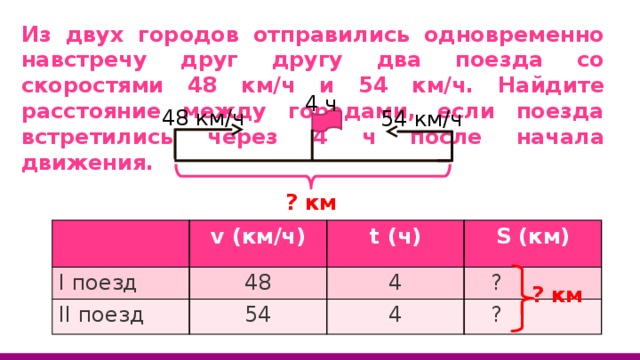
Из двух городов отправились одновременно навстречу друг другу два поезда со скоростями 48 км/ч и 54 км/ч. Найдите расстояние между городами, если поезда встретились через 4 ч после начала движения.

4 ч

48 км/ч

54 км/ч

? км

I поезд

v (км/ч)

II поезд

t (ч)

48

S (км)

4

54

?

4

?

? км

Из пунктов А и В, расстояние между которыми 60 км, одновременно навстречу друг другу отправились пешеход и велосипедист. Скорость пешехода 5 км/ч, а велосипедиста в 3 раза больше скорости пешехода. Какое расстояние будет между ними через 2 часа?

? км/ч

5 км/ч

? км

В

А

2 ч

2 ч

60 км

О какой ситуации идёт речь в задаче?

1) 5 ∙ 2 = 10 (км) – прошёл за 2 часа пешеход

2) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста

Что известно о скорости пешехода и велосипедиста?

3) 15 ∙ 2 = 30 (км) – проехал за 2 часа велосипедист

Сколько часов они были в пути?

4) 10 + 30 = 40 (км) – преодолели вместе за 2 часа

Что надо найти в задаче?

Ответ: 20 км.

5) 60 - 40 = 20 (км) будет между ними через 2 часа

Что требуется найти в задаче? О какой ситуации идёт речь в задаче? 1) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста Какими величинами характеризуется этот процесс? 2) 5 + 15 = 20 (км/ч) – скорость сближения Они сближаются или удаляются? 3) 60 : 20 = 3 (ч) Сколько километров преодолел каждый до встречи? Как найти скорость сближения при встречном движении? Что известно про скорости пешехода и велосипедиста? Как можно найти время, через которое они встретятся? Ответ: они встретятся через 3 часа. Что можно сказать про время движения пешехода и велосипедиста? " width="640"

Из пунктов А и В, расстояние между которыми 60 км, одновременно навстречу друг другу отправились пешеход и велосипедист. Скорость пешехода 5 км/ч, а велосипедиста в 3 раза больше скорости пешехода. Через сколько часов они встретились?

S (км)

пешеход

v (км/ч)

велосипедист

t (ч)

5

?

?

одинаковое

60

?

?

?, в 3 р.

Что требуется найти в задаче?

О какой ситуации идёт речь в задаче?

1) 5 ∙ 3 = 15 (км/ч) – скорость велосипедиста

Какими величинами характеризуется этот процесс?

2) 5 + 15 = 20 (км/ч) – скорость сближения

Они сближаются или удаляются?

3) 60 : 20 = 3 (ч)

Сколько километров преодолел каждый до встречи?

Как найти скорость сближения при встречном движении?

Что известно про скорости пешехода и велосипедиста?

Как можно найти время, через которое они встретятся?

Ответ: они встретятся через 3 часа.

Что можно сказать про время движения пешехода и велосипедиста?

Из одного пункта одновременно в противоположных направлениях отправились пешеход и велосипедист. Скорость велосипедиста в 3 раза больше скорости велосипедиста. Через 3 часа расстояние между ними стало 60 км. Найдите скорости пешехода и велосипедиста .

Пусть х км/ч скорость пешехода.

Тогда скорость велосипедиста – 3х км/ч.

Скорость удаления – (х + 3х) км/ч.

Зная, что они удалялись друг от друга за 3 ч,

на 60 км составляем уравнение:

3х км/ч

х км/ч

3 ч

3 ч

60 км

(х + 3х) ∙ 3 = 60

х = 5

4х ∙ 3 = 60

3х = 3 ∙ 5 = 15 (км/ч) – скорость велосипедиста

12х= 60

Ответ: 5 км/ч и 15 км/ч.

х = 60 : 12

2) 1050 + 840 = 1890 (км) – пролетел самолёт за 3 ч 3) 1890 : 3 = 630 (км/ч) – скорость самолёта Ответ: 630 км/ч. " width="640"

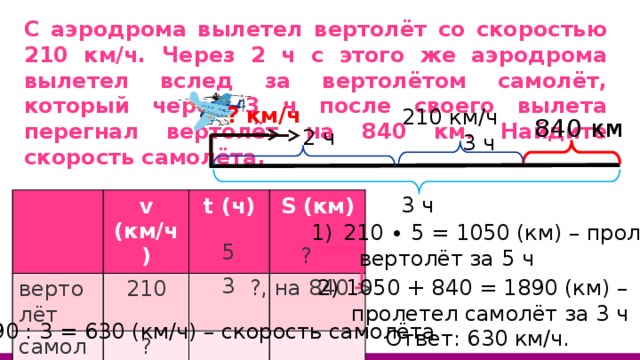
С аэродрома вылетел вертолёт со скоростью 210 км/ч. Через 2 ч с этого же аэродрома вылетел вслед за вертолётом самолёт, который через 3 ч после своего вылета перегнал вертолёт на 840 км. Найдите скорость самолёта.

? км/ч

210 км/ч

840 км

2 ч

3 ч

3 ч

v (км/ч)

вертолёт

210

t (ч)

самолёт

S (км)

?

• 210 ∙ 5 = 1050 (км) – пролетел

вертолёт за 5 ч

5

?

3

?, на 840

2) 1050 + 840 = 1890 (км) –

пролетел самолёт за 3 ч

3) 1890 : 3 = 630 (км/ч) – скорость самолёта

Ответ: 630 км/ч.

С аэродрома вылетел вертолёт со скоростью 210 км/ч. Через 2 ч с этого же аэродрома вылетел вслед за вертолётом самолёт, который через 3 ч после своего вылета перегнал вертолёт на 840 км. Найдите скорость самолёта.

? км/ч

210 км/ч

840 км

2 ч

3 ч

Пусть х км/ч скорость самолёта.

3 ч

Зная, что самолёт пролетел больше

на 840 км, составляем уравнение:

v (км/ч)

вертолёт

самолёт

t (ч)

210

S (км)

х

5

210 ∙ 5

3х – 1050 = 840

3

3х

Из двух пунктов навстречу друг другу выехали два автолюбителя, скорость одного из них 72 км/ч, а другого – 64 км/ч. Встретились они через 3 часа, а затем продолжили своё движение каждый по своему направлению. На каком расстоянии друг от друга будут автолюбители через 2 часа после встречи?

3 ч

72 км/ч

64 км/ч

• Какие данные в условии лишние?
• Поставьте другой вопрос к задаче и найдите на него ответ.
• Какой из автолюбителей будет ближе к своему конечному пункту от момента начала их движения?
• Какой из них будет ближе к своему конечному пункту от момента их встречи?

Движение по водному пути

Формулы

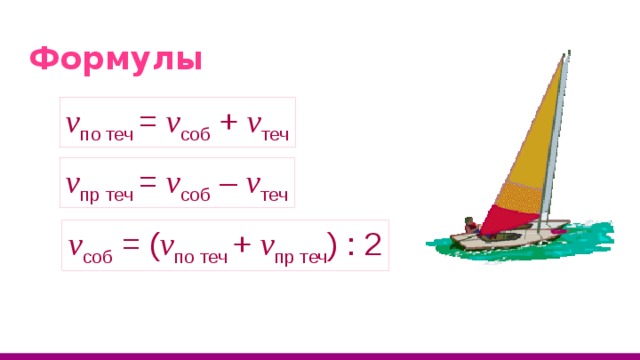
v по теч = v соб + v теч

v пр теч = v соб – v теч

v соб = ( v по теч + v пр теч ) : 2

Лодка может проплыть расстояние между двумя селениями, стоящими на берегу реки, за 4 часа по течению реки и за 8 часов против течения. Скорость течения реки 2 км/ч. Найдите собственную скорость лодки и расстояние между селениями.

Пусть х км/ч собственная скорость лодки.

Зная, что путь по течению и

против течения одинаковый,

составляем уравнение:

v (км/ч)

По течению

t (ч)

Против течения

S (км)

х + 2

4(х + 2)

4

4(х + 2) = 8(х – 2)

4х + 8 = 8х – 16

8(х – 2)

8

х - 2

4х – 8х = – 16 - 8

4(х + 2) = 4(6 + 2) = 32 (км)

- 4х = - 24

х= - 24 : (-4)

Ответ: собственная скорость лодки 6 км/ч,

расстояние между селениями 32 км.

х = 6

Памятка по решению текстовых задач

• Прочитайте задачу, попросите ребёнка представить себе то, о чём говорится в ней.
• Выясните у ребёнка, как он думает, что показывает каждое число, и попросите его выделить вопрос задачи.
• Предложите ему составить вспомогательную краткую запись условия задачи или зарисовать условие.
• Спросите его, можно ли сразу ответить на вопрос задачи. Если нет, то почему?
• Что нужно узнать сначала? Что потом?
• Предложите составить план решения задачи.
• Посоветуйте записать и выполнить решение.
• Проверить решение и записать ответ задачи предложите самостоятельно.

Из двух пунктов, расстояние между которыми 7 км 500 м, одновременно в одном направлении вышел пешеход со скоростью 6 км/ч и выехал автобус. Определите скорость автобуса, если он догнал пешехода через 15 минут.

Расстояние между двумя станциями 784 км. С этих станций одновременно навстречу друг другу вышли два поезда. Они встретились через 8 ч. Найдите скорость каждого поезда, если скорость первого на 10 км/ч больше скорости второго?