Материал по математике по теме "Методика подготовки учащихся решению задач на движение. ЕГЭ"

ВВЕДЕНИЕ

Математика проникает почти все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В связи с этим стало жизненно необходимым усовершенствовать математическую подготовку подрастающего поколения. С начала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснить различные стороны взаимосвязей в окружающей его жизни, даёт возможность применять изучаемые теоретические положения.

В «Федеральном компоненте образовательного стандарта основного общего образования по математике» представлен «обязательный минимум содержания основных общеобразовательных программ», среди которых есть и умение решать текстовые задачи.

Арифметика: «…Проценты. Нахождение процента от величины, величины по её проценту. Текстовые задачи (на движение, работу, стоимость, смеси и др.)Решение текстовых задач арифметическим способом»

Алгебра: «… Составление уравнений, неравенств и их систем по условиям задач. Решение задач алгебраическим способом».

В «Требованиях к уровню подготовки выпускников основной школы» сказано, что ученик должен уметь:

Арифметика: «, , , Решать текстовые задачи, включая задачи на движение и работу; задачи, связанные с отношением и с пропорциональностью величин; основные задачи на дроби и проценты; задачи с целочисленными неизвестными».

Алгебра: «, , , Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, учитывать ограничение целочисленности, диапазона изменения величин. »

В «Примерной программе основного общего образования по математике» дана «Общая характеристика учебного предмета», в которой отмечено, что «… одной из основных задач изучения алгебры является развитие алгоритмического мышления». А изучение основных типов текстовых задач и является одной из составляющих в развитии алгоритмизации мышления.

Состояние математического развития учащихся наиболее ярко характеризуется их умением решать задачи. Задачи – это основное средство оттачивания мысли каждого школьника. В процессе обучения решению задач ученики должны в известной мере овладевать основными идеями школьной математики, а именно:

- функциональной зависимости

- равенства, неравенства;

- тождественных преобразований;

- соответствия, порядка, расположения;

- непрерывности;

- доказуемости заключений относительно свойств пространственных форм и количественных соотношений в них;

- применимости числа и меры к явлениям окружающего мира.

Любая задача представляет собой требование или вопрос, на который надо ответить, опираясь и учитывая те условия, которые указаны в задаче.

Следует учесть, что научиться решать задачи школьники смогут, лишь решая их.

Решение задач занимает в математическом образовании огромное место. Поэтому обучению решения задач уделяется много внимания (уже в первом классе учащиеся начинают решать текстовые задачи). Связи с ведением ЕГЭ в 11 классе и экзаменом в новой форме в 9 классе умение решать текстовые задачи стало ещё более актуальным. Умение решать ту или иную задачу зависит от многих факторов. Однако, прежде всего необходимо научиться различать основные типы задач и уметь решать простейшие из них.

Без конкретной программы деятельности для учащихся, без алгоритмов или общих указаний по поиску решения задач, трудно организовать процесс учения детей, т. к. этот процесс имеет своими составными частями подражание и последующее творчество. Неосознанные навыки быстро утрачиваются. Лишь те навыки, которые доведены до автоматизма, или сохранили теоретическую основу, надолго остаются действенными. Я придерживаюсь в своей деятельности такого метода работы над задачами, когда ученик твёрдо усвоил основные приёмы решения задач и знает основные типы задач. Эти приёмы и способы задач вырабатываются в процессе изучения той или иной темы и только в последствии используются как алгоритм решения. Как показала практика, этот метод хорош при работе со слабыми и средними по успеваемости учениками. Они запоминают по различным признакам схему решения образца, решают определённый класс задач. Для более подготовленных учеников этот этап работы проходит быстро, без затруднений, они уже на начальной стадии изучения способны «ухватить» метод и применить его в более сложных задачах. Им даются уже более сложные задания, требующие не только автоматического применения основных приёмов, но и нетрадиционного подхода, смекалки.

В связи с переходом к новым формам аттестации учеников девятых и одиннадцатых классов формирование умений решать текстовые задачи стало ещё актуальным.

Объектом исследования является проблема обучения решению задач на движение при подготовке к ОГЭ, ЕГЭ.

Предметом исследования является разнообразие методических средств в процессе обучения решению задач на движение.

Цель – выявить методические особенности решения задач на движение в старших классах при подготовке к ОГЭ, ЕГЭ.

Задачи исследования:

1. изучить теоретико-методические особенности развития умения решать задачи,

2. проанализировать методические приемы решения задач на движение при подготовке к ОГЭ, ЕГЭ.

В процессе исследования использовались следующие методы: анализ психолого-педагогической и методической литературы по проблеме исследования; изучение специальной литературы по методике обучения математике в среднем звене школы; анализ современных отечественных программ обучения математике; систематизация полученной информации для проведения исследования.

Теоретическую основу исследования составили основополагающие идеи о педагогической деятельности в процессе обучения как о динамической педагогической системе, обоснованные в трудах Белошапко В. К., Бухаркиной М. Ю., Ершова А. П., Полат Е. С., о целях, структуре, средствах формирования и реализации процесса обучения математике в школе (Моисеева М. В., Соловов А. В. ).

Практическая значимость работы. Результаты исследования могут быть использованы в качестве методических рекомендаций к подготовке к ОГЭ, ЕГЭ в решении задач на движение.

Структура и основное содержание работы. Работа состоит из введения, двух глав, заключения и списка использованной литературы.

1. Теоретико-методические особенности развития умения решать задачи

1. 1. Алгоритм решения текстовых задач в школьном курсе

Одной из основных методических линий в курсе математики является линия обучения учащихся умению решать текстовые задачи. Реализуется эта линия с помощью специально сконструированной системы заданий. Выполняя эти задания, учащиеся могут увидеть, как то или иное математическое действие используется при разборе конкретных практических ситуаций. Разумеется, такая работа учеников предполагает и привлечение их опыта, накопленного в начальной школе. В традиционном российском школьном обучении математике текстовые задачи всегда занимали особое место.

Известно, что решение текстовых задач представляет большие трудности для учащихся. Известно и то, какой именно этап решения особенно труден. Это самый первый этап – анализ текста задачи. Учащиеся плохо ориентируются в тексте задачи, в ее условиях и требовании.

Полную информацию смотрите в файле.

Исследовательская работа

Тема: «Методика подготовки учащихся решению задач по теме «Задачи на движение», включенных в ОГЭ,ЕГЭ по математике»

Выполнила: Галимзянова В.В.

Должность: учитель математики

Место работы: «Средняя школа с углубленным изучением отдельных

предметов №62»

Авиастроительного района г.Казани

г. Казань-2015г.

СОДЕРЖАНИЕ

стр.

ВВЕДЕНИЕ 3

1. Теоретико-методические особенности развития умения решать задачи 7

1.1. Алгоритм решения текстовых задач в школьном курсе 7

1.2. Разбор решения задач В12 13

2. Методические приемы решения задач на движение при подготовке к ЕГЭ………………………………………………………………………………..17

2.1. Формирование умения решать задачи на движение 17

2.2. Урок по теме: «Решение текстовых задач при подготовке учащихся 11 класса к ОГЭ, ЕГЭ по математике» 22

ЗАКЛЮЧЕНИЕ 27

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 30

ВВЕДЕНИЕ

Математика проникает почти все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В связи с этим стало жизненно необходимым усовершенствовать математическую подготовку подрастающего поколения. С начала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснить различные стороны взаимосвязей в окружающей его жизни, даёт возможность применять изучаемые теоретические положения.

В «Федеральном компоненте образовательного стандарта основного общего образования по математике» представлен «обязательный минимум содержания основных общеобразовательных программ», среди которых есть и умение решать текстовые задачи.

Арифметика: «…Проценты. Нахождение процента от величины, величины по её проценту. Текстовые задачи (на движение, работу, стоимость, смеси и др.) Решение текстовых задач арифметическим способом»

Алгебра: «… Составление уравнений, неравенств и их систем по условиям задач. Решение задач алгебраическим способом».

В «Требованиях к уровню подготовки выпускников основной школы» сказано, что ученик должен уметь:

Арифметика: «,,, Решать текстовые задачи, включая задачи на движение и работу; задачи, связанные с отношением и с пропорциональностью величин; основные задачи на дроби и проценты; задачи с целочисленными неизвестными».

Алгебра: «,,, Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, учитывать ограничение целочисленности, диапазона изменения величин.»

В «Примерной программе основного общего образования по математике» дана «Общая характеристика учебного предмета», в которой отмечено, что «… одной из основных задач изучения алгебры является развитие алгоритмического мышления». А изучение основных типов текстовых задач и является одной из составляющих в развитии алгоритмизации мышления.

Состояние математического развития учащихся наиболее ярко характеризуется их умением решать задачи. Задачи – это основное средство оттачивания мысли каждого школьника. В процессе обучения решению задач ученики должны в известной мере овладевать основными идеями школьной математики, а именно:

• функциональной зависимости

• равенства, неравенства;

• тождественных преобразований;

• соответствия, порядка, расположения;

• непрерывности;

• доказуемости заключений относительно свойств пространственных форм и количественных соотношений в них;

• применимости числа и меры к явлениям окружающего мира.

Любая задача представляет собой требование или вопрос, на который надо ответить, опираясь и учитывая те условия, которые указаны в задаче.

Следует учесть, что научиться решать задачи школьники смогут, лишь решая их.

Решение задач занимает в математическом образовании огромное место. Поэтому обучению решения задач уделяется много внимания (уже в первом классе учащиеся начинают решать текстовые задачи). Связи с ведением ЕГЭ в 11 классе и экзаменом в новой форме в 9 классе умение решать текстовые задачи стало ещё более актуальным. Умение решать ту или иную задачу зависит от многих факторов. Однако, прежде всего необходимо научиться различать основные типы задач и уметь решать простейшие из них.

Без конкретной программы деятельности для учащихся, без алгоритмов или общих указаний по поиску решения задач, трудно организовать процесс учения детей, т.к. этот процесс имеет своими составными частями подражание и последующее творчество. Неосознанные навыки быстро утрачиваются. Лишь те навыки, которые доведены до автоматизма, или сохранили теоретическую основу, надолго остаются действенными. Я придерживаюсь в своей деятельности такого метода работы над задачами, когда ученик твёрдо усвоил основные приёмы решения задач и знает основные типы задач. Эти приёмы и способы задач вырабатываются в процессе изучения той или иной темы и только в последствии используются как алгоритм решения. Как показала практика, этот метод хорош при работе со слабыми и средними по успеваемости учениками. Они запоминают по различным признакам схему решения образца, решают определённый класс задач. Для более подготовленных учеников этот этап работы проходит быстро, без затруднений, они уже на начальной стадии изучения способны «ухватить» метод и применить его в более сложных задачах. Им даются уже более сложные задания, требующие не только автоматического применения основных приёмов, но и нетрадиционного подхода, смекалки.

В связи с переходом к новым формам аттестации учеников девятых и одиннадцатых классов формирование умений решать текстовые задачи стало ещё актуальным.

Объектом исследования является проблема обучения решению задач на движение при подготовке к ОГЭ, ЕГЭ.

Предметом исследования является разнообразие методических средств в процессе обучения решению задач на движение.

Цель – выявить методические особенности решения задач на движение в старших классах при подготовке к ОГЭ, ЕГЭ.

Задачи исследования:

1. изучить теоретико-методические особенности развития умения решать задачи,

2. проанализировать методические приемы решения задач на движение при подготовке к ОГЭ, ЕГЭ.

В процессе исследования использовались следующие методы: анализ психолого-педагогической и методической литературы по проблеме исследования; изучение специальной литературы по методике обучения математике в среднем звене школы; анализ современных отечественных программ обучения математике; систематизация полученной информации для проведения исследования.

Теоретическую основу исследования составили основополагающие идеи о педагогической деятельности в процессе обучения как о динамической педагогической системе, обоснованные в трудах Белошапко В.К., Бухаркиной М.Ю., Ершова А.П., Полат Е.С., о целях, структуре, средствах формирования и реализации процесса обучения математике в школе (Моисеева М.В., Соловов А.В.).

Практическая значимость работы. Результаты исследования могут быть использованы в качестве методических рекомендаций к подготовке к ОГЭ, ЕГЭ в решении задач на движение.

Структура и основное содержание работы. Работа состоит из введения, двух глав, заключения и списка использованной литературы.

1. Теоретико-методические особенности развития умения решать задачи

1.1. Алгоритм решения текстовых задач в школьном курсе

Одной из основных методических линий в курсе математики является линия обучения учащихся умению решать текстовые задачи. Реализуется эта линия с помощью специально сконструированной системы заданий. Выполняя эти задания, учащиеся могут увидеть, как то или иное математическое действие используется при разборе конкретных практических ситуаций. Разумеется, такая работа учеников предполагает и привлечение их опыта, накопленного в начальной школе. В традиционном российском школьном обучении математике текстовые задачи всегда занимали особое место. ⁰

Известно, что решение текстовых задач представляет большие трудности для учащихся. Известно и то, какой именно этап решения особенно труден. Это самый первый этап – анализ текста задачи. Учащиеся плохо ориентируются в тексте задачи, в ее условиях и требовании.

Текст задачи – это рассказ о некоторых жизненных фактах.

В тексте важно все: и действующие лица, и их действия, и числовые характеристики. При работе с математической моделью задачи (числовым выражением или уравнением) часть этих деталей опускается. Надо именно и научить умению абстрагироваться от некоторых свойств и использовать другие. Умение ориентироваться в тексте математической задачи – важный результат и важное условие общего развития ученика. И заниматься этим можно и не только на уроках математики, но и на уроках чтения и изобразительного искусства.

Структурную схему задачи мы представляем следующим образом:

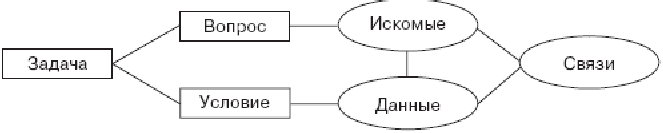
Каждая задача может быть охарактеризована по основным компонентам: условию, вопросу, базису, способу решения. В соответствии с этим система заданий для учащихся 5—6 классов содержит не только традиционные задачи (с полным набором данных, с поставленным вопросом, с указанием базиса, т. е. с указанием раздела математики, знание которого требуется для решения задачи, и т. д.), но и задачи с недостающими, лишними и противоречивыми данными, а также задачи, связанные с изменением условия или вопроса, задания на составление задач и т. д.

Например, в задаче в условии не хватает данных — учащиеся должны отметить, что время поездки складывается не только из времени, потраченного на остановки, но и из времени движения автомашины.

Вопрос: «Нет ли лишних данных?» возвращает учащихся к условию, требует вчитаться в текст, выявить лишние данные и найти рациональный способ решения.

Процесс решения задачи предполагает развитие у учащихся комплекса умений. Перечислим некоторые из них. ⁰

1. Анализ текста задачи:

1) внимательное чтение задачи;

2) первичный анализ текста: выделение вопроса задачи и ее условия;

3) оформление краткой записи текста задачи;

4) выполнение чертежей, рисунков по тексту задачи.

2. Поиск способа решения задачи:

1) проведение вторичного (более детального) анализа текста задачи: выделение данных и искомых, установление связей между данными, между данными и искомыми;

2) выяснение полноты постановки задачи;

3) осуществление поиска решения, составление плана решения задачи;

4) перевод словесного текста задачи на математический язык;

5) привлечение теоретических знаний для решения задачи.

3. Оформление найденного способа решения задачи:

1) оформление решения;

2) запись результата решения задачи.

4. Изучение найденного решения задачи:

1) контроль решения задачи;

2) оценка результатов решения;

3) анализ способов решения и их обобщение;

4) составление новых задач.

При обучении математике в 5 классе с целью формирования умения решать задачи особенно пристальное внимание следует уделить первому этапу, на котором формируется умение анализировать текст задачи.

Работа на первом этапе начинается с того, что ученики должны изучить условие задачи, которую они собираются решать, овладеть теми понятиями, на которые они будут опираться при ее решении, осознать цель и выбрать способ решения. Как показывает практика, некоторые учащиеся при встрече с задачей, не вчитавшись основательно в текст, сразу пытаются ее решать. Неумение учащихся читать текст и является первой причиной затруднений в решении задач. Поэтому первое, что должен делать учитель, — учить школьников «входить» в условие задачи и свободно ориентироваться в нем, учить читать и вчитываться в условие. ⁰

Учителю необходимо добиваться, чтобы учащиеся читали текст правильно, без искажения слов, с надлежащими остановками. Задача учителя — помочь учащимся выделить главное в тексте задачи, используя для этого различные формы предъявления задачи: текст, краткую запись, рисунок, чертеж.

Например, задача представлена текстом, схематической краткой записью, чертежом и рисунком. Сравнивая текст этой задачи и ее наглядное представление, учащиеся убеждаются, что главное в решении — найти целое по его частям.

Успех решения задачи во многом зависит от понимания учащимися смысла слов, входящих в текст задачи. В процессе чтения текста не все данные, входящие в условие, в равной степени привлекают внимание. В тексте задачи можно выделить слова, которые не влияют на выбор действия, и слова, которые влияют на способ решения задачи.

Важно научить учащихся «переводить» слова текста задачи на язык математических терминов, прямо указывающих на нахождение выбора действия. Учащиеся должны понимать, что отдельно взятое слово само по себе не определяет выбора действия, что следует учитывать сочетание слов и их последовательность расположения в тексте задачи.

Формированию умений находить слова, определяющие способ решения задачи, находить существенные связи, отвлекаться от сюжетных подробностей способствует такой прием, как изменение числовых данных задачи, математических и сюжетных связей. ⁰

Следующий шаг на этапе работы по анализу текста задачи — разбиение текста задачи на вопрос и условие. Обучение проведению первичного анализа текста задачи, предполагающего выделение условия и вопроса, их соотнесение тоже один из специальных приемов работы над текстом задачи. Этому помогут задачи, различающиеся по характеру формулировки вопросов и по месту их расположения.

Таким образом, формирование умений выделять условие и вопрос задачи предполагает прежде всего воспитание потребности выделять условие и вопрос задачи. Это может осуществляться в процессе нахождения необходимых данных для ответа на вопрос задачи, формулирования всевозможных вопросов к условию задачи, составления задачи по ее вопросу.

Анализируя работы учащихся, следует акцентировать их внимание на то, что по одному и тому же вопросу можно составить различные задачи.

Учителю следует показать учащимся, что при решении задачи ее вопрос определяет все последующие преобразования исходных данных. Так, например, методический прием — переформулирование вопроса сразу изменяет весь последующий процесс решения задачи.⁰

При обучении учащихся умению выделять условие и вопрос задачи в процессе ее решения следует использовать прием постановки вопроса задачи по ее условию. В ходе проведения первичного анализа там, где это необходимо и целесообразно, может быть оформлена краткая запись задачи. Собственно говоря, краткая запись задачи и является результатом проведенного первичного анализа текста задачи.

Краткая запись служит не только хорошей формой, организующей глубокий и планомерный анализ задачи, но и хорошим средством для понимания содержания задачи, зависимости между данными и искомыми, для облегчения поиска путей решения задачи. Это способствует не только решению конкретной задачи, но и обучению решению задач вообще.

Одним из способов выполнения краткой записи может быть таблица. Оформление краткой записи в виде таблицы используется в тех случаях, когда в задаче содержатся сведения об изменении трех взаимосвязанных величин. Данные и искомые при заполнении таблицы следует расположить так, чтобы яснее была выражена связь между ними. Наименование величины может быть внесено в столбец. Запись вопроса выполняется по возможности вне таблицы. Например, в задаче полезно сразу в процессе чтения заполнять таблицу

При решении задачи нередко используется прием оформления краткой записи в виде схемы для всей задачи или лишь для части ее условия. В схематической записи задачи должны быть отражены лишь самые необходимые сведения из условия задачи, она должна содержать общепринятые символы и сокращения.

В задаче путь, проделанный теплоходом, состоит из двух частей: по озеру и по реке. Для того чтобы найти расстояние, надо знать скорость и время. Время движения известно, скорость теплохода по озеру известна, а скорость по реке нет.

Краткую запись можно сделать так: (заготовка таблицы на экране)

Решение:

1. Найдем расстояние по озеру 23·3=69 (км)

2. Найдем скорость по реке 23+3=26 (км/ч)

3. Найдем расстояние по реке 26 * 4 =104 (км)

4. Найдем все пройденное теплоходом расстояние 69 +104=173 (км)

Полезен прием установления соответствия между краткой записью и текстом задачи. Учащиеся анализируют связь краткой записи с данным текстом задачи, выясняют связи между данными и искомыми задачи, вникая в каждое ее слово.⁰

Так как оформление рисунков, чертежей является хорошим средством обучения учащихся решению задач, то мы достаточно широко используем задания, требующие выполнения чертежей, рисунков по тексту задачи, чтения готовых чертежей, выполненных по тексту задачи, составления текста задач по готовым чертежам.

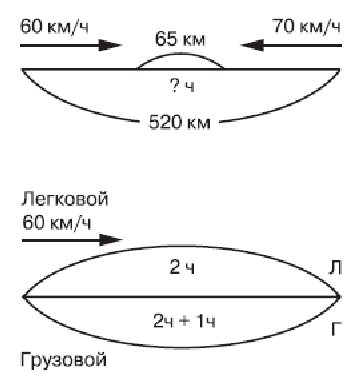
Выполняя чертеж к задаче, учащиеся замечают, что путь грузового и легкового автомобилей одинаков. Поэтому для решения задачи достаточно составить числовое выражение 60 = 2 : 3

1.2. Разбор решения задач В12

Задания типа В12 можно разделить на три основные группы задач по данной теме:⁰

I) задачи на движение;

II) задачи на производительность;

III) задачи на проценты, концентрацию, части, доли.

I. Основными типами задач на движение являются следующие:

1) задачи на движение по прямой (навстречу и вдогонку);

2) задачи на движение по замкнутой трассе;

3) задачи на движение по воде;

4) задачи на среднюю скорость;

5) задачи на движение протяжённых тел.

1. Движение навстречу

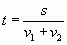
1) Расстояние между городами А и В равно 580 км. Из города А в город В со скоростью 80 км/ч выехал автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Через сколько часов после выезда второго автомобиля автомобили встретятся?

Решение:

1) 80*2=160(км) – проехал первый автомобиль

2) (580-160)/(80+60)=3(ч)

Ответ: 3

2. Движение вдогонку

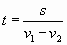
2) Два пешехода отправляются из одного и того же места в одном направлении на прогулку по аллее парка. Скорость первого на 1 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 200 метрам?

Решение:

200м = 0,2 км.; 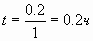; 0, 2 часа=12 минут

Ответ: 12.

3. Движение по окружности (замкнутой трассе)

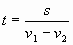
3) Из одной точки круговой трассы, длина которой равна 10 км/ч, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение:

Пусть скорость второго автомобиля х км/ч. Так как 40 минут = 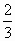часа и это время, за которое первый автомобиль будет опережать второй на один круг, составим уравнение

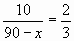; 30 = 180 – 2х; 2х = 150; х = 75

Ответ: 75.

4. Движение по воде

4) От лесоповала вниз по течению реки движется со скоростью 3 км/ч плот. Плотовщик доплывает на моторке из конца плота к его началу и обратно за 16 минут 40 секунд. Найдите длину плота, если собственная скорость моторки равна 15 км/ч. Ответ дайте в километрах.

Решение:

Пусть длина плота х км. Тогда скорость моторки по течению 18 км/ч, а против течения 12 км/ч. Так как 16 минут 40 секунд =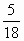часа, то

;

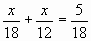2х + 3х = 10;

5х = 10;

х = 2.

Ответ: 2

5. Средняя скорость (слайд 4)

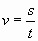
5) Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолёте со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

Решение:

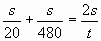
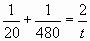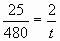; ; 25t=960; t= 38,4

Ответ: 38,4.

6. Движение протяжённых тел.

6) Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.

Решение:

65-5 =60 (км/ч)

60 км/ч=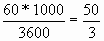м/с

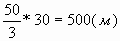
Ответ: 500.

На первом этапе достаточно подвести школьников к идее решения этой задачи с различными недостающими данными (собственная скорость и скорость течения) — это может быть хорошим домашним заданием. На следующем уроке можно будет подвести итог. Только не нужно делать вид, что совпадение результатов при различных значениях собственной скорости и скорости течения что-либо доказывает. Оно лишь подтверждает предположение «время движения туда и обратно одинаково».

2. Методические приемы решения задач на движение при подготовке к ЕГЭ

2.1. Формирование умения решать задачи на движение

С учетом современных подходов к математическому образованию возрастает социальная значимость математики, как средства повышения интеллектуального уровня человека; усиливается гуманитарная ориентация, происходит переориентация с увеличения количества информации на формирование умения анализировать ее, продуцировать, использовать; математика рассматривается как главное средство развития абстрактного мышления человека.

Поэтому, главная функция обучения математике – формирование умения решать задачи: ⁰

• задачи являются главным средством индивидуализации обучения;

• в ходе самостоятельного размышления над задачей происходит развитие учащегося;

• умение решать задачи является главным критерием успешности обучения математике;

• в ходе решения задач идет диалог ученика с учителем;

• самостоятельная деятельность по решению задач ограничивает сферу пассивных форм обучения.

В основе системы лежат идеи технологии укрупнения дидактических единиц (УДЕ) П.М.Эрдниева.

1. “ Метод обратных задач ” - в его основе идея обращения упражнений.

Суть метода: работу с задачей нецелесообразно завершать получением ответа; надо приемом обращения составлять и решать новую, обратную задачу, извлекая тем самым дополнительную информацию, заключающуюся в связях между величинами решенной исходной задачи.

Схема составления обратной задачи: исключая одно из чисел условия и делая его искомым, ответ исходной задачи вводим в обратную задачу в качестве известного.

Например, из пунктов A и B одновременно навстречу друг другу выехали автобус и легковой автомобиль. Скорость автобуса 55км/ч, а легкового автомобиля на 15км/ч больше. Найти расстояние между пунктами A и B, если автобус и автомобиль встретились через 3 часа. Ответ: 375км.

Составляем таблицу данных для исходной и обратных задач:

Формулируем и решаем обратные задачи.

Задача 1. Из пунктов A и B одновременно навстречу друг другу выехали автобус и легковой автомобиль. Скорость автобуса 55км/ч, а легкового автомобиля на 15км/ч больше. Расстояние между пунктами A и B равно 375км. Через сколько времени автомобиль и автобус встретились?

Задача 2. Из пунктов A и B, расстояние между которыми 375км, одновременно навстречу друг другу выехали автобус и легковой автомобиль и встретились через 3 часа. Скорость автобуса 55км/ч. На сколько скорость автобуса меньше скорости автомобиля?

Задача 3. Из пунктов A и B, расстояние между которыми 375км, одновременно навстречу друг другу выехали автобус и легковой автомобиль и встретились через 3часа. С какой скоростью ехал автобус, если известно, что его скорость на 15км/ч меньше скорости автомобиля?

Итак, при решении взаимно обратных задач учащийся выявляет и использует взаимно обратные связи между величинами, перестраивает суждения и умозаключения, использованные при решении прямой задачи. Обратные задачи – это продукт творчества учащегося, логическое продолжение прямой задачи. Составление и решение обратной задачи – один из путей саморазвития ученика.

2. Второй прием работы с задачами – самостоятельное составление школьниками упражнений на основе сравнения и обобщения, индукции и аналогии.⁰

В качестве иллюстрации обратимся к первой задаче, и будем менять ее условие, составляя и решая новые задачи.

- Изменим вопрос задачи: на каком расстоянии от пункта A встретились автобус и автомобиль?

- Изменим условие одновременного выхода: автомобиль выехал на час раньше автобуса.

Формулируем задачу. Выясняется, что необходимо указать момент отсчета времени.

Задача. Из пунктов A и B навстречу друг другу выехали автобус и легковой автомобиль.

Скорость автобуса 55км/ч, а автомобиля на15км/ч больше. Найти расстояние между пунктами A и B, если автобус выехал на час позже автомобиля и встретился с ним через 3 часа после своего выхода.

- Изменим условие встречного движения на движение в противоположных направлениях.

Задача. Из пунктов A и B, расстояние между которыми 100км, одновременно в противоположных направлениях выехали автобус и автомобиль. Скорость автобуса 55км/ч, а автомобиля на 15км/ч больше. Найти расстояние между ними через 3 часа.

- Изменим условие встречного движения на движение вдогонку.

Задача. Из пунктов A и B, расстояние между которыми 100км, одновременно в одном направлении выехали автобус и автомобиль. Скорость автобуса 55км/ч, а автомобиля на 15км/ч больше. Найти расстояние между ними через 3 часа.

Выясняется, что в этой задаче есть лишнее данное (55км/ч).

Для формирования умения решать задачи разрабатываю модули, состоящие из трех – четырех уроков. В качестве примера рассмотрим модуль “ Задачи на движение в противоположных направлениях ”.

Урок №1. Первый этап – тренинг-минимум, устно решаются простейшие задачи на нахождение скорости, времени, расстояния.

1

а) Пешеход за 3 часа прошел 12км. Сколько километров он проходил в час? Какова скорость пешехода?

б) Скорость велосипедиста 12км/ч. Сколько километров он проедет за 2 часа?

в) Скорость поезда 60км/ч. За какое время он проедет 180км?

Второй этап – решение задач на движение в противоположных направлениях, составление и решение обратных задач. К каждой задаче выполняется рисунок, демонстрирующий положение движущихся объектов на прямой в определенные моменты времени.

(Графическая модель движения ).

2.

а) Два пешехода вышли одновременно из одного пункта в противоположных направлениях. Скорость первого 4км/ч, второго 5км/ч. Покажите положение каждого пешехода через 1час, 2часа, 3часа. На каком расстоянии друг от друга они будут находиться через 1час, 2часа, 3часа? На сколько километров в час пешеходы удаляются друг от друга? ( Эту величину называют скоростью удаления ).

б) Из одного пункта в противоположных направлениях выехали две машины. Их скорости 60км/ч и 80км/ч. Определите скорость удаления машин.

в) Два поезда вышли одновременно из одной станции в противоположных направлениях. Скорость одного поезда 60км/ч, другого 70км/ч. Через сколько часов расстояние между ними будет 260км?

Урок №2. Первый этап – тренинг-минимум, устное решение задач на нахождение скорости, времени, расстояния и задач на движение в противоположных направлениях, аналогичных 2а), б), в). При этом максимально используются графические модели.

Второй этап – в задачу 2а) вводится усложнение: пешеходы выходят из пунктов A и B, расположенных на расстоянии 10км друг от друга. Решается задача и составляются три обратных.

Урок №3. Тренинг-минимум включает в себя устное решение задач, аналогичных 1, 2а), б), в), с максимальным использованием графических моделей.

Второй этап – в задачу 2а) вводится усложнение: один из пешеходов выходит в путь на 1час раньше другого. Формулируется и решается задача, составляются три обратных.

Третий этап – в задачу 2 вводятся два усложнения: пешеходы движутся из пунктов A и B, расположенных на расстоянии 10км друг от друга в противоположных направлениях, причем, один вышел в путь на 1час раньше второго.⁰

Следующий модуль содержит задачи на встречное движение.

3.

а) Из двух сел, расстояние между которыми 36км, одновременно навстречу друг другу вышли два пешехода. Их скорости 4км/ч и 5км/ч. На сколько километров в час пешеходы сближаются друг с другом? (Эту величину называют скоростью сближения). Какое расстояние будет между ними через 3 часа?

б) Два автомобиля движутся навстречу друг другу со скоростями 60км/ч и 80км/ч. Найдите скорость сближения автомобилей.

в) Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36км. Скорость первого велосипедиста 10км/ч, а второго – 8км/ч. Через какое время они встретятся?

4.

а) Расстояние между городами 900км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60км/ч и 80км/ч. На каком расстоянии друг от друга были поезда за час до встречи? Какое данное является лишним?

б) Расстояние от села до города 45км. Из села в город вышел пешеход со скоростью 5км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?

в) Два велосипедиста выехали одновременно навстречу друг другу из двух сел, расстояние между которыми 54 км, со скоростями 12 км/ч и 15 км/ч. Через сколько часов они будут находиться друг от друга на расстоянии 27км?

Модуль “Задачи на движение вдогонку” включает в себя работу с различными ситуациями движения двух объектов в одном направлении.

5.

а) Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, велосипедиста – 12 км/ч. Найдите скорость их удаления. Через какое время расстояние между ними составит 56 км?

б) Из двух пунктов, расстояние между которыми 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость одного из них 40 км/ч, второго – 50 км/ч. Через сколько часов второй мотоциклист догонит первого?

в) Из села вышел пешеход со скоростью 4 км/ч. Через 3 часа вслед за ним выехал велосипедист со скоростью 10км/ч. За сколько часов велосипедист догонит пешехода?

Подобная динамика работы с задачами, основанная на идеях укрупнения дидактических единиц, раскрывает и приводит в действие большие резервы человеческого мозга, развивает интеллектуальную сферу ученика.

2.2. Урок по теме: «Решение текстовых задач при подготовке учащихся 11 класса к ЕГЭ по математике»

Данный урок предлагается для проведения в 11 общеобразовательном классе в ходе итогового повторения.

На уроке решаются три типа текстовых задач, предлагавшихся выпускникам на ЕГЭ по математике. Это: задачи на совместную работу, задачи на части и задачи на арифметическую прогрессию.

Большая часть предлагаемых на данном уроке задач взята из реальных вариантов ЕГЭ по математике.

Для экономии времени тексты задач рекомендуется распечатать на отдельных листах и раздать учащимся, либо выводить при помощи проектора на экран.

1.Моторная лодка прошла 80 км от пункта А до пункта В и после трёхчасовой стоянки вернулась обратно, затратив на весь путь 12 часов .Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Пусть х км/ч – скорость лодки в неподвижной воде

80/(х+2)+80/(х-2)=12-3

9х^2-160х-36=0

х=-2/9 – не удовлетворяет условию задачи

х=18 км/ч

Ответ: 18.

2. Байдарка в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 45 минут, байдарка отправилась назад и вернулась в пункт А в 16:00 того же дня. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки равна 3 км/ч.

Решение: Легко понять, что плыла байдарка всего 16-10-1¹/₃₌4^2/₃ (ч)

Составим по условию задачи уравнение и решаем 15/(х+3)+15/(х-3)=14/3

14х²-90х-56=0

х₁=7 км/ч

х₂= -4/7 км/ч – не удовлетворяет условию задачи.

Ответ: 7

3. Из А в В одновременно выехали два автомобиля. Первый весь путь проехал с постоянной скоростью. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути – со скоростью 96 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 57 км/ч. Ответ дайте в км/ч.

Решение: Поскольку речь в задаче идёт о половинах пути, весь путь удобно принять за 2. Тогда половина пути 1 и х км/ч – скорость первого автомобиля.

2/х=1/(х-16)+1/96

х²-112х+32*96=0

х₁=64 км/ч х₂=48 км/ч

По условию подходит большее значение скорости, равное 64 км/ч.

Ответ: 64

4.Моторная лодка прошла против течения реки 120 км и вернулась в пункт отправления, затратив на обратный путь на 2 ч меньше времени. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.

Решение: Примем скорость лодки в неподвижной (стоячей) воде за х км/ч, тогда её скорость по течению (х+1) км/ч, а против течения (х-1) км/ч.

120/(х-1)-120/(х+1)=2

120(х+1)-120(х-1)=2(х²-1)

2х²-2=240

х=11

Ответ: 11.

5.Теплоход проходит по течению реки до пункта назначения 315 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 18 км/ч, стоянка длится 6 ч, а в пункт отправления теплоход возвращается через 42 ч после попытки из него. Ответ дайте в км/ч.

Решение: Скорость течения х км/ч. Скорость теплохода по течению (18+х) км/ч, а против течения – (18-х) км/ч

315/(18+х) – время теплохода по течению

315/(18-х) – время теплохода против течения

315/(18+х)+315/(18-х)=42-6

36х²-324=0

х²=9

х=3

Ответ: 3

6.Теплоход отошёл от пристани одновременно с плотом и прошёл вниз по реке 42 км. Сделав остановку на 1 час, он двинулся обратно вверх по реке. Пройдя 12 км, он встретился с плотом. Во сколько раз собственная скорость теплохода больше скорости течения реки, если скорость течения реки равна 4 км/ч?

Решение: х – собственная скорость теплохода

К моменту встречи теплохода с плотом плот прошёл 30 км за 30/4 =7,5 часов. Получаем уравнение: 42/(х+4)+1+12/(х-4)=7,5

13х²-108х+32=0

х₁=2,75

х₂ =8 По смыслу задачи скорость теплохода больше скорости течения, тогда скорость теплохода равна 8, то есть в 2 раза больше скорости течения.

Ответ: 2.

7. Велосипедист каждую минуту проезжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 ч больше, чем мотоциклист. Сколько километров в час проезжал мотоциклист?

Решение: х км/ч скорость мотоциклиста. Здесь нужно будут напомнить ученикам перевод м/мин в км/ч. Скорость велосипедиста на 800 м/мин меньше скорости мотоциклиста.

800 м/мин=800*60:1000=48 км/ч

Значит, (х-48) км/ч скорость велосипедиста.

30/(х-48)-30/х=2

х₁=-12 (не удовлетворяет)

х₂=60

Ответ: 60

8. Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал на 3 км/ч быстрее второго и прибыл к финишу на 3 часа раньше. Найдите скорость второго велосипедиста. Ответ дайте в км/ч.

Решение: х км/ч скорость второго велосипедиста, тогда (х+3) км/ч скорость первого велосипедиста. Зная, что они путь равен 130 км, составим уравнение:

130/х-130/(х+3)=3

х₁=-13(не удовлетворяет)

х₂=10

Ответ: 10

9. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали мотоциклист и велосипедист. Известно что за час мотоциклист проезжает на 30 км больше чем велосипедист. Узнать скорость велосипедиста если известно что он прибыл в пункт В на 1,5 часа позже мотоциклиста . Ответ дайте в км/ч.

Решение: Пусть х км/ч скорость велосипедиста, тогда 9х+30) км/ч скорость мотоциклиста. Велосипедист проехал 50 км за 50/х часов, а мотоциклист за 50/(х+3) часов, то есть на 1,5 часа быстрее. 1,5=3/2. Составим уравнение:

50/х-50/(х+30)=3/2

х=20

Ответ: 20

10. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

Решение: Время движения туда на 7 больше, чем время обратно (на время стоянки).

х км/ч – скорость из А в В

(х+7) км/ч скорость из В в А

98/х-98/(х+7)=7

14/х-14/(х+7)=1

х=7

Ответ:7

Итак, при решении задач на движение, используйте

Практические советы:

1. Записываем формулу-ключ: S = Vt

2. Определяемся с иксом, расписываем через икс все данные. Особое внимание на величины, входящие в формулу-ключ: путь, скорость, время. Эти величины – основа решения задач на движение. Стараемся снять всю возможную информацию с задачи.

3. До составления уравнения, приводим (если надо) все величины задачи к единым единицам измерения.

4. Записываем уравнение. Если никак не записывается, читаем задачу. Скорее всего, вы использовали не все данные из задачи или не увидели в тексте подсказки. Она, подсказка, всегда есть.

5. Решаем уравнение. При получении двух корней – за ответ берём приличный корень, несусветный и левый – отбрасываем.

ЗАКЛЮЧЕНИЕ

В данной работе были рассмотрены некоторые аспекты повышения эффективности процесса подготовки к ОГЭ,ЕГЭ при решении задач на движение. Результаты, полученные в ходе проведенного исследования, позволяют сделать следующие выводы.

На основе анализа литературы установлено, что, задачи на движение при подготовке к ОГэ,ЕГЭ являются наиболее сложными для учеников.

Особенности способа решения задач, усвоенного учащимися в процессе обучения, могут быть раскрыты через выделение ряда показателей, наиболее существенным, из которых являются: полнота предварительного семантического анализа текста задачи; наличие взаимосвязанных переходов от одного этапа решения к последующему, представляющих собой некоторое целостное образование.

Обучение решению текстовых задач на движение в курсе математики выполняет свою развивающую роль, прежде всего через формирование умения действовать со знаковыми замещениями реальных ситуаций, переводить их в знаковые образования иного рода и использовать при этом переводе (как его средство) выделение основных математических отношений.

Обобщенность и осознанность способа решения текстовых математических задач на движение в значительной мере достигается за счет деятельностного анализа его содержания и освоения через реализацию принципа трансформации компонентов деятельности на уровне "действие - операция".

Предлагаемый ниже Подход к решению текстовых задач сводится к двум основным моментам:

1) По условию любой задачи нужно обязательно (!) составлять рисунок. Именно так – как в 5-м классе! На него в схематичном виде наносится вся существенная информация. Достоинство такого рисунка – возможность одним взглядом охватить все содержание задачи и понять его, причем после его составления печатный текст условия для решения уже не нужен;

2) Рисунок позволяет выявить некий важный, ключевой факт (идею) решаемой задачи. По поводу этого факта заранее известно следующее:

Он обязательно содержится в условии;

Он очень простой;

Он может быть выражен «просто словами», без каких-либо формул;

Именно этот факт «порождает» уравнение, которое, в свою очередь, приводит к ответу (либо помогает вычислить искомое отношение).

Таким образом, рисунок дает быстрое понимание сути задачи, а найденный факт (идея) приводит к собственно решению.

Изучена методика работы над задачей на движение с помощью уравнений

• Через х обозначаем меньшую величину или то, о чём спрашивается в вопросе задачи.

• Краткую запись оформляем в виде таблицы, схемы.

• По условию задачи заполняем 2 столбика задачи, третий столбик заполняем, третий столбик нам даёт уравнение.

• Смотрим, к какому типу относится задача (на сложение величин, на сравнение и т.п.) в зависимости от этого составляем уравнение.

• Найдя х, смотрим, ответили мы на вопрос задачи, или нет, если нет, то решаем и находим ответ.

В результате изученной темы было выяснено, что существует множество различных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать условия задачи и решать их разными методами (путём составления уравнений и систем уравнений, путём составления таблиц и т. д.) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный -алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.

Данная проблема до конца не решена, необходимо искать новые формы, подходы, направления, новые методические обоснования для более успешного формирования умения решать текстовых задач.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Булынин В. Применение графических методов при решении текстовых задач// Математика, 2005, № 14.

2. Варшавский И.К., Гаиашвили М.Я., Глазков Ю.А. Текстовые задачи на Едином государственном экзамене. // Математика для школьников, №3, 2005

3. Высоцкий И.Р. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010. Математика / И.Р.Высоцкий, Д.Д.Гущин и др. – М.: «АСТ Астрель»,2010

4. Дорофеев В.Г. Математика для поступающих в ВУЗы; Пособие /В.Г.Дорофеев, Л.В. Кузнецова, Е.А.Седова – М.:Дрофа, 2001

5. Дорофеев Г.В., Потапов М.К., Розов Н.Х. Посо­бие по математике для поступающих в вузы (избранные вопросы элементарной математики). – М.: Наука, 1996.

6. Ерина Т.М. Задачи на движение. //Математика для школьников, № 3, 2005

7. Захарова А.Е. Диалог в ходе решения задач на движение //Математика в школе, №5,2003

8. Звавич Л.И. Задания для подготовки к письменному экзамену по математике в 11 классе: пособие для учителя – М.Просвещение, 2001

9. Колягин Ю.М. Задачи в обучении математике. Ч.1. Математические задачи как средство обучения и развития учащихся. – М.: Просвещение, 1977. – 108с.

10. Колягин Ю.М. Задачи в обучении математике. Ч.2. Обучение математике через задачи и обучение решению задач. – М.: Просвещение, 1977. – 142с.

11. Крупич В.И. Теоретические основы обучения решению школьных математических задач.– М.: Прометей, 1995. – 166с.

12. Кузнецова Л.В. Алгебра: сборник заданий для подготовки к итоговой аттестации в 9кл. / Л.В.Кузнецова и др. - М.: «Просвещение»,2007

13. Куланин Е.Д., Норин В.П., Федин С.Н., Шевченко Ю.А. 3000 конкурсных задач по математике. – М.: Айрис-пресс, 2003.

14. Лурье М.В., Александров Б.И. Задачи на составление уравнений. – М.: Наука, 1990.

15. Лысенко Ф.Ф. Математика. Подготовка к ЕГЭ – 2010(2011) / Ф.Ф.Лысенко, С.Ю.Кулабухова - Ростов – на – Дону.: « Легион – М», 2009

16. Программа общеобразовательных учреждений. «Алгебра 7 – 9 классы.» М.: «Просвещение» - 2008.

17. Прокофьев А., Соколова Т., Бардушкин В., Фадеичесва Т., Текстовые задачи. материалы вступительных экзаменов в МИЭТ. – Еженедедельная учебно-методическая газета «Математика», №9, 2005

18. Рудин В.И. Задачи на составление уравнений и арифметические задачи: пособме для учителей и школьников. – Томск, 1992

19. Фридман Л.М. Как научиться решать задачи: Беседы о решении мат. задач. Пособие для учащихся. – М.: Просвещение, 1986

20. Цыпкин А.Г., Цыпкин А.И. Справочник по методам решения задач по математике для средней школы. – М.: Наука, 1989.

21. Шевкин А.В. Сборник задач. 5-9 класс. – М.:Дрофа, 2006

22. Шестаков С.А. Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы: 9 кл. – М.: АСТ: Астрель, 2007

23. Эрдниев П.М. Преподавание математики в школе: Из опыта обучения методом укрупнения упражнений.– М.: Просвещение, 1978. – 304с.

24. Ященко И.В. Математика ЕГЭ Тематическая рабочая тетрадь / Э И.В.Ященко, С.А.Шестаков, П.И.Захаров – М.: «Экзамен», 2010

25. http://www.alleng.ru

26. http://ucheba.pro

27. http://festival.1september.ru

0 Звавич Л.И. Задания для подготовки к письменному экзамену по математике в 11 классе: пособие для учителя – М.Просвещение, 2001

0 Фридман Л.М. Как научиться решать задачи: Беседы о решении мат. задач. Пособие для учащихся. – М.: Просвещение, 1986

0 Крупич В.И. Теоретические основы обучения решению школьных математических задач.– М.: Прометей, 1995. – 166с

0 Крупич В.И. Теоретические основы обучения решению школьных математических задач.– М.: Прометей, 1995. – 166с

0 Звавич Л.И. Задания для подготовки к письменному экзамену по математике в 11 классе: пособие для учителя – М.Просвещение, 2001

0 Варшавский И.К., Гаиашвили М.Я., Глазков Ю.А. Текстовые задачи на Едином государственном экзамене. // Математика для школьников, №3, 2005

0 Высоцкий И.Р. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2010. Математика / И.Р.Высоцкий, Д.Д.Гущин и др. – М.: «АСТ Астрель»,2010

0 Ерина Т.М. Задачи на движение. //Математика для школьников, № 3, 2005

0 Каганов Э.Д. 400 самых интересных задач по школьному курсу – М.: ЮНВЕС., 1998

0 Каганов Э.Д. 400 самых интересных задач по школьному курсу – М.: ЮНВЕС., 1998