Получите свидетельство
Вход
Методическое пособие по предмету
«Математика»
Показательные уравнения и неравенства
(для практических занятий, с примерами решения).
Разработала: Латкина Н.А.
Простейшие показательные уравнения.
Пример 1. Решить уравнение
Решение. Приводим к одному основанию:
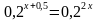
Если равны основания, то их степени также равны:
x+0,5=2x
x=0,5
Ответ: x=0,5
Задачи для самостоятельного решения.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 128*
20. 
21. 
22. 
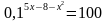
23. 
24. 
=1
25. 
Показательные уравнения, приводящиеся к линейному.
Пример 2. Решить уравнение
Решение. Перепишем уравнение в виде
Теперь в левой части уравнения вынесем за скобку общий множитель 
.
Получим ,
откуда 
x=1
Ответ: x=1
Задачи для самостоятельного решения.
1. 
2. 
3. 
4. 
5.
6. 
7.
8. 
9. 
10. 
11. 
12. 
13. 
14.
15.
16. 
17.
18. 
19. 
20. 
Показательные уравнения, приводящиеся к квадратному.
Пример 3. Решить уравнение
Решение. Перепишем уравнение в виде
Пусть 
, тогда уравнение примет вид
(посторонний корень)
Обратная замена: 
x=-2
Ответ: x=-2
Задачи для самостоятельного решения.
1. 
2. 
3. 
4.
5. 
6. 
7. 
8. 
9. 
10.
11.
12.
13.
14. 
15. 
16. 
17.
18. 
=0
19. 
20. 
21. 
=0
22. 
23. 
24. 
25. 
26.
27. 
Показательные неравенства.
Пример 4. Решить неравенство
Решение. Приводим к одному основанию:
Поскольку основание степени равняется 2 (больше единицы), то исходное неравенство равносильно неравенству
x3
Ответ: x3
Пример 5. Решить неравенство
Решение. Введем новую переменную 
причем t0. Исходное неравенство примет вид
Решением этого квадратичного неравенства является множество
Учитывая ограничение t0, получим 
откуда x0.
Ответ: x0
Задачи для самостоятельного решения.
1. 
2. 
3. 
4. 
5. 
6. 
7. ( 
8. 
9. 
10. 
11. 
12. 
13.
14. 
15. 
16.
17.
18. 
19.
20. (
21.
22.
23.
24.
25.
26. 
27.
28. 
29. 
30.
31. 
32. 
33. 
34. 
35. 
36. 
37.
38. 
39. 
40. 
41. 
42. 
43. 
44. 
45.(
46. 
47. 
48. 
49. 
50. 
51.(
52. 
53. 
54. 
55. 
56. 
57. 
58.
Методическое пособие по математике "Показательные уравнения и неравенства " (26.55 KB)
0
226
24
Нравится
0
