Экзаменационный материал по математике
по результатам освоения программы
среднего (полного) общего образования,
реализуемой в пределах основной
профессиональной образовательной
программы НПО
Комплект заданий
I вариант
Вычислите
25 1,5 + (0,25) -0,5 – 81 0,75 4 балла
Решите уравнение:
9 х = (1/27)2-х
Найти cos x, если sin x = - 15/17 π3π/2
4 балла
Найдите первообразную функции f(x) = x2 – 5, график которой проходит через точку (3;4) 4 балла
Изобразите график непрерывной функции, зная, что:
а) область определения функции есть промежуток [-6;1];
б) значения функции составляют промежуток [-2;4];
в) f ' (x) 0 для любого х из промежутков (-6;-4) и (-1;1), f ' (x) = 0 при х = - 4;
г) нули функции: х = - 4 и х = 0. 4 балла
Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 3х2 + 2х – 5 в его точке с абсциссой х = 2. 4 балла
Решите неравенство:
log ½ ( 2x – 1 ) -1 6 баллов
Вычислите:
( log 7 24 - 3 log 7 2) : (log 7 3 + log 7 9) 6 баллов
log 7 2) : (log 7 3 + log 7 9) 6 баллов
Решите уравнение:
(2х - 3)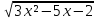 = 0 6 баллов
= 0 6 баллов
Решите систему уравнений
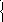 27 х = 9 у
27 х = 9 у
81 х = 3 у +1 8 баллов
II вариант
Вычислите
9 1,5 – 81 0,5 – (0,5) -2 4 балла
Решите уравнение:
27 1-х = 1/81 4 балла
Найти cos x, если sin x = 12/13 0π/2
4 балла
Найдите первообразную функции f(x) = 4 - x2, график которой проходит через точку (-3;10) 4 балла
Изобразите график непрерывной функции, зная, что:
а) область определения функции есть промежуток
[-5;2];
б) значения функции составляют промежуток [-2;5];
в) f '(x)
f '(x) 0 для любого х из промежутков (-5;-3) и (-1;2), f '(x) = 0 при х = -3;
г) нули функции: х = - 4 и х = -1. 4 балла
Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 2х3 – 3х2 - 4 в его точке с абсциссой х = -1. 4 балла
Решите неравенство:
log ⅓ ( 4x + 3 ) ≥ -1 6 баллов
Вычислите:
( 3 lg 2 + lg 0,25) : ( lg 14 - lg 7) 6 баллов
lg 2 + lg 0,25) : ( lg 14 - lg 7) 6 баллов
Решите уравнение:
(6х - 5)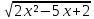 = 0 6 баллов
= 0 6 баллов
10.Решите систему уравнений
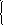 16 х = 64 у
16 х = 64 у
27 х +1 = 81 у -1 8 баллов
Эталоны ответов
Вычислите
25 1,5 + (0,25) -0,5 – 81 0,75
Решение:
25 1,5 + (0,25) -0,5 – 81 0,75 = (52) 1,5 + ((2)-2) -0,5 – (34)0,75 = 5 3 + 2 – 33 = 125 + 2 – 27 = 100
Решите уравнение: 9 х = (1/27) 2-х
Решение:
9 х = (1/27) 2-х
Используя свойства степеней, преобразуем правую и левую части уравнения к одному и тому же основанию
32х = (3-3) 2-х
32х = 3 3х-6
2х = 3х – 6
-х = - 6
х = 6
Ответ: х = 6
Найти cos x, если sin x = - 15/17 π
Решение:
х ϵ 3 четверти,
cos х
sin²α + cos²α=1
225/289 + cos2 х = 1
cos2 х = 64/289
cos х = - 8/17 , т.к. cos х
Ответ: cos х = - 8/17
Вычислите
9 1,5 – 81 0,5 – (0,5) -2
Решение:
9 1,5 – 81 0,5 – (0,5) -2 = (3 2) 1,5 - (34) 0,5 – (2-1) -2 = 3 3 - 3 2 – 22 = 27 - 9 - 4 = 14
Решите уравнение: 27 1-х = 1/81
Решение:
27 1-х = 1/81
Используя свойства степеней, преобразуем правую и левую части уравнения к одному и тому же основанию
(33) 1-х = 3 -4
3 3-3х = 3 -4
3-3х = - 4
-3х = - 7
х = 7/3
Ответ: х = 7/3
Найти cos x, если sin x = 12/13 0π/2 Решение:
х ϵ 1 четверти,
cos х 0
sin²α + cos²α=1
144/169 + cos²х =1
cos2 х = 25/169
cos х = 5/13 , т.к. cos х 0
Ответ: cos х = 5/13
Найдите первообразную функции f(x) = x2 – 5, график которой проходит через точку (3;4)
Решение:
f(x) = x2 – 5
F (x) = 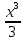 – 5х + С - первообразная функции
– 5х + С - первообразная функции
f(x) = x2 – 5 в общем виде
х = 3; F (x) = 4
4 = 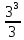 – 5˖3 + С
– 5˖3 + С
4 = 9 – 15 + С
С = 10
Изобразите график непрерывной функции, зная, что:
область определения функции есть промежуток [-6;1];
значения функции составляют промежуток [-2;4];
f '(x)
f '(x) 0 для любого х из промежутков (-6;-4) и (-1;1), f '(x) = 0 при х = - 4;
нули функции: х = - 4 и х = 0.
Решение:
D(x) ϵ [-6;1];
E(x) ϵ [-2;4];
f '(x) х ϵ (-4;-1),
f '(x) 0 х ϵ (-6;-4) ᴜ (-1;1),
f '(x) = 0 при х = - 4;
f (x) = 0 х = - 4 и х = 0.
Найдите первообразную функции f(x) = 4 – x2, график которой проходит через точку (-3;10)
Решение:
f(x) = 4 - x2
F (x) = 4х - 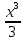 + С - первообразная функции
+ С - первообразная функции
f(x) = 4 – x2 в общем виде
х = - 3; F (x) = 10
10 = 4˖(-3) - 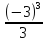 + С
+ С
10 = -12 + 9+ С
С = 13
Изобразите график непрерывной функции, зная, что:
область определения функции есть промежуток [-5;2];
значения функции составляют промежуток [-2;5];
f '(x)
f '(x) 0 для любого х из промежутков (-5;-3) и (-1;2),
f '(x) = 0 при х = -3;
нули функции: х = - 4 и х = -1.
Решение:
D(x) ϵ [-5;2];
E(x) ϵ [-2;5];
f '(x) х ϵ (-3;-1),
f '(x) 0 х ϵ (-5;-3) ᴜ (-1;2),
f '(x) = 0 при х = -3;
f (x) = 0 х = - 4 и х = -1.
Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 3х2 + 2х – 5 в его точке с абсциссой х = 2.
Решение:
k = f '(xо) k = f '(2)
f '(x) = 6х + 2
k = f '(2) = 14
Решите неравенство:
log ½ ( 2x – 1 ) -1
Решение:
log ½ ( 2x – 1 ) -1
ОДЗ: 2х – 10
2х - 1½)-1 т.к. логарифмическая функция log ½ ( 2x – 1 )- убывающая
2х – 10 2х - 1½)-1
х ½ х




х
½ 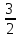
х ϵ ( ½;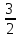 )
)
Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 2х3 – 3х2 – 4
в его точке с абсциссой х = -1.
Решение:
k = f '(xо) k = f '(-1)
f '(x) = 6х2 + 6х
k = f '(-1) = 0
Решите неравенство:
log ⅓ ( 4x + 3 ) ≥ -1
Решение:
log ⅓ ( 4x + 3 ) ≥ -1
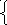
ОДЗ: 4х + 3 0
4x + 3 ≤ (⅓) -1 т.к. логарифмическая функция log ⅓ ( 4x + 3 ) - убывающая
4х + 3 0 4x + 3 ≤ (⅓) -1
х -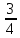 x ≤ 0
x ≤ 0




х

0
х ϵ ( ; 0]
Вычислите:
( log 7 24 - 3 log 7 2) : (log 7 3 + log 7 9)
log 7 2) : (log 7 3 + log 7 9)
Решение:
( log 7 24 - 3 log 7 2) : (log 7 3 + log 7 9) =
log 7 2) : (log 7 3 + log 7 9) =
( log 7 24 - log 7 23) : (log 7 3
 9) =
9) =
( log 7 24 - log 7 8) : (log 7 27) =
( log 7 3) : (log 7 3 3) = ( log 7 3) : 3  (log 7 3) = 1/3
(log 7 3) = 1/3
Решите уравнение:
(2х - 3)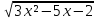 = 0
= 0
Решение:
(2х - 3)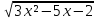 = 0
= 0
Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю.
2х - 3 = 0 или 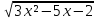 = 0
= 0
х = 3/2 Возведем обе части
уравнение в квадрат.
3х2 – 5х – 2 = 0
х1 = -1/3 х2 = 2
Ответ: х = -1/3; х = 3/2; х = 2.
Решите систему уравнений
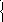 27 х = 9 у
27 х = 9 у
81 х = 3 у +1
Решение:
27 х = 9 у
х = 3 у +1
3 3х = 3 2у
3 4х = 3 у +1
Вычислите:
( 3 lg 2 + lg 0,25) : ( lg 14 - lg 7)
lg 2 + lg 0,25) : ( lg 14 - lg 7)
Решение:
( 3 lg 2 + lg 0,25) : ( lg 14 - lg 7) =
lg 2 + lg 0,25) : ( lg 14 - lg 7) =
(3 lg 2 + lg 2-2) : ( lg 2) = (3
lg 2 + lg 2-2) : ( lg 2) = (3 lg 2 - 2
lg 2 - 2 lg 2) : lg 2 =
lg 2) : lg 2 =
lg 2 : lg 2 = 1
Решите уравнение:
(6х - 5)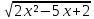 = 0
= 0
Решение:
(6х - 5)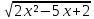 = 0
= 0
Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю.
6х - 5 = 0 или 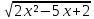 = 0
= 0
х = 5/6 Возведем обе части
уравнение в квадрат.
2х2 – 5х + 2 = 0
х1 = 1/2 х2 = 2
Ответ: х = 1/2; х = 5/6; х = 2.
Решите систему уравнений
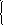
16 х = 64 у
27 х +1 = 81 у -1
Решение:
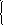
16 х = 64 у
27 х +1 = 81 у -1
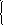
2 4х = 2 6у
3 3(х +1) = 3 4( у -1)
3х = 2у
4х = у +1
3х = 2у
у = 4х -1
3х = 2 (4х -1)
х = 0,4
у = 0,6
Ответ: (0,4; 0,6)
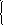
4х = 6у
3(х +1) = 4( у -1)
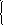
4х = 6у
3х + 3 = 4у - 4
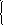
4х - 6у = 0 / 3
3
3х - 4у = - 7 / 4
4
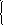
12х - 18у = 0
12х - 16у = -28
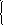
3х - 3у = 0
__
12х - 16у = -28
-2y = 28
y = - 14
4x – 6 ˖ (-14)= 0
4x + 84 = 0
x = - 21
Ответ: (-21; -14)
Экзамен по математике в образовательных учреждениях НПО сдается в письменной форме.
Результаты экзамена признаются удовлетворительными в случае, если обучающийся при сдаче экзамена по математике получил отметку не ниже удовлетворительной (три балла).
Результат экзамена по математике образовательными учреждениями НПО, признается как результат итогового контроля, влияет на занесение в диплом государственного образца о получении НПО записи о получении среднего (полного) общего образования.
На выполнение письменной экзаменационной работы по математике дается 5 астрономических часа.
Экзаменационная работа состоит из 2-х частей.
Обязательная часть содержит 6 заданий, дополнительная – 4. Выполнение каждого задания оценивается в баллах. За правильное выполнение одного задания обязательной части обучающийся получает 4 балла, за правильное выполнение одного задания дополнительной части – 6 баллов и за задание повышенной сложности 8 баллов..
Баллы, полученные за все выполненные задания, суммируются.
Оценка «отлично» ставится при выполнении в совокупности трех пунктов:
1.Изложено правильное понимание вопроса и дан исчерпывающий на него ответ, содержание раскрыто полно, профессионально, грамотно.
2.Письменная работа оформлена аккуратно, структурировано профессионально, грамотно, без произвольных сокращений и не содержит информации, не относящейся к предмету ответа.
3. Набрано 42 балла и более
Оценка «хорошо» ставится при выполнении в совокупности всех трех пунктов:
1. Изложено правильное понимание вопроса, дано достаточно подробное описание предмета ответа, приведены и раскрыты в тезисной форме основные понятия, относящиеся к предмету ответа, ошибочных положений нет.
2.Письменная работа содержит значительное число поправок, или отдельные нечеткие формулировки и информацию, не относящуюся к предмету ответа, или произвольные сокращения.
3. Набрано более 30 баллов
Оценка «удовлетворительно» ставится при выполнении в совокупности всех трех пунктов:
1.Изложено в целом правильное понимание вопроса. В то же время дано неполное, неточное описание предмета ответа и некоторых относящихся к нему понятий.
2.Письменная работа оформлена неаккуратно. Содержит исправления целыми или значительное количество нечетких формулировок.
3. Набрано более 24 баллов
Оценка «неудовлетворительно» ставится при выполнении любого из четырех пунктов:
2. Ответ претендента дан по указанному вопросу неверно, содержит, в основном, ошибочные положения.
3. В ответе не раскрыты основные понятия, относящиеся к вопросу.
4. Нарушение процедуры проведения экзамена, повлекшее за собой удаление с экзамена.
Набрано менее 24 баллов
| № задания | Проверяемые элементы содержания | Балл за задание |
| | Умение преобразовывать степенное выражение | 4 |
| | Умение решать показательное уравнение | 4 |
| | Умение применять основное тригонометрическое тождество и значения тригонометрических функций | 4 |
| | Умение находить первообразную функции | 4 |
| | Умение читать свойства функции, применять производную к исследованию функции и строить график в координатной плоскости по свойствам функции | 4 |
| | Умение находить угловой коэффициент касательной к графику функции | 4 |
| | Умение решать логарифмическое неравенство | 6 |
| | Умение преобразовывать логарифмическое выражение | 6 |
| | Умение решать комбинированное линейно-рациональное уравнение | 6 |
| | Умение решать систему показательных уравнений | 8 |
| баллы | Критерии оценки выполнения задания № 1-6 |
| 4 | Приведена верная последовательность всех шагов решения: все преобразования и вычисления выполнены, верно. Получен верный ответ. |
| 2 | Приведена верная последовательность всех шагов решения, но допущена одна описка и/или вычислительная ошибка, не влияющая на дальнейший ход решения. В результате этой описки или ошибки может быть получен неверный ответ. |
| 0 | Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 2 и 4 баллов. |
| баллы | Критерии оценки выполнения задания № 7-9 |
| 6 | Приведена верная последовательность всех шагов решения: все преобразования и вычисления выполнены, верно. Получен верный ответ. |
| 4 | Приведена верная последовательность всех шагов решения, но допущена одна описка и/или вычислительная ошибка, не влияющая на дальнейший ход решения. В результате этой описки или ошибки может быть получен неверный ответ. |
| 2 | Верно выполнена только часть решения, а остальные шаги или отсутствуют, или сделаны с ошибкой. |
| 0 | Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 2 и 4 баллов. |

 Получите свидетельство
Получите свидетельство Вход
Вход












 Методическая разработка "Промежуточная аттестация по математике" (114.47 KB)
Методическая разработка "Промежуточная аттестация по математике" (114.47 KB)
 0
0 212
212 5
5 Нравится
0
Нравится
0


