Метод неопределенных коэффициентов

Метод неопределенных коэффициентов

Дьёрдь Пойа (1887-1985)

Трудность решения в какой-то мере входит в само понятие задачи: там, где нет трудности, нет и задачи.

Цель : исследовать возможность применения метода неопределенных коэффициентов при решении задач элементарной математики и при решении функциональных уравнений.

Задачи :

• Изучить литературу .

2. Доказать теоремы Виета, Безу, схему Горнера, с помощью метода неопределенных коэффициентов.

3. Рассмотреть возможность использования метода в различных задачах алгебры.

4. Изучить решение функциональных уравнений.

5.Ознакомить учащихся 10-х классов с методом неопределенных коэффициентов.

Методом неопределенных коэффициентов называют метод, применяемый для отыскания коэффициентов выражений, вид которых заранее известен.

0, х 2 - 1 ≤ 0, т.е - 1 ≤ х ≤ 1. Ответ: [ - 1 ; 1 ] . " width="640"

х 4 - х 3 + х – 1 ≤ 0

Решение: х 4 - х 3 + х – 1 = (х 2 - 1)(х 2 + рх + q )

х 4 - х 3 + х – 1 = х 4 + рх 3 + х 2 q – х 2 – рх – q

х 4 1 = 1

х 3 р = - 1

х 2 q – 1 = 0 р = - 1, q = 1

х 1 - р = 1

х 0 - q = - 1

(х 2 - 1)( х 2 - х + 1) ≤ 0

х 2 - х + 10,

х 2 - 1 ≤ 0, т.е - 1 ≤ х ≤ 1.

Ответ: [ - 1 ; 1 ] .

Теоремы, доказанные методом неопределенных коэффициентов:

• Теорема Виета для уравнений 3 и 4 степеней
• Теорема Безу
• Схема Горнера

Использование метода:

• Расположение многочлена по степеням.
• Представление произведения в виде многочлена стандартного вида.
• Разложение многочлена на множители.
• Разложение дроби на суммы простых дробей.
• Избавление иррациональности в знаменателе.
• Решение уравнений и неравенств высших степеней.
• Решение функциональных уравнений

Найти все значения а , при которых уравнение 2х 3 -4х 2 –8х +а = 0 имеет два различных корня

2 х 3 - 4х 2 – 8х + а = 2(х - А) 2 (х - В)

2х 3 -4х 2 –8х +а = 2х 3 +х 2 (-2В –4А) +х(4ВА + 2А 2 ) –2А 2 В

х 3 2 = 2

х 2 - 2В – 4А = - 4

х 1 4ВА + 2А 2 = -8

х 0 – 2А 2 В = а

А 1 = - , В 1 = , А 2 = 2, В 2 = - 2.

Ответ: а 1 = , а 2 = 16

2х 3 -4х 2 –8х +а = 0

у = -а

у = 2х 3 -4х 2 –8х D (у)= R

у = 6х 2 -8х–8

у

min

max

х

у

-2/3

2

х

у

-24,5

0

0

2

-16

-15

3

-6

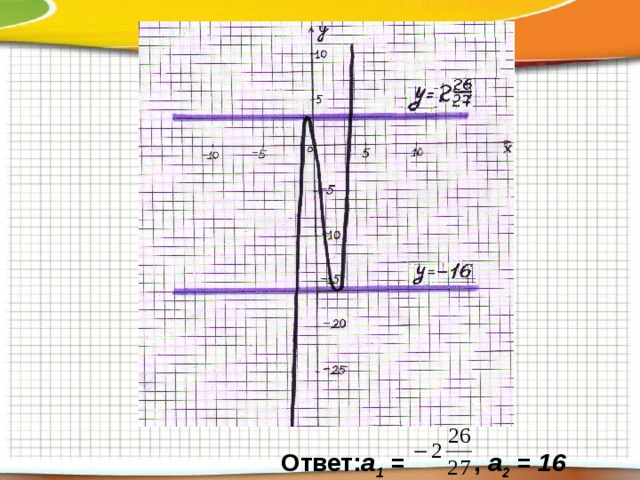
Ответ: а 1 = , а 2 = 16

Решение:

( А+В+С) к 2 +(А - С) к – В = 1

к 2 А+В+С = 0

к 1 А – С = 0

к 0 - В = 1

А= , В = - 1, С = .

(2)

(1)

Ответ:

Избавится от иррациональности в знаменателе дроби

Решение: А + В√2 + С√3 + D √6

А + В + С + D =

(А – 2В + 3С) + ( - А +В+ 3 D ) + (А + С+ 2 D ) + (В – С + D ) = 1+ -

А -2В + 3С = 1,

- А+ В + 3 D = 1,

А + С – 2 D = - 1,

В - С + D = 0

Откуда А = 0, В = - 1\2, С = 0, D = 1\2,

=

Функция у = ƒ(х) при всех х определена, непрерывна и удовлетворяет условию ƒ(ƒ(х)) = ƒ(х) + х. Найти 2 такие функции.

Решение: ƒ(ƒ(х)) – ƒ(х) = х

ƒ(х) = ах + b

(а 2 - а) х + а b = х

а 2 – а = 1

а b = 0

а = 0,5 (1 ) , b = 0.

ƒ(х) = 0,5(1 )х

Ответ: ƒ(х) = 0,5 (1 )х.

Алексей Николаевич Крылов

(1863-1945)

  "Рано или поздно всякая правильная математическая идея находит применение в том или ином деле"