Секция: Математика
Тема: «Медианы треугольника»
Место выполнения работы:
МБОУ ордена «Знак Почёта»
им. А. В. Луначарского
гимназия №5, г. Владикавказ, РСО - А
Автор - Кобаидзе Нина Ивановна, учитель математики
План
I. Вступление
II. Основная часть. Медианы треугольника.
III. Геометрический практикум.
IV. Использованная литература
Цель: изучить свойства медиан треугольника.
Объект исследования: медианы треугольника.
Предмет исследования: свойство медианы треугольника.
Задачи: Собрать материал из источников, где используется рассматриваемое свойство медиан треугольника.
Показать разнообразие исследуемого материала.
Решить задачи с использованием свойств медиан треугольника
Задачи по геометрическому практикуму: Решить задачи с применением свойств медиан треугольника (из ГИА и ЕГЭ).
Актуальность:
Человеческая память несовершенна, уходящее время уносит с собой и в себе то, что изучается сегодня вскользь, а не глубинно, в данном случае: свойство медиан треугольника. Сегодня выпускники сдают ГИА, ЕГЭ или компьютерное тестирование, участвуют в олимпиадах, где часто встречаются задачи с применением свойства медиан треугольника. Поэтому нам захотелось напомнить всем школьникам и будущим абитуриентам о великом свойстве медиан треугольника.
I. Вступление:
Доказательство называется строгим,
если таковым его считает
большинство математиков.
Морис Клайн.
Мы выбрали эту тему, чтобы как следует изучить свойство медиан треугольника, помнить его и применять его при решении задач.
Мы собрали, по возможности, различные способы решения задач. Решение одной и той же задачи различными методами дает возможность полнее исследовать свойства геометрической фигуры и выявить наиболее простое решение. Нередко найденный способ решения может быть в дальнейшем использован в ГИА и ЕГЭ для решения более трудных задач.
Методы исследования:
1) теоретические, (т.е. изучение источников информации: книг и журнальных статей в печатном и электронном видах);
2) практические, (т.е. уроки, консультации, семинары, коллоквиумы и факультативы в школе, олимпиады и тестирование).
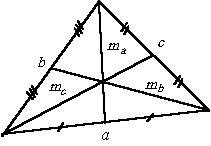
Медианы треугольника
Как известно, медианами треугольника называются отрезки, соединяющие его вершины с серединами противоположных сторон. Все три медианы пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины. 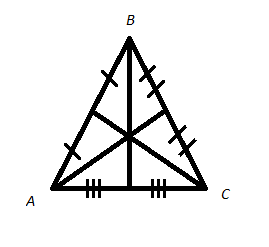
Точка пересечения медиан является также центром тяжести треугольника.
Если подвесить картонный треугольник в точке пересечения его медиан, то будет находиться в состоянии равновесия.
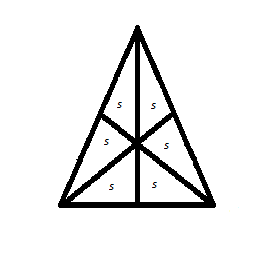
Любопытно, что все шесть треугольников, на который всякий треугольник разбивается своими медианами, имеют одинаковые площади.
Медианы треугольника через его стороны выражаются так:
ma = 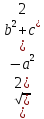 mb =
mb = 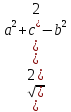
mс = 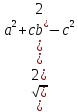
1. Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны, т. е. если ma 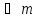 b , то
b , то 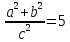
2. Построим треугольник, стороны которого равны медианам данного треугольника, когда медианы построенного треугольника будут равны ¾ сторон первоначального треугольника.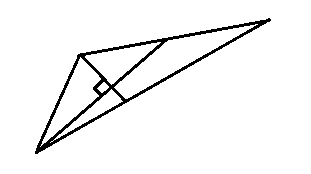
Данный треугольник назовем первым, треугольник из его медиан – вторым, треугольник из медиан второго - третьим и т. д. Тогда с нечетными номерами (1,3,5,7…)
Подобны между собой и треугольники с четными номерами(2,4,6,8…) также подобны между собой. Сумма квадратов длин всех медиан треугольника равняется ¾ сумма квадратов длин его сторон.
Знаменитый немецкий математик Г. Лейбниц обнаружил замечательный факт: сумма квадратов расстояний от произвольной точки плоскости до вершин треугольника, лежащего в этой плоскости, равняется сумме квадратов расстояний от точки пересечения медиан до его вершин, сложенной с утроенным квадратом расстояния от точки пересечения медиан до выбранной точки.
Из этой теоремы следует, что точка на плоскости, для которой сумма квадратов расстояний до вершин данного треугольника является минимальной - это точка пересечения медиан этого треугольника.
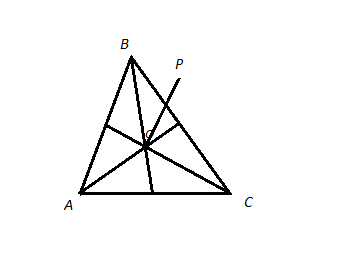 В то же время минимальная сумма расстояния до вершин треугольника (а не их квадратов) будет для точки, из которой каждая сторона видна под углом в 120 ̊, если ни один из углов треугольника не больше 120 ̊ (точка Ферма), и для вершины тупого угла, если он …
В то же время минимальная сумма расстояния до вершин треугольника (а не их квадратов) будет для точки, из которой каждая сторона видна под углом в 120 ̊, если ни один из углов треугольника не больше 120 ̊ (точка Ферма), и для вершины тупого угла, если он …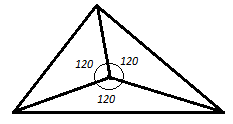
По теореме Лейбница и предыдущего утверждения легко найти расстояние d от точки
пересечения медиан до центра описанной окружности. Действительно, это расстояние по теореме Лейбница равно корню квадратному из одной трети разности между суммой квадратов расстояний от центра описанной окружности до вершин треугольника и суммой квадратов расстояний от точки пересечения медиан до вершин треугольника.
Получаем:
d=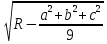
На уроках геометрии можно решить следующие задачи на построение: постройте с помощью циркуля и линейки треугольник -
По двум сторонам и медиане, опущенной на третью сторону;
по двум сторонам и медиане, опущенной на одну из них.
По трем медианам
Нетрудно совершить построение с помощью циркуля и линейки в аналогичных задачах, полученных из этих с заменой слова “медиана ” словом “высота”, но при замене слова “медиана ” - словом “биссектриса”, указанное построение в ряде случаев произвести, оказывается, невозможно.
Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противоположной стороны.
Медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и делятся этой точкой в отношении 2/1, считая от вершины.
Медиана делит треугольник на два равновеликих треугольника. Три медианы делят треугольник на шесть равновеликих треугольников.
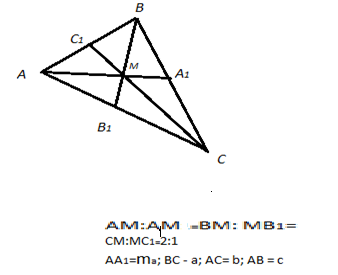
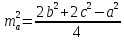
В любом треугольнике можно провести 3 медианы. Все они
пересекаются в одной точке, в центре (центре тяжести) треугольника. 
AK = KC ,
BK — медиана ![]() ABC ,
ABC ,
О — центр ![]() A 1B 1C 1 .
A 1B 1C 1 .
Задачи:
№1
Стороны треугольника равны 8, 9 и 13 см. К наибольшей стороне треугольника проведена медиана. Определите медиану треугольника исходя из размеров его сторон.
Решение.
Задача имеет два способа решения. Первый, который является наиболее универсальным.
Способ 1.
Применим Теорему Стюарта, согласно которой квадрат медианы равен одной четвертой от суммы удвоенных квадратов сторон, из которой вычли квадрат стороны, к которой проведена медиана.
mc2 = (2a2 + 2b2 - c2 ) / 4 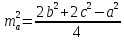
Соответственно
mc2 = ( 2 * 82 + 2 * 92 - 132) / 4
mc2 = 30,25
mc = 5,5 см
Способ 2.
Второй способ решения - это дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.
Продлим стороны треугольника и медиану, достроив их до параллелограмма. В этом случае медиана треугольника будет равна половине диагонали получившегося параллелограмма, а две стороны треугольника - его боковым сторонам. Третья сторона треугольника, к которой была проведена медиана, является второй диагональю получившегося параллелограмма.
Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
2(a2+b2)=d12+d22
Обозначим диагональ параллелограмма, которая образована продолжением медианы исходного треугольника как х, получим:
2( 82 + 92 ) = 132 + x2
290 = 169 + x2
x2 = 290 - 169
x2 = 121
х = 11. Поскольку искомая медиана равна половине диагонали параллелограмма, то величина медианы треугольника составит 11 / 2 = 5,5 см
Ответ: 5,5 см
№2
В выпуклом четырехугольнике ABCD расстояние между точками пересечения медиан треугольников ABD и BCD равно a. Определить AC.
Решение
|
| Пусть M и N – точки пересечения медиан в треугольниках ABD и BCD соответственно и K – середина отрезка BD. Тогда |
Ответ: 3a.
Для нахождения медианы треугольника по трем его сторонам удобно использовать рассуждения при решении типовой задачи.
| | |
№3
Определить стороны треугольника, если его медианы равны
и
.
Решение
Полагая в предыдущих трех равенствах ,
и
, после возведения обеих частей в квадрат получим:
Решая систему линейных уравнений, найдем x = 16, y = 36 и z = 64, а значит, стороны треугольника равны 4; 6 и 8.
Ответ: 4; 6 и 8 .
При решении задач, в которых упоминается медиана треугольника, часто достраивают треугольник до параллелограмма так, чтобы медиана была половиной диагонали.
|
| Так как в параллелограмме сумма квадратов всех его сторон равна сумме квадратов диагоналей, то |
№4. Длина медианы BK остроугольного треугольника ABC равна 8 см. Длины ортогональных проекций этой медианы на стороны AB и BC равны 6 см и см соответственно. Найти длину стороны AC.
Решение
Пусть AK = BK = x (см. рисунок).
По теореме Пифагора имеем
и ,
а значит и
.
|
| Так как сумма квадратов диагоналей параллелограмма ABCD равна сумме квадратов всех его сторон, то получаем уравнение Для удобства, полагая |
После преобразований получаем , и поэтому t = 1.
Откуда находим и
.
Поэтому (см).
Ответ: см.
Медиана
Медианой треугольника называется отрезок,
который соединяет вершину треугольника с серединой
противолежащей стороны.
Медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и делятся этой точкой в отношении 2 : 1, считая от вершины.
Медиана делит треугольник на два равновеликих треугольника. Три медианы делят треугольник на шесть равновеликих треугольников.
Литература:
1. Учебник 7-9 класс геометрии. Авторы: Л.С. Атанасян, В.Ф.Бутузов, С.Б. Кадамцев, Э.Г. Позняк, И.И. Юдина.
2. Квант №7 1990 г., Калейдоскоп “Кванта”, стр. 40, 41
3. Банк заданий ФИПИ
2

 Получите свидетельство
Получите свидетельство Вход
Вход











 «Медианы треугольника» (190.66 KB)
«Медианы треугольника» (190.66 KB)
 0
0 2137
2137 61
61 Нравится
0
Нравится
0


