Аннотация
Урок является последним уроком по теме «Треугольники». На следующем уроке планируется проведение контрольной работы, проверка усвоения материала по данной теме. В теме «Треугольники» изучаются:
- Признаки равенства треугольников;
- Внешний угол треугольника;
- Сумма углов треугольника.
- Свойства биссектрисы, высоты и медианы равнобедренного треугольника.
Тема «Треугольники» является одной из самых важных в курсе планиметрии. Планирование и проведение урока нацелено на формирование представления учащихся о сущности теорем, умения применять их к решению задач, а также на развитие правильной математической речи учащихся. Учащиеся знакомятся с основными понятиями, записывают решения задач в тетрадь. На уроке сочетаются устные и письменные формы работы, беседа, рассказ учителя, работа с учебником, работа у доски и в тетради, самостоятельные работы.
Результатом деятельности учащихся на данном уроке должно стать составление кластера по данной теме, также выработка умения решать простейшие задачи с применением признаков равенства треугольников, нахождения неизвестных углов. Составление кластера, решение задач развивает логическое мышление, внимание и творческие способности.
Цель урока:
формирование у учащихся умения применять полученные знания в нестандартных ситуациях, подготовка к итоговой аттестации.
Для успешного выполнения экзаменационных заданий необходимы твердые знания основных геометрических фигур и некоторый практический опыт. Работа может быть полезна учащимся не только 9 класса, но и 8 и 10 классов, которые в будущем будут сдавать ЕГЭ.
В содержании урока есть историческая справка о треугольниках и краткий справочный материал.
Задачи урока:
Обучающие:
предоставить условия учащимся для самостоятельного приобретения знаний о треугольниках;
сформировать умение применять данные знания при решении геометрических задач.
Развивающие:
развивать воображение, логическое мышление учащихся посредством использования творческих заданий;
продолжить работу над развитием умения сравнивать, обобщать, выделять главное, существенное;
продолжить работу над развитием памяти, внимания, словарного запаса учащихся;
Воспитательные:
продолжить работу над формированием научного мировоззрения, интереса к процессу познания;
формировать ответственное отношение к учебному труду;
воспитывать умение работать творчески, слушать учителя, товарищей, себя.
Ход урока
1. Организационный момент.
Приветствие учащихся учителем, организация внимания учащихся.
2. Актуализация знаний учащихся по изучаемой теме.
- С какими геометрическими понятиями ассоциируется слово «ТРЕУГОЛЬНИК»?
- Постройте произвольный треугольник. Обозначьте его.
1. Что называется треугольником;
2. Запишите в тетради и на доске все элементы, которые только что перечислили.
Учащиеся называют элементы треугольника.
Выполняют чертежи и записи в тетрадях и на доске математическим языком/
2. На доске изображены треугольники: (приложение №1).
- Сгруппируйте все треугольники по видам.
- Дайте определение каждому виду треугольников
Учащиеся группируют треугольники по сторонам и углам (работа парами)
3. Среди основных элементов треугольника, кроме вершин, сторон и углов, выделяют медиану, биссектрису и высоту.
- В треугольнике АВС постройте медиану из вершины А. Дайте определение медианы.
- Дайте определение биссектрисы треугольника и постройте ее из вершины В.
Следующий элемент треугольника – это высота.
- Дайте определение высоты треугольника и постройте ее из вершины С.
Определение: Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В ∆АВС учащиеся строят медиану. (приложение 3, рис №1)
Определение: Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противополож-ной стороны (приложение 3, рис №2).
Определение: Высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противопо-ложную сторону (приложение 3, рис №3).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход







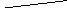 ис.1 Рис. 2 Рис.3 Рис.4
ис.1 Рис. 2 Рис.3 Рис.4 
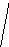


 ис.5 Рис.6 Рис.7
ис.5 Рис.6 Рис.7 
 азносторонний: рис.5
азносторонний: рис.5 строугольный: рис. 1,4,5,
строугольный: рис. 1,4,5, авнобедренный: рис.4
авнобедренный: рис.4 рямоугольный: рис. 2,6,7.
рямоугольный: рис. 2,6,7. авносторонний: рис. 1
авносторонний: рис. 1
 упоугольный: рис. 3.
упоугольный: рис. 3.

 высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону (рис. 3) CK - высота.
высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону (рис. 3) CK - высота. 










 Конспект урока по математике "Треугольники" (0.13 MB)
Конспект урока по математике "Треугольники" (0.13 MB)
 0
0 761
761 55
55 Нравится
0
Нравится
0








