Материал по математике "Уравнения с параметром"

Задания.

1. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние.

x⁴+(a-3)_²=│x-a+3│+│x+a-3│

2. Най­ди­те все зна­че­ния па­ра­мет­ра a, при ко­то­рых урав­не­ние

(x+1/x-a)²-(a+9)(x+1/x-a)+2a(9-a)=0

имеет ровно 4 ре­ше­ния.

3. Опре­де­ли­те, при каких зна­че­ни­ях па­ра­мет­ра a урав­не­ние

│x-2│=alog₂│x-2│

имеет ровно два ре­ше­ния.

4. Найти все зна­че­ния a, при каж­дом из ко­то­рых функ­ция

f(x)=x²-2│x-a²│-4x

имеет хотя бы одну точку мак­си­му­ма.

5. Най­ди­те все зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых урав­не­ние

│x-a2+a+2│+│x-a²+3a-1│=2a-3

имеет корни, но ни один из них не при­над­ле­жит ин­тер­ва­лу (4; 19).

6. Най­ди­те все зна­че­ние a, при каж­дом из ко­то­рых гра­фик функ­ции

f(x)=x²-3x+2-│x²-5x+4│-a

пе­ре­се­ка­ет ось абс­цисс менее чем в трех раз­лич­ных точ­ках.

7. Най­ди­те все зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых урав­не­ние

│x-a²+4a-2│+│x-a²+2a+3│=2a-5

имеет хотя бы один ко­рень на от­рез­ке [5; 23].

Весь материал - в документе.

Уравнения с параметром

1. Най­ди­те все зна­че­ния 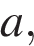при каж­дом из ко­то­рых урав­не­ние 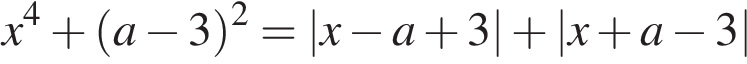либо имеет един­ствен­ное ре­ше­ние, либо не имеет ре­ше­ний.

2. Най­ди­те все зна­че­ния па­ра­мет­ра a, при ко­то­рых урав­не­ние

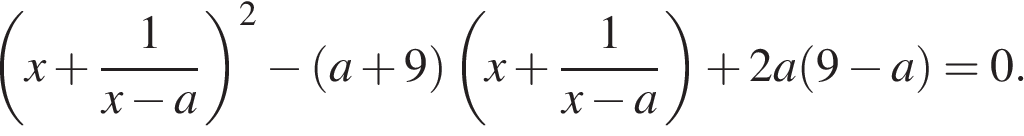
имеет ровно 4 ре­ше­ния.

3. Опре­де­ли­те, при каких зна­че­ни­ях па­ра­мет­ра 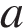урав­не­ние

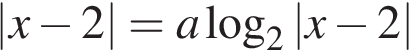
имеет ровно два ре­ше­ния.

4. Найти все зна­че­ния a, при каж­дом из ко­то­рых функ­ция

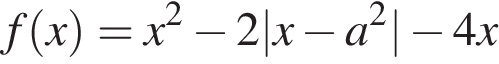
имеет хотя бы одну точку мак­си­му­ма.

5. Най­ди­те все зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых урав­не­ние

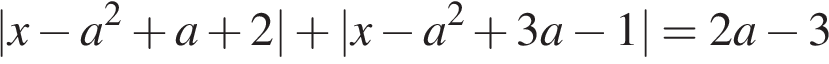
имеет корни, но ни один из них не при­над­ле­жит ин­тер­ва­лу (4; 19).

6. Най­ди­те все зна­че­ние a, при каж­дом из ко­то­рых гра­фик функ­ции

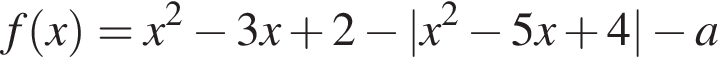
пе­ре­се­ка­ет ось абс­цисс менее чем в трех раз­лич­ных точ­ках.

7. Най­ди­те все зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых урав­не­ние

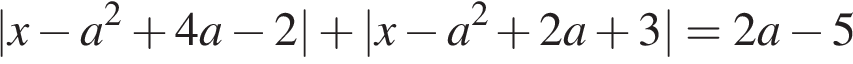
имеет хотя бы один ко­рень на от­рез­ке [5; 23].

8. Най­ди­те все зна­че­ния па­ра­мет­ра при каж­дом из ко­то­рых не­ра­вен­ство 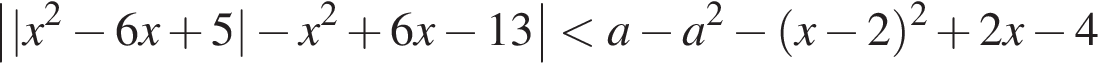имеет един­ствен­ное целое ре­ше­ние.

9. Най­ди­те все зна­че­ния при каж­дом из ко­то­рых наи­мень­шее зна­че­ние функ­ции 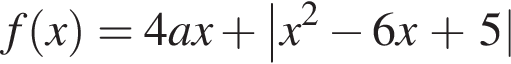боль­ше, чем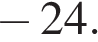

10. Най­ди­те все зна­че­ния 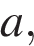при каж­дом из ко­то­рых гра­фик функ­ции 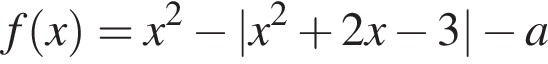пе­ре­се­ка­ет ось абс­цисс более чем в двух раз­лич­ных точ­ках.

11. Найти все зна­че­ния па­ра­мет­ра 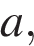при каж­дом из ко­то­рых среди зна­че­ний функ­ции 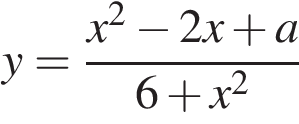есть ровно одно целое число.

12. Най­ди­те все зна­че­ния па­ра­мет­ра а, при каж­дом из ко­то­рых мно­же­ство зна­че­ний функ­ции 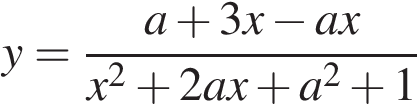со­дер­жит от­ре­зок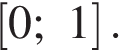

13. Най­ди­те все такие зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых урав­не­ние 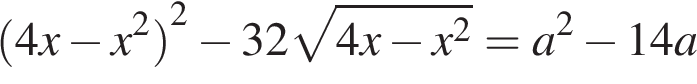имеет хотя бы одно ре­ше­ние.

14. Най­ди­те все такие зна­че­ния па­ра­мет­ра a, при каж­дом из ко­то­рых урав­не­ние 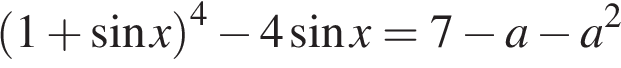не имеет ре­ше­ний.

15. Най­ди­те все зна­че­ния 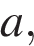при каж­дом из ко­то­рых си­сте­ма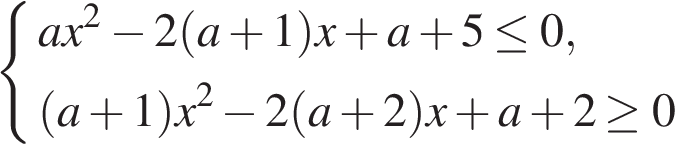

имеет един­ствен­ное ре­ше­ние.

16. Най­ди­те все такие зна­че­ния па­ра­мет­ра 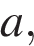при каж­дом из ко­то­рых урав­не­ние 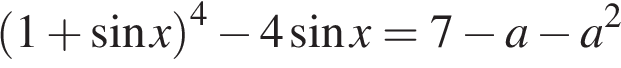не имеет ре­ше­ний.

17. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых си­сте­ма

имеет един­ствен­ное ре­ше­ние.

18. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых си­сте­ма

имеет един­ствен­ное ре­ше­ние.

19. Най­ди­те все по­ло­жи­тель­ные зна­че­ния a , при каж­дом из ко­то­рых си­сте­ма

имеет един­ствен­ное ре­ше­ние.

20. Най­ди­те все зна­че­ния па­ра­мет­ра a, при ко­то­рых любое число из от­рез­ка 2 ≤ x ≤ 3 яв­ля­ет­ся ре­ше­ни­ем урав­не­ния

21. Най­ди­те все зна­че­ния 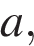при каж­дом из ко­то­рых урав­не­ние либо имеет един­ствен­ное ре­ше­ние, либо не имеет ре­ше­ний.

22. Най­ди­те все зна­че­ния а. при каж­дом из ко­то­рых урав­не­ние

на про­ме­жут­ке имеет более двух кор­ней.

23. Най­ди­те все зна­че­ния 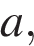при каж­дом из ко­то­рых урав­не­ние

на про­ме­жут­ке имеет боль­ше двух кор­ней.

24. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

имеет един­ствен­ный ко­рень.

25. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых урав­не­ние

имеет един­ствен­ный ко­рень.

26. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых наи­мень­шее зна­че­ние функ­ции боль­ше 1.

27. Най­ди­те все зна­че­ния 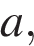при каж­дом из ко­то­рых урав­не­ние

имеет хотя бы одно ре­ше­ние.

28. Най­ди­те все зна­че­ния 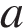, при каж­дом из ко­то­рых урав­не­ние

имеет хотя бы одно ре­ше­ние.

29. Най­ди­те все зна­че­ния па­ра­мет­ра a, при ко­то­рых урав­не­ние не имеет ре­ше­ний.

30. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых урав­не­ние

имеет един­ствен­ный ко­рень.

31. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние имеет хотя бы один ко­рень.

32. Най­ди­те все зна­че­ния 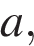при ко­то­рых урав­не­ние имеет на про­ме­жут­ке един­ствен­ный ко­рень.

33. Най­ди­те все зна­че­ния a, при ко­то­рых урав­не­ние имеет хотя бы один ко­рень, при­над­ле­жа­щий про­ме­жут­ку (−1; 1].

34. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

имеет един­ствен­ный ко­рень.

35. Най­ди­те все зна­че­ния па­ра­мет­ра 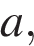при каж­дом из ко­то­рых урав­не­ние

имеет един­ствен­ное ре­ше­ние. Най­ди­те это ре­ше­ние для каж­до­го зна­че­ния a.

36. Най­ди­те все зна­че­ния 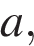при ко­то­рых не­ра­вен­ство вы­пол­ня­ет­ся для всех дей­стви­тель­ных зна­че­ний

37. Най­ди­те все зна­че­ния a, при ко­то­рых любое ре­ше­ние урав­не­ния

при­над­ле­жит от­рез­ку

38. Най­ди­те все зна­че­ния па­ра­мет­ра 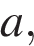при ко­то­рых урав­не­ние

имеет ровно два ре­ше­ния.

39. Най­ди­те все зна­че­ния 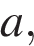при каж­дом из ко­то­рых урав­не­ние имеет более двух кор­ней.

40. Най­ди­те все зна­че­ния 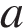, при ко­то­рых урав­не­ние на про­ме­жут­ке имеет ровно два корня.

41. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

имеет хотя бы один ко­рень.

42. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых урав­не­ние имеет ровно три раз­лич­ных ре­ше­ния.

43. Най­ди­те все зна­че­ния 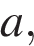при ко­то­рых урав­не­ние

имеет хотя бы одно ре­ше­ние.

44. При каких 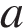урав­не­ние имеет ровно три корня?

45. Най­ди­те все зна­че­ния a, при ко­то­рых урав­не­ние

имеет ровно два ре­ше­ния.