Напомним свойства числовых неравенств.
1. Если а > b, то b < а; наоборот, если а < b, то b > а.
2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c).
Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину.
4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.
Замечание.
Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое.

6. Если а > b и m – положительное число, то m а > m b и, т.е. обе части неравенства можно умножить или разделить на одно и то же положительное число (знак неравенства остаётся тем же).
Если же а > b и n – отрицательное число, то n а < n b и, т.е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при этом знак неравенства нужно переменить на противоположный.
7. Если а > b и c > d, где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


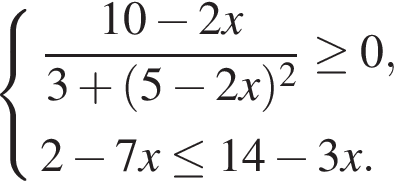
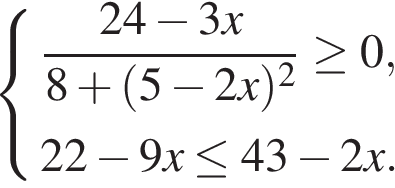









 Материал по математике "Системы неравенств" (46.21 КB)
Материал по математике "Системы неравенств" (46.21 КB)
 0
0 436
436 48
48 Нравится
0
Нравится
0



