Теорема
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношение 2:1, считая вершины
Доказательство
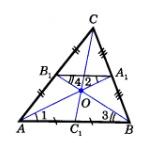
Рассмотрим произвольный треугольник ABC. Обозначим буквой O точку пересечения его медиан AA1 и BB1 и проведем среднюю линию A1B1 этого треугольника
Отрезок A1B1 параллелен стороне AB, поэтому углы 1 и 2, а также углы 3 и 4 равны как накрест лежащие углы при пересечении параллельных прямых AB и A1B1 секущими AA1 и BB1. Следовательно, треугольники AOB и A1OB1 подобны по двум углам, и, значит их стороны пропорциональны:
AOA1O=BOB1O=ABA1B1

Но AB=2⋅A1B1, поэтому AO=2⋅A1O и BO=2⋅B1O. Таким образом, точка O пересечения медиан AA1 и BB1 делит каждую из них в отношении 2:1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан BB1 и CC1 делит каждую из них в отношении 2:1 считая от вершины, и, следовательно, совпадает с точкой O.
Итак, все три медианы треугольника ABC пересекаются в точке O и делятся ею в отношении 2:1, считая от вершины
Теорема доказана.
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Материал по математике по теме «Медианы» (20.08 КB)
Материал по математике по теме «Медианы» (20.08 КB)
 0
0 687
687 5
5 Нравится
0
Нравится
0



