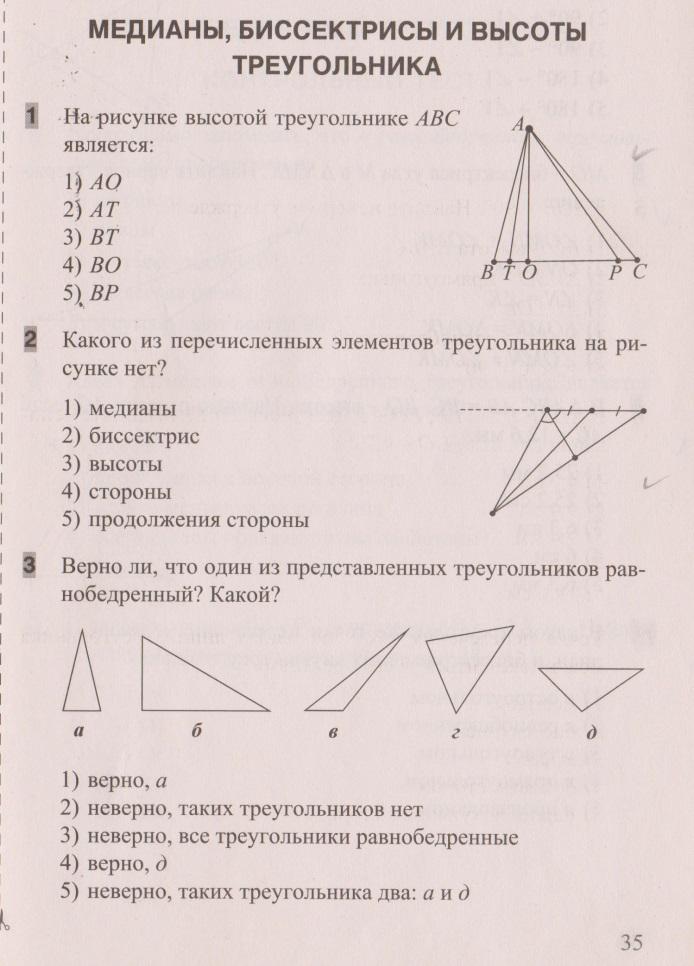
Бинарный урок по математике и информатике в 7 классе
Тема: Медиана, биссектриса и высоты треугольника
Цель: повторить понятия высоты, медианы и биссектрисы треугольника, учиться выполнять их построение.
Задачи:
формировать понятия высоты, медианы и биссектрисы треугольника.
Способствовать развитию устойчивого познавательного интереса к изучению геометрии.
Развивать логическое мышление учащихся.
Научиться практически применять полученные знания с ипользованием программных средств
Тип урока: урок обобщения изученного материала.
Формы организации учебной деятельности: коллективная, индивидуальная, групповая
Оборудование и наглядность урока:
Программа «Живая математика»;
Опорные конспекты по теме «Медиана, биссектриса и высота треугольника»;
компьютер с мультимедийным проектором;
тесты.
Ход урока
Организационный момент.
Сообщение темы урока и постановка задач урока
Беседа с учителем:
Вопросы:
1.Посмотрите, пожалуйста, какая геометрическая фигура у меня в руках? (Треугольник)
2.А что называется треугольником?
(Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).
Сколько у него элементов? (6)
Назовите элементы треугольника. (Три стороны и три угла).
Какие виды треугольника вы знаете? (прямоугольный, равнобедренный, равносторонний)
3. Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? Где он находится?
4. А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного. Вот сегодня мы и поговорим о этой геометрической фигуре. А вернее о элементах треугольника таких как медиана, биссектриса и высота.
Выполним задание№1
Определим цели урока.
Т.О. ребята, давайте определим цель нашего урока. (Сегодня мы должны повторить что такое медиана, биссектриса и высота треугольника). А основной задачей урока будет научится строить эти элементы треугольника линейкой, а еще с помощью программы «Живая математика. В этом вам поможет Солдатова Д.Х.
III.Актуализация знаний. Повторение основных понятий.
Практическое задание построение медианы, биссектрисы и высоты треугольника.
Опорный конспект для 1 группы:
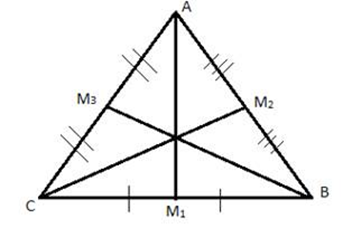
1.Начертите треугольник АВС и найдите середину стороны ВС – точку М.
2.Что называется серединой отрезка? …….
3.Соедините точку М с вершиной А. Отрезок АМ называется медианой треугольника.
4. Выучи определение:
Определение.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
5.Сколько вершин у треугольника? …..
6.Сколько у него сторон? ….
7.Сколько медиан можно построить в треугольнике?
8.Проведите все медианы в треугольнике.
9.Какое свойство медиан вы заметили?
(В любом треугольнике все медианы пересекаются в ……точке).
10.Эта точка называется центром тяжести треугольника.
11.О – точка пересечения медиан, называется замечательной точкой треугольника.
Опорный конспект для 2 группы:
1.Постройте треугольник АВС.
2.Теперь постройте биссектрису АА1 угла А с помощью транспортира.
3.Она пересечёт отрезок ВС в точке А1.
4.Отрезок АА1 называется биссектрисой угла А треугольника АВС.
5.Запомни определение:
Определение.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
6.Сколько вершин у треугольника? …..
7.Сколько у него углов? ….
8.Сколько биссектрис можно построить в треугольнике?
8.Проведите все биссектрисы треугольника.
9.Какое свойство биссектрис вы заметили?
(В любом треугольнике биссектрисы пересекаются в …… точке).
10. О – точка пересечения биссектрис, называется замечательной точкой треугольника.
12. точка О также является центром вписанной окружности в треугольнике.
(вставить рисунок)
Опорный конспект для 3 группы:
1.Какой отрезок называют перпендикуляром?
2. С помощью чего можно построить перпендикуляр из данной точки на данную прямую?
3.Начертите треугольник АВС
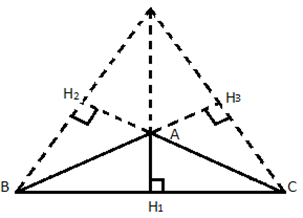
4.С помощью чертёжного угольника из вершины А проведите перпендикуляр АН к прямой ВС.
5.Он называется высотой треугольника.
6. Запомни определение:
Определение.
Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
7.Сколько высот имеет треугольник?..........
8.Постройте” все три высоты в треугольнике.
9.Какое свойство высоты вы заметили?
(В любом треугольнике высоты пересекаются в …… точке)
10. А если треугольник тупоугольный, то где находится точка пересечения высот этого треугольника?
11. А если треугольник прямоугольный, то где находится точка пересечения высот этого треугольника?
12. О – точка пересечения высот, называется замечательной точкой треугольника.
2) Обсуждение результатов исследования.
3)Релаксация. Презентация
«Предмет математики настолько серьезен, что не надо упускать случая делать её немного ……».(Пуассон)
К каким бы из данных элементов треугольника вы отнесли бы эти стих?
(Стихи иллюстрируются весёлым рисунком).
Эта дама-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.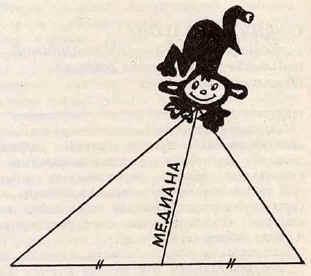 
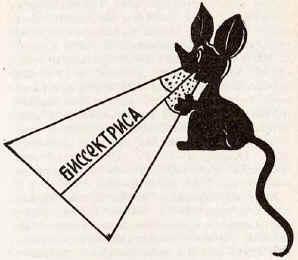
Луч этот – крыса,
Который бегает по углам
И делит угол пополам.
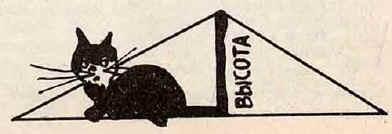
Она похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом
2)Физкульминутка для глаз (см флешку)
IV.Контроль усвоения материала. 1)Задание №2
Проверка в парах.
v. Работа в программе «Живая математика»
На рабочих столах компьютеров есть ярлык программы «Живая математика» давайте запустим программу на экран и ознакомимся с ней. В данной программе предоставляется возможность выполнять различные задания из геометрии на построение. У вас на столах задания для выполнения, просмотрите их.
Для этого выберем в меню левой части линию и нарисуем одну из сторон треугольника. затем обозначим точкой половину стороны треугольника. Далее выберем в меню кнопку с буквой «А» и обозначим вершины тругольника. Чтобы назвать вершины треугольника по заданию необходимо щелкнуть на букву обозначенной точки левой кнопкой мыши и в окне переименовать.
Задание 1. Построить медианы треугольника
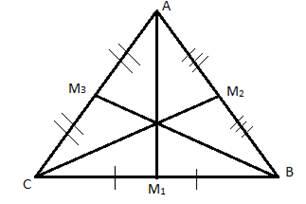А, В, С – вершины треугольника.
– середины сторон треугольника.
– медианы треугольника.
У каждого треугольника есть три медианы. Все медианы треугольника пересекаются в одной точке. И эта точка обладает замечательными свойствами и называется «центром тяжести» треугольника.
Задание 2. Построить биссектрисы треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. Стоит заметить, что биссектриса угла – это луч, делящий угол на два равных, а биссектриса треугольника – это отрезок, часть луча, ограниченная стороной треугольника.
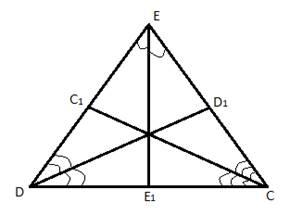
Рис. 2. Биссектрисы треугольника
C, D, E – вершины треугольника.
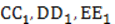– биссектрисы треугольника.
Три биссектрисы любого треугольника пересекаются в одной точке, которая также имеет важное свойство.
Задание 3.
Определение: Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
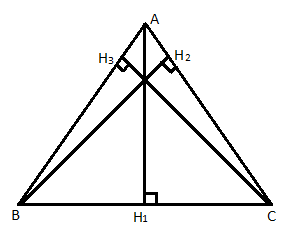
Рис. 3. Высоты остроугольного треугольника
А, В, С – вершины треугольника.
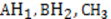– высоты треугольника.
У треугольника три вершины, а значит, и три высоты. Далее постройте высоты в тупоугольном треугольнике.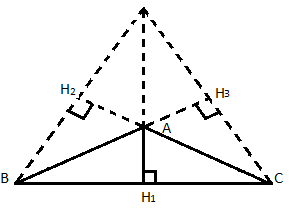 
Теперь мы научились строить медиану, биссектрису и высоты треугольника.
- Скажите а в какой программе можно еще сделать подобное построение?
(графический редактор, текстовый редактор с встроенным векторным редактором)
VI. Рефлексия.
Домашнее задание:
Задание 1. Медиана треугольника.
Задание 2. Биссектриса треугольника
Задание 3. Высота треугольника
Задание 1. Медиана треугольника.
Задание 2. Биссектриса треугольника
Задание 3. Высота треугольника
Получите свидетельство
Вход
Бинарный урок по математике и информатике "Медиана, биссектриса, высота треугольника" (0.79 MB)
0
1262
53
Нравится
0
