Понятие «функция» часто используется при изучении реальных процессов в природе, науке и технике. Само понятие «функция» возникло в XVII веке и прошло сложный и трудный путь развития. Среди ученых, внесших большой вклад в развитие представлений о функции, были Г.В. Лейбниц (немецкий философ и математик), И. Ньютон (английский физик и математик), Л. Эйлер (швейцарец по происхождению, многие годы живший и работавший в России по приглашению Екатерины II), Н.И. Лобачевский (русский математик), Л. Дирихле (немецкий математик), А.Н. Колмогоров (советский математик) и др. На практике изменение одной величины обычно связано с изменением одной или нескольких других величин.
Функция является заданной, иначе говоря, известной, если для каждого значения возможного числа аргументов можно узнать соответствующее значение функции. Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.
1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней) , основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента.
Аргумент х принимает заданные в таблице значения, а у определяется соответственно этому аргументу х.
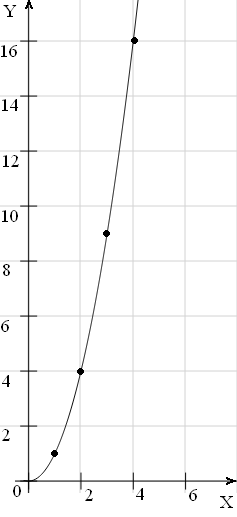
2. Графический способ заключается в проведении линии (графика) , у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными.
Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.
Например:
Функцию можно задать с помощью математической формулы y=x2, тогда если х равно 2, то у равно 4, возводим х в квадрат.
4. Словесный способ состоит в задании функции обычным языком, т. е. словами. При этом необходимо дать входные, выходные значения и соответствие между ними.
Например:
Словесно можно задать функцию (задачу) , принимающуюся в виде натурального аргумента х с соответствующим значением суммы цифр, из которых состоит значение у. Поясняем: если х равно 4, то у равно 4, а если х равно 358, то у равен сумме 3 + 5 + 8, т. е 16. Далее аналогично.
5. Рекурсивный способ состоит в задании функции через саму себя, при этом значения функции определяются через другие ее же значения. Такой способ задания функции используется в задании множеств и рядов.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Материал по математике на тему "Задание функции несколькими способами" (28.27 КB)
Материал по математике на тему "Задание функции несколькими способами" (28.27 КB)
 0
0 1501
1501 104
104 Нравится
0
Нравится
0


