Решение неравенств.
Два неравенства, содержащие одни и те же неизвестные, называются равносильными, если они справедливы при одних и тех же значениях этих неизвестных. Такое же определение используется для равносильности двух систем неравенств. Решение неравенств - это процесс перехода от одного неравенства к другому, равносильному неравенству. Для этого используются основные свойства неравенств (см. параграф "Неравенства: общие сведения"). Кроме того, может быть использована замена любого выражения другим, тождественным данному. Неравенства могут быть алгебраические (содержащие только многочлены) и трансцендентные (например, логарифмические или тригонометрические). Мы рассмотрим здесь один очень важный метод, используемый часто при решении алгебраических неравенств.
Метод интервалов.
Решить неравенство: (x – 3) (x – 5) < 2(x – 3). Здесь нельзя делить обе части неравенства на (x – 3), так как мы не знаем знака этого двучлена (он содержит неизвестное x). Поэтому мы перенесём все члены неравенства в левую часть:
(x – 3) (x – 5) – 2(x – 3) < 0,
разложим её на множители:
(x – 3) (x – 5 – 2) < 0,
и получим: (x – 3) (x – 7) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что x = 3 и x = 7 - корни этого выражения. Поэтому вся числовая ось разделится этими корнями на следующие три интервала:
В интервале I (x < 3) оба сомножителя отрицательны, следовательно, их произведение положительно; в интервале II (3 < x < 7) первый множитель (x – 3) положителен, а второй (x – 7) отрицателен, поэтому их произведение отрицательно; в интервале III (x > 7) оба сомножителя положительны, следовательно, их произведение также положительно. Теперь остаётся выбрать интервал, в котором наше произведение отрицательно. Это интервал II, следовательно, решение неравенства: 3 < x < 7. Последнее выражение - так называемое двойное неравенство. Оно означает, что x должен быть одновременно больше 3 и меньше 7.
Пример. Решить следующее неравенство методом интервалов:
(x – 1) (x – 2) (x – 3) … (x –100) > 0.

Решение. Корни левой части неравенства очевидны: 1, 2, 3, …, 100.
Они разбивают числовую ось на 101 интервал:
Так как количество скобок в левой части чётно (равно 100), то при x < 1, когда все множители отрицательны, их произведение положительно. При переходе через корень происходит смена знака произведения. Поэтому следующим интервалом, внутри которого произведение положительно, будет (2, 3), затем (4, 5), затем (6, 7), …, (98, 99) и наконец, x >100.
Таким образом, данное неравенство имеет решение:
x < 1, 2 < x < 3, 4 < x < 5,…, x >100.
Итак, чтобы решить алгебраическое неравенство, надо перенести все его члены в левую (или правую) часть и решить соответствующее уравнение. После этого найденные корни нанести на числовую ось; в результате она разбивается на некоторое число интервалов. На последнем этапе решения нужно определить, какой знак имеет многочлен внутри каждого из этих интервалов, и выбрать нужные интервалы в соответствии со знаком решаемого неравенства.
Заметим, что большинство трансцендентных неравенств заменой неизвестного приводятся к алгебраическому неравенству. Его надо решить относительно нового неизвестного, а затем путём обратной замены найти решение для исходного неравенства.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


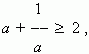 где a – положительное число.
где a – положительное число.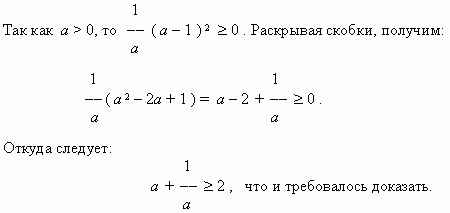
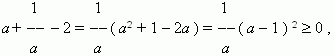
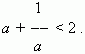
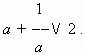
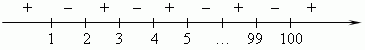









 Материал по математике "Доказательство неравенств" (27.65 КB)
Материал по математике "Доказательство неравенств" (27.65 КB)
 0
0 1137
1137 57
57 Нравится
0
Нравится
0