| № п/п | Тема раздела, урока | Кол-во часов
| Тип урока | Вид работы | Элементы содержания урока | Требования к уровню подготовки обучающихся | Формы контроля |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
| Неравенства и их системы | 2 | Основная цель: - понимать смысл понятия доказательство неравенств и его отличие от решения неравенств; - формирование умений по использованию своих знаний в доказательстве неравенств; - развивать логическое мышление
|
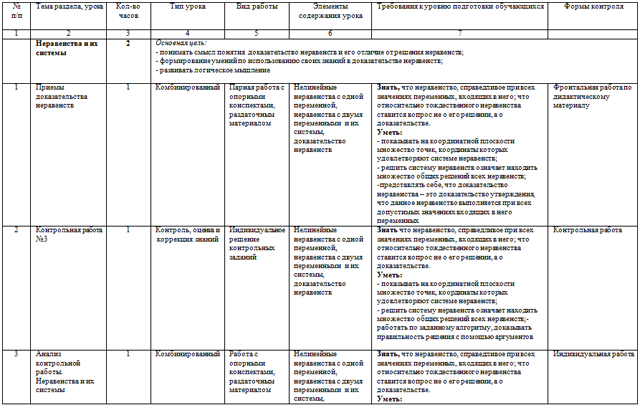
| 1 | Приемы доказательства неравенств | 1 | Комбинированный | Парная работа с опорными конспектами, раздаточным материалом | Нелинейные неравенства с одной переменной, неравенства с двумя переменными и их системы, доказательство неравенств | Знать, что неравенство, справедливое при всех значениях переменных, входящих в него; что относительно тождественного неравенства ставится вопрос не о его решении, а о доказательстве. Уметь: - показывать на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств; - решить систему неравенств означает находить множество общих решений всех неравенств; -представлять себе, что доказательство неравенства – это доказательство утверждения, что данное неравенство выполняется при всех допустимых значениях входящих в него переменных | Фронтальная работа по дидактическому материалу |
| 2 | Контрольная работа №3 | 1 | Контроль, оценка и коррекция знаний | Индивидуальное решение контрольных заданий | Нелинейные неравенства с одной переменной, неравенства с двумя переменными и их системы, доказательство неравенств | Знать что неравенство, справедливое при всех значениях переменных, входящих в него; что относительно тождественного неравенства ставится вопрос не о его решении, а о доказательстве. Уметь: - показывать на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств; - решить систему неравенств означает находить множество общих решений всех неравенств;- работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Контрольная работа |
| 3 | Анализ контрольной работы. Неравенства и их системы | 1 | Комбинированный | Работа с опорными конспектами, раздаточным материалом | Нелинейные неравенства с одной переменной, неравенства с двумя переменными и их системы, доказательство неравенств | Знать, что неравенство, справедливое при всех значениях переменных, входящих в него; что относительно тождественного неравенства ставится вопрос не о его решении, а о доказательстве. Уметь: - показывать на координатной плоскости множество точек, координаты которых удовлетворяют системе неравенств; - решить систему неравенств означает находить множество общих решений всех неравенств; -представлять себе, что доказательство неравенства – это доказательство утверждения, что данное неравенство выполняется при всех допустимых значениях входящих в него переменных | Индивидуальная работа |
| 4 | Числовая последовательность и способы ее задания | 1 | Учебный практикум | Составление опорного конспекта, решение задач | Числовая последовательность и способы ее задания | Знать, что такое область определения и область значений функции Уметь - понимать понятие числовой последовательности; - понимать смысл различных способов задания последовательности; - аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их; - развернуто обосновывать суждения
| Фронтальная работа |
| 5 | Виды числовой последовательности | 1 | Комбинированный, поисковый | Работа с конспектом с книгой и наглядными пособиями по группам | Числовая последовательность и способы ее задания | Знать, что такое область определения и область значений функции Уметь - понимать понятие числовой последовательности; - понимать смысл различных способов задания последовательности; - определять понятия, приводить доказательства - применять правила и свойства при решении задач | Фронтальная работа |
|
| Арифметическая прогрессия | 8 | Основная цель: - формирование определения арифметической прогрессии; - понимать выведения формулы n - го члена арифметической прогрессии; - формирование знаний о формуле суммы n членов арифметической прогрессии и умений по использованию этой формулы - развивать логическое мышление
|
| 6 | Арифметическая прогрессия. Формула n - го члена арифметической прогрессии | 1 | Учебный практикум | Составление опорного конспекта, решение задач | Арифметическая прогрессия. Формула n - го члена арифметической прогрессии и свойства | Знать определение и свойства арифметической прогрессии. Уметь: - применять формулу n - го члена арифметической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 7 | Свойства арифметической прогрессии | 1 | Комбинированный | Решение упражнений, составление опорного конспекта | Арифметическая прогрессия. Формула n - го члена арифметической прогрессии и свойства | Знать определение и свойства арифметической прогрессии. Уметь: - применять формулу n - го члена арифметической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 8 | Задачи по применению свойств арифметической прогрессии | 1 | Поисковый | Работа с опорными конспектами, раздаточным материалом, в группах | Арифметическая прогрессия. Формула n - го члена арифметической прогрессии и свойства | Знать определение и свойства арифметической прогрессии. Уметь: - применять формулу n - го члена арифметической прогрессии и свойства - расширять и обобщать формулу и свойства арифметической прогрессии - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Самостоятельная работа |
| 9 | Формула суммы первых n членов арифметической прогрессии | 1 | Поисковый | Работа с опорными конспектами, раздаточным материалом, в группах | Формула n - го члена и суммы первых n членов арифметической прогрессии и свойства. | Знать формулы n - го члена и суммы первых n членов арифметической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов арифметической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 10 | Применение формул суммы первых n членов арифметической прогрессии. Самостоятельная работа | 1 | Комбинированный | Решение упражнений, составление опорного конспекта | Формула n - го члена и суммы первых n членов арифметической прогрессии и свойства | Знать формулы n - го члена и суммы первых n членов арифметической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов арифметической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Самостоятельная работа по карточкам |
| 11 | Решение задач с помощью формул суммы первых n членов арифметической прогрессии | 1 | Комбинированный | Решение упражнений, составление опорного конспекта | Формула n - го члена и суммы первых n членов арифметической прогрессии и свойства | Знать формулы n - го члена и суммы первых n членов арифметической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов арифметической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 12 | Контрольная работа № 4 | 1 | Контроль, оценка и коррекция знаний | Индивидуальное решение контрольных заданий | Формула n - го члена и суммы первых n членов арифметической прогрессии и свойства | Знать формулы n - го члена и суммы первых n членов арифметической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов арифметической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Контрольная работа |
| 13 | Анализ контрольной работы. Арифметическая прогрессия | 1 | Комбинированный | Парная работа с раздаточным материалом | Формула n - го члена и суммы первых n членов арифметической прогрессии и свойства | Уметь: - расширять и обобщать сведения об арифметической прогрессии и ее свойствах; - владеть навыками контроля и оценки своей деятельности, предвидеть возможные последствия своих действий. | Индивидуальная работа |
|
| Геометрическая прогрессия | 8 | Основная цель: - формирование определения геометрической прогрессии; - понимать выведения формулы n - го члена геометрической прогрессии; - формирование знаний о формуле суммы n членов, бесконечно убывающей геометрической прогрессии и умений по использованию этих формул - развивать логическое мышление |
| 14 | Геометрическая прогрессия. Формула n-го члена геометрической прогрессии | 1 | Проблемно -поисковый | Работа с опорными конспектами, раздаточным материалом, в группах | Геометрическая прогрессия. Формула n - го члена геометрической прогрессии и свойства | Знать определение и свойства геометрической прогрессии. Уметь: - применять формулу n - го члена геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Групповая работа |
| 15 | Свойства геометрической прогрессии | 1 | Комбинированный | Решение упражнений, составление опорного конспекта | Геометрическая прогрессия. Формула n - го члена геометрической прогрессии и свойства | Знать определение и свойства геометрической прогрессии. Уметь: - применять формулу n - го члена геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 16 | Решение геометрической прогрессии | 1 | Поисковый | Работа с опорными конспектами, раздаточным материалом, в группах | Геометрическая прогрессия. Формула n - го члена геометрической прогрессии и свойства | Знать определение и свойства геометрической прогрессии. Уметь: - применять формулу n - го члена геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 17 | Формула суммы первых n членов геометрической прогрессии | 1 | Поисковый | Составление опорного конспекта, решение задач | Формула n - го члена и суммы первых n членов геометрической прогрессии и свойства | Знать определение, свойства и формулы геометрической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Фронтальная работа |
| 18 | Применение формул суммы первых n членов геометрической прогрессии | 1 | Комбинированный | Работа с опорными конспектами, раздаточным материалом, в группах | Формула n - го члена и суммы первых n членов геометрической прогрессии и свойства | Знать определение, свойства и формулы геометрической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Дифференцированная самостоятельная работа по раздаточным материалам |
| 19 | Решение задач с помощью формул суммы первых n членов геометрической прогрессии. Самостоятельная работа | 1 | Комбинированный, поисковый | Работа с опорными конспектами, раздаточным материалом, по парам | Формула n - го члена и суммы первых n членов геометрической прогрессии и свойства | Знать определение, свойства и формулы геометрической прогрессии. Уметь: - применять формулу n - го члена и суммы первых n членов геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Парная работа по дидактическому материалу |
| 20 | Формула суммы бесконечно убывающей геометрической прогрессии | 1 | Проблемно -поисковый | Составление опорного конспекта, решение задач | Формула n - го члена, суммы первых n членов и суммы бесконечно убывающей геометрической прогрессии и свойства | Знать определение, свойства и формулы геометрической прогрессии. Уметь: - применять формулу n - го члена, суммы первых n членов суммы бесконечно убывающей геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Индивидуальная работа |
| 21 | Применение формул суммы бесконечно убывающей геометрической прогрессии | 1 | Комбинированный | Решение упражнений, составление опорного конспекта, в группах | Формула n - го члена, суммы первых n членов и суммы бесконечно убывающей геометрической прогрессии и свойства | Знать определение, свойства и формулы геометрической прогрессии. Уметь: - применять формулу n - го члена, суммы первых n членов суммы бесконечно убывающей геометрической прогрессии и свойства - работать по заданному алгоритму, доказывать правильность решения с помощью аргументов
| Групповая работа |

 Получите свидетельство
Получите свидетельство Вход
Вход











 Среднесрочное планирование по алгебре (9 класс) (88.5 КB)
Среднесрочное планирование по алгебре (9 класс) (88.5 КB)
 0
0 834
834 211
211 Нравится
0
Нравится
0



