Арифметическим корнем n-й степени из неотрицательного числа a называется неотрицательное число b, n-я степень которого равна a.
Записывается так:
n√a=b, nЄN, n≥2.
Эта запись означает, что bn = a, где b и a – неотрицательные числа.
Число n называется показателем степени корня, число а – подкоренным выражением, b – значением арифметического корня n-й степени.
Операция нахождения значения корня называется извлечением корня.
Корней чётной степени из отрицательных чисел не существует.
Корнем нечётной степени из отрицательного числа а называется такое отрицательное число b, которое при его возведении в эту нечётную степень равно числу а.

Для корней нечётной степени справедливо равенство:
2k+1√-a=-2k+1√a, a≥0, kЄN.
Свойства корней.
Для положительных а и b, натуральных n и k (n ≥ 2, k ≥ 2), целого m выполняются следующие соотношения.
(n√a)n=a
n√a*b=n√a*n√b
n√a/b=n√a/n√b
nk√amk=n√am
(n√a)m=(n√am)
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


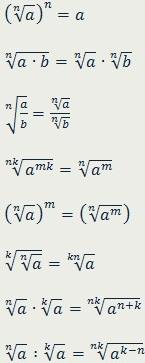 Кроме того, для любого числа а верно:
Кроме того, для любого числа а верно:








 Материал по математике "Арифметический корень" (45.62 КB)
Материал по математике "Арифметический корень" (45.62 КB)
 0
0 732
732 4
4 Нравится
0
Нравится
0






