Алгебра 10 класс
Тема урока: Свойства тригонометрических функций
Савичев Владимир Александрович,
учитель математики, I категория,
МБОУ Староюрковичская СОШ
Цели урока: Повторить и систематизировать изученный материал, подготовиться к контрольной работе.
Тип урока: Урок-обобщение темы.
Оборудование: Компьютер, проектор, экран, презентация к уроку, раздаточный материал.
Замечание! В презентации к уроку используется анимация, поэтому на слайдах 4-7 слова текста не перемещать. Презентацию просматривать в режиме показа слайдов.
Ход урока.
- Оргмомент.
Приветствие. Знакомство с темой урока (слайд 1).
- Повторение материала.
– С какими функциями мы работали на последних уроках алгебры?
(тригонометрическими: синус, косинус, тангенс, котангенс; дается определение, слайд 2)
Числовые функции, заданные формулами y=sinx, y=cosx, y=tgx, y=ctgx, называют соответственно синусом, косинусом, тангенсом и котангенсом.
- Систематизация материала.
– Свойства тригонометрических функций удобно рассматривать, опираясь на схему исследования тригонометрической функции. Давайте вспомним эту схему.
(слайд 3, учащиеся поэтапно называют пункты схемы исследования, учитель по щелчку мыши выводит на экран названные пункты)
1.1 – область определения;
1.2 – область значений;
2.1 – четность (нечетность);
2.2 – наименьший положительный период;
3.1 – координаты точек пересечения графика f с осью Ох;
3.2 – координаты точек пересечения графика f с осью Оу;
4.1 – промежутки, на которых f принимает положительные значения;
4.2 – промежутки, на которых f принимает отрицательные значения;
5.1 – промежутки возрастания;
5.2 – промежутки убывания;
6.1 – точки минимума;
6.2 – минимумы функции;
6.3 – точки максимума;
6.4 – максимумы функции.
– Повторим свойства каждой тригонометрической функции. Рассмотрим график функции f(x)=sinx.
(слайд 4, на слайде изображен график функции f(x)=sinx, с помощью которого учащиеся проводят исследование функции согласно схеме исследования: по щелчку мыши появляется пункт рассмотренной схемы, и учащиеся определяют ответ, после чего учитель выводит его на экран)
Функция y=sinx

1.1 – область определения R
1.2 – область значений
2.1 – четность (нечетность)
2.2 – наименьший положительный период p
3.1 – координаты точек пересечения графика f с осью Ох (pn; 0)
3.2 – координаты точек пересечения графика f с осью Оу (0; 0)
4.1 – промежутки, на которых f принимает положительные значения
pn; p+ 2pn), nÎZ
4.2 – промежутки, на которых f принимает отрицательные значения
p+2pn; 2pn), nÎZ
5.1 – промежутки возрастания p/2+2pn; p/2+2pn], nÎZ
5.2 – промежутки убывания p/2+2pn; 3p/2+2pn], nÎZ
6.1 – точки минимума p/2+2pn, nÎZ
6.2 – минимумы функции
6.3 – точки максимума p/2+2pn, nÎZ
6.4 – максимумы функции
– Аналогичный процесс повторяем, рассматривая график функции f(x)=cosx.
(слайд 5, на слайде изображен график функции f(x)=cosx, с помощью которого учащиеся проводят исследование функции согласно схеме исследования: по щелчку мыши появляется пункт рассмотренной схемы, и учащиеся определяют ответ, после чего учитель выводит его на экран)
Функция y=cosx

1.1 – область определения R
1.2 – область значений
2.1 – четность (нечетность)
2.2 – наименьший положительный период p
3.1 – координаты точек пересечения графика f с осью Ох (p/2+pn;0),nÎZ
3.2 – координаты точек пересечения графика f с осью Оу (0; 1)
4.1 – промежутки, на которых f принимает положительные значения
p/2+2pn; p/2+2pn), nÎZ
4.2 – промежутки, на которых f принимает отрицательные значения
p/2+2pn; 3p/2+2pn), nÎZ
5.1 – промежутки возрастания p+2pn; 2pn], nÎZ
5.2 – промежутки убывания pn; p+2pn], nÎZ
6.1 – точки минимума p+2pn, nÎZ
6.2 – минимумы функции
6.3 – точки максимума pn, nÎZ
6.4 – максимумы функции
Далее рассматриваются слайды 6 и 7 с графиками функций f(x)=tgx и f(x)=сtgx.
Функция y=tgx

1.1 – область определения p/2+pn; p/2+pn), nÎZ
1.2 – область значений R
2.1 – четность (нечетность)
2.2 – наименьший положительный период p
3.1 – координаты точек пересечения графика f с осью Ох (pn;0), nÎZ
3.2 – координаты точек пересечения графика f с осью Оу (0; 0)
4.1 – промежутки, на которых f принимает положительные значения
pn; p/2+pn), nÎZ
4.2 – промежутки, на которых f принимает отрицательные значения
p/2+pn; pn), nÎZ
5.1 – промежутки возрастания p/2+pn; p/2+pn), nÎZ
5.2 – промежутки убывания
6.1 – точки минимума
6.2 – минимумы функции
6.3 – точки максимума
6.4 – максимумы функции
Функция y=ctgx

1.1 – область определения pn; p+pn), nÎZ
1.2 – область значений R
2.1 – четность (нечетность)
2.2 – наименьший положительный период p
3.1 – координаты точек пересечения графика f с осью Ох (p/2+pn;0),nÎZ
3.2 – координаты точек пересечения графика f с осью Оу нет
4.1 – промежутки, на которых f принимает положительные значения
pn; p/2+pn), nÎZ
4.2 – промежутки, на которых f принимает отрицательные значения
p/2+pn; pn), nÎZ
5.1 – промежутки возрастания
5.2 – промежутки убывания pn; p+pn), nÎZ
6.1 – точки минимума
6.2 – минимумы функции
6.3 – точки максимума
6.4 – максимумы функции
- Подготовка к контрольной работе.
Учащиеся выполняют тестовые задания на повторение основных свойств тригонометрических функций с последующей самопроверкой по ключу (слайды 8 и 9).
Тестовые задания
- Областью значений функции g(x)=2cos2x-2 является промежуток:
а) [-2; 2] б) [0; 2] в) [-2; 0]
- Областью значений функции t(x)=3cos2x-3 является промежуток:
а) [-3; 3] б) [0; 3] в) [-3; 0]
- График функции, изображенный на рисунке, задается формулой:

- ) y=sin0,5x б) y=2sinx в) y=-2sinx
- График функции, изображенный на рисунке, задается формулой:

- ) y=cos2x б) y=-0,5cosx в) y=0,5cosx
- Функция y=-cosx+1 возрастает на промежутках:
а) [2pn; p+2pn], nÎZ
б) [-p+2pn; 2pn], nÎZ
- ) [-p/2+2pn; 3p/2+2pn], nÎZ
- Функция y=sinx+1 убывает на промежутках:
а) [p/2+2pn; 3p/2+2pn], nÎZ
б) [-p/2+2pn; p/2+2pn], nÎZ
в) [p+2pn; 2p+2pn], nÎZ
Ответы для самопроверки тестовых заданий
- в
- в
- в
- б
- а
- а
Затем выполняют дополнительные задания на повторение тригонометрических функций числового аргумента с дальнейшей взаимопроверкой по ключу (слайды 10-12).
Дополнительные задания
- Даны функции f(x)=cos3x×sin2x и g(x)=cos2x×sin3x. Если x=p/3, то
а)  б)
б)  в)
в) 
- Даны функции g(x)=sin2x×cos4x и f(x)=cos2x×sin4x. Если x=-p/8, то
а)  б)
б)  в)
в) 
- Выражение
 тождественно равно:
тождественно равно:
а) cos2α б) 1-sinα в) 1
- Выражение
 тождественно равно:
тождественно равно:
а) 1 б) sin2α в) 1-cosα
- Значение выражения
 при
при  равно:
равно:
а) 2 б) 1 в) -0,5
- Значение выражения
 при
при  равно:
равно:
а) -0,5 б) 0,5 в) 1
Ключ к дополнительным заданиям:
- б
- б
- в
- а
- а
- б
- Подведение итогов урока.
- Рефлексия.
- Домашнее задание.

Староюрковичская средняя школа
Алгебра 10 класс
Свойства тригонометрических функций
Учитель: Савичев В. А.

Определение
- Числовые функции, заданные формулами y =sin x , y =cos x , y =tg x , y =ctg x , называют соответственно синусом, косинусом, тангенсом и котангенсом.

Схема исследования тригонометрических функций
1.1 – область определения;
1.2 – область значений;
2.1 – четность (нечетность);
2.2 – наименьший положительный период;
3.1 – координаты точек пересечения графика f с осью Ох;
3.2 – координаты точек пересечения графика f с осью Оу;
4.1 – промежутки, на которых f принимает положительные значения;
4.2 – промежутки, на которых f принимает отрицательные значения;
5.1 – промежутки возрастания;
5.2 – промежутки убывания;
6.1 – точки минимума;
6.2 – минимумы функции;
6.3 – точки максимума;
6.4 – максимумы функции.
![Функция y =sin x R 3.1 - координаты точек пересечения графика 1.1 - область определения: 5.1 - промежутки возрастания: 2.1 - четность (нечетность): 4.1 - промежутки, на которых функция принимает 6.1 - точки минимума: нечетная (2 π n; π+2πn), n Z ( π n; 0), n Z функции f с осью Ох: 6.2 - минимумы функции: положительные значения: -1 2 π [-1; 1] 4.2 - промежутки, на которых функция принимает 5.2 - промежутки убывания: 3.2 - координаты точек пересечения графика 2.2 - наименьший положительный период: 1.2 - область значений: 6.3 - точки максимума: ( 0; 0) (- π+ 2πn; 2πn), n Z 6.4 - максимумы функции: функции f с осью Оy: отрицательные значения: 1](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img3.jpg)
Функция y =sin x
R
3.1 - координаты точек пересечения графика
1.1 - область определения:
5.1 - промежутки возрастания:
2.1 - четность (нечетность):
4.1 - промежутки, на которых функция принимает
6.1 - точки минимума:
нечетная
(2 π n; π+2πn), n Z
( π n; 0), n Z
функции f с осью Ох:
6.2 - минимумы функции:
положительные значения:
-1
2 π
[-1; 1]
4.2 - промежутки, на которых функция принимает
5.2 - промежутки убывания:
3.2 - координаты точек пересечения графика
2.2 - наименьший положительный период:
1.2 - область значений:
6.3 - точки максимума:
( 0; 0)
(- π+ 2πn; 2πn), n Z
6.4 - максимумы функции:
функции f с осью Оy:
отрицательные значения:
1
![Функция y =cos x π+2π n, n Z R 3.1 - координаты точек пересечения графика 1.1 - область определения: 5.1 - промежутки возрастания: 2.1 - четность (нечетность): 4.1 - промежутки, на которых функция принимает 6.1 - точки минимума: четная [- π+2 πn; 2πn], n Z функции f с осью Ох: 6.2 - минимумы функции: положительные значения: -1 2 π 2π n, n Z [-1; 1] 3.2 - координаты точек пересечения графика 4.2 - промежутки, на которых функция принимает 5.2 - промежутки убывания: 2.2 - наименьший положительный период: 1.2 - область значений: 6.3 - точки максимума: [2 π n; π+2πn], n Z ( 0; 1) функции f с осью Оy: 6.4 - максимумы функции: отрицательные значения: 1](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img4.jpg)
Функция y =cos x
π+2π n, n Z
R
3.1 - координаты точек пересечения графика
1.1 - область определения:
5.1 - промежутки возрастания:
2.1 - четность (нечетность):
4.1 - промежутки, на которых функция принимает
6.1 - точки минимума:
четная
[- π+2 πn; 2πn], n Z
функции f с осью Ох:
6.2 - минимумы функции:
положительные значения:
-1
2 π
2π n, n Z
[-1; 1]
3.2 - координаты точек пересечения графика
4.2 - промежутки, на которых функция принимает
5.2 - промежутки убывания:
2.2 - наименьший положительный период:
1.2 - область значений:
6.3 - точки максимума:
[2 π n; π+2πn], n Z
( 0; 1)
функции f с осью Оy:
6.4 - максимумы функции:
отрицательные значения:
1
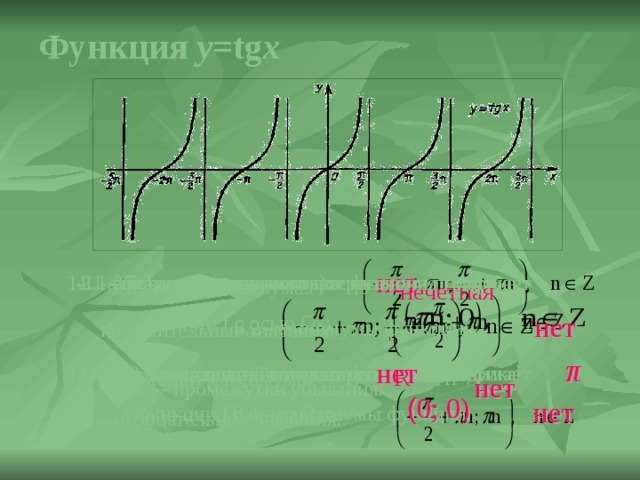
Функция y =tg x
нет
3.1 - координаты точек пересечения графика
5.1 - промежутки возрастания:
2.1 - четность (нечетность):
1.1 - область определения:
4.1 - промежутки, на которых функция принимает
6.1 - точки минимума:
нечетная
функции f с осью Ох:
нет
6.2 - минимумы функции:
положительные значения:
π
нет
3.2 - координаты точек пересечения графика
4.2 - промежутки, на которых функция принимает
2.2 - наименьший положительный период:
1.2 - область значений:
R
6.3 - точки максимума:
нет
5.2 - промежутки убывания:
( 0; 0)
нет
6.4 - максимумы функции:
функции f с осью Оy:
отрицательные значения:

Функция y =ctg x
нет
нет
5.1 - промежутки возрастания:
2.1 - четность (нечетность):
1.1 - область определения:
3.1 - координаты точек пересечения графика
4.1 - промежутки, на которых функция принимает
6.1 - точки минимума:
нечетная
функции f с осью Ох:
нет
6.2 - минимумы функции:
положительные значения:
5.2 - промежутки убывания:
π
нет
4.2 - промежутки, на которых функция принимает
3.2 - координаты точек пересечения графика
2.2 - наименьший положительный период:
1.2 - область значений:
R
6.3 - точки максимума:
нет
нет
функции f с осью Оy:
6.4 - максимумы функции:
отрицательные значения:
![Тестовые задания Областью значений функции g(x)=2cos2x-2 является промежуток: а) [-2; 2] б) [0; 2] в) [-2; 0] Областью значений функции t(x)=3cos2x-3 является промежуток: а) [-3; 3] б) [0; 3] в) [-3; 0] График функции, изображенный на рисунке, задается формулой: а) y=sin0,5x б) y=2sinx в) y=-2sinx График функции, изображенный на рисунке, задается формулой: а) y=cos2x б) y=-0,5cosx в) y=0,5cosx Функция y=-cosx+1 возрастает на промежутках: а) [2 n; +2 n], n Z б) [- +2 n; 2 n], n Z в) [- /2+2 n; 3 /2+2 n], n Z Функция y=sinx+1 убывает на промежутках: а) [ /2+2 n; 3 /2+2 n], n Z б) [- /2+2 n; /2+2 n], n Z в) [ +2 n; 2 +2 n], n Z](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img7.jpg)
Тестовые задания
- Областью значений функции g(x)=2cos2x-2 является промежуток:
а) [-2; 2] б) [0; 2] в) [-2; 0]
- Областью значений функции t(x)=3cos2x-3 является промежуток:
а) [-3; 3] б) [0; 3] в) [-3; 0]
- График функции, изображенный на рисунке, задается формулой:
а) y=sin0,5x б) y=2sinx в) y=-2sinx
- График функции, изображенный на рисунке, задается формулой:
а) y=cos2x б) y=-0,5cosx в) y=0,5cosx
- Функция y=-cosx+1 возрастает на промежутках:
а) [2 n; +2 n], n Z
б) [- +2 n; 2 n], n Z
в) [- /2+2 n; 3 /2+2 n], n Z
- Функция y=sinx+1 убывает на промежутках:
а) [ /2+2 n; 3 /2+2 n], n Z
б) [- /2+2 n; /2+2 n], n Z
в) [ +2 n; 2 +2 n], n Z
![Ответы для самопроверки Областью значений функции g(x)=2cos2x-2 является промежуток: в) [-2; 0] Областью значений функции t(x)=3cos2x-3 является промежуток: в) [-3; 0] График функции, изображенный на рисунке, задается формулой: в) y=-2sinx График функции, изображенный на рисунке, задается формулой: б) y=-0,5cosx Функция y=-cosx+1 возрастает на промежутках: а) [2 n; +2 n], n Z Функция y=sinx+1 убывает на промежутках: а) [ /2+2 n; 3 /2+2 n], n Z](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img8.jpg)
Ответы для самопроверки
- Областью значений функции g(x)=2cos2x-2 является промежуток:
в) [-2; 0]
- Областью значений функции t(x)=3cos2x-3 является промежуток:
в) [-3; 0]
- График функции, изображенный на рисунке, задается формулой:
в) y=-2sinx
- График функции, изображенный на рисунке, задается формулой:
б) y=-0,5cosx
- Функция y=-cosx+1 возрастает на промежутках:
а) [2 n; +2 n], n Z
- Функция y=sinx+1 убывает на промежутках:
а) [ /2+2 n; 3 /2+2 n], n Z
 g( /3) б) f( /3) /3) в) f( /3)=g( /3) Даны функции g(x)=sin2x cos4x и f(x)=cos2x sin4x. Если x=- /8, то а) g(- /8) /8) б) g(- /8)f(- /8) в) g(- /8)=f(- /8) Выражение тождественно равно: а) cos2α б) 1-sinα в) 1 Выражение тождественно равно: а) 1 б) sin2α в) 1-cosα " width="640"
g( /3) б) f( /3) /3) в) f( /3)=g( /3) Даны функции g(x)=sin2x cos4x и f(x)=cos2x sin4x. Если x=- /8, то а) g(- /8) /8) б) g(- /8)f(- /8) в) g(- /8)=f(- /8) Выражение тождественно равно: а) cos2α б) 1-sinα в) 1 Выражение тождественно равно: а) 1 б) sin2α в) 1-cosα " width="640"
Дополнительные задания
- Даны функции f(x)=cos3x sin2x и g(x)=cos2x sin3x.
Если x= /3, то
а) f( /3)g( /3) б) f( /3) /3) в) f( /3)=g( /3)
- Даны функции g(x)=sin2x cos4x и f(x)=cos2x sin4x.
Если x=- /8, то
а) g(- /8) /8) б) g(- /8)f(- /8) в) g(- /8)=f(- /8)
- Выражение тождественно равно:
а) cos2α б) 1-sinα в) 1
- Выражение тождественно равно:
а) 1 б) sin2α в) 1-cosα

Дополнительные задания
- Значение выражения при равно:
а) 2 б) 1 в) -0,5
- Значение выражения при равно:
а) -0,5 б) 0,5 в) 1

Ключ для взаимопроверки дополнительных заданий

Конец



![Функция y =sin x R 3.1 - координаты точек пересечения графика 1.1 - область определения: 5.1 - промежутки возрастания: 2.1 - четность (нечетность): 4.1 - промежутки, на которых функция принимает 6.1 - точки минимума: нечетная (2 π n; π+2πn), n Z ( π n; 0), n Z функции f с осью Ох: 6.2 - минимумы функции: положительные значения: -1 2 π [-1; 1] 4.2 - промежутки, на которых функция принимает 5.2 - промежутки убывания: 3.2 - координаты точек пересечения графика 2.2 - наименьший положительный период: 1.2 - область значений: 6.3 - точки максимума: ( 0; 0) (- π+ 2πn; 2πn), n Z 6.4 - максимумы функции: функции f с осью Оy: отрицательные значения: 1](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img3.jpg)
![Функция y =cos x π+2π n, n Z R 3.1 - координаты точек пересечения графика 1.1 - область определения: 5.1 - промежутки возрастания: 2.1 - четность (нечетность): 4.1 - промежутки, на которых функция принимает 6.1 - точки минимума: четная [- π+2 πn; 2πn], n Z функции f с осью Ох: 6.2 - минимумы функции: положительные значения: -1 2 π 2π n, n Z [-1; 1] 3.2 - координаты точек пересечения графика 4.2 - промежутки, на которых функция принимает 5.2 - промежутки убывания: 2.2 - наименьший положительный период: 1.2 - область значений: 6.3 - точки максимума: [2 π n; π+2πn], n Z ( 0; 1) функции f с осью Оy: 6.4 - максимумы функции: отрицательные значения: 1](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img4.jpg)


![Тестовые задания Областью значений функции g(x)=2cos2x-2 является промежуток: а) [-2; 2] б) [0; 2] в) [-2; 0] Областью значений функции t(x)=3cos2x-3 является промежуток: а) [-3; 3] б) [0; 3] в) [-3; 0] График функции, изображенный на рисунке, задается формулой: а) y=sin0,5x б) y=2sinx в) y=-2sinx График функции, изображенный на рисунке, задается формулой: а) y=cos2x б) y=-0,5cosx в) y=0,5cosx Функция y=-cosx+1 возрастает на промежутках: а) [2 n; +2 n], n Z б) [- +2 n; 2 n], n Z в) [- /2+2 n; 3 /2+2 n], n Z Функция y=sinx+1 убывает на промежутках: а) [ /2+2 n; 3 /2+2 n], n Z б) [- /2+2 n; /2+2 n], n Z в) [ +2 n; 2 +2 n], n Z](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img7.jpg)
![Ответы для самопроверки Областью значений функции g(x)=2cos2x-2 является промежуток: в) [-2; 0] Областью значений функции t(x)=3cos2x-3 является промежуток: в) [-3; 0] График функции, изображенный на рисунке, задается формулой: в) y=-2sinx График функции, изображенный на рисунке, задается формулой: б) y=-0,5cosx Функция y=-cosx+1 возрастает на промежутках: а) [2 n; +2 n], n Z Функция y=sinx+1 убывает на промежутках: а) [ /2+2 n; 3 /2+2 n], n Z](https://fsd.videouroki.net/html/2017/12/02/v_5a22d49d44589/img8.jpg)
 g( /3) б) f( /3) /3) в) f( /3)=g( /3) Даны функции g(x)=sin2x cos4x и f(x)=cos2x sin4x. Если x=- /8, то а) g(- /8) /8) б) g(- /8)f(- /8) в) g(- /8)=f(- /8) Выражение тождественно равно: а) cos2α б) 1-sinα в) 1 Выражение тождественно равно: а) 1 б) sin2α в) 1-cosα " width="640"
g( /3) б) f( /3) /3) в) f( /3)=g( /3) Даны функции g(x)=sin2x cos4x и f(x)=cos2x sin4x. Если x=- /8, то а) g(- /8) /8) б) g(- /8)f(- /8) в) g(- /8)=f(- /8) Выражение тождественно равно: а) cos2α б) 1-sinα в) 1 Выражение тождественно равно: а) 1 б) sin2α в) 1-cosα " width="640"




 Получите свидетельство
Получите свидетельство Вход
Вход








 б)
б)  в)
в) 
 б)
б)  в)
в) 
 тождественно равно:
тождественно равно: тождественно равно:
тождественно равно: при
при  равно:
равно: при
при  равно:
равно:








 М-10 Свойства тригонометрических функций (266.85 KB)
М-10 Свойства тригонометрических функций (266.85 KB)
 0
0 1060
1060 24
24 Нравится
0
Нравится
0


