Логические элементы

Алгебра логики

Логические элементы

Логика - это наука о формах и способах мышления.

• Высказывание -это форма мышления, которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.
• Высказывание может быть истинно или ложно .

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения « истинно » и « ложно ».

Истинно =1

Ложно=0

Для образования новых высказываний используются базовые логические операции :

• логическое отрицание -операция не - инверсия
• логическое умножение - операция и - конъюнкция
• логическое сложение - операция или - дизъюнкция

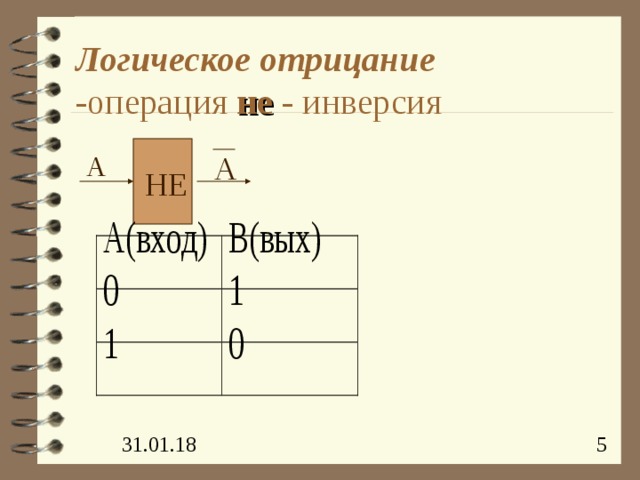
Логическое отрицание -операция не - инверсия

А

А

НЕ

Логическое умножение - операция и - конъюнкция

А

C=A&B

С

И

В

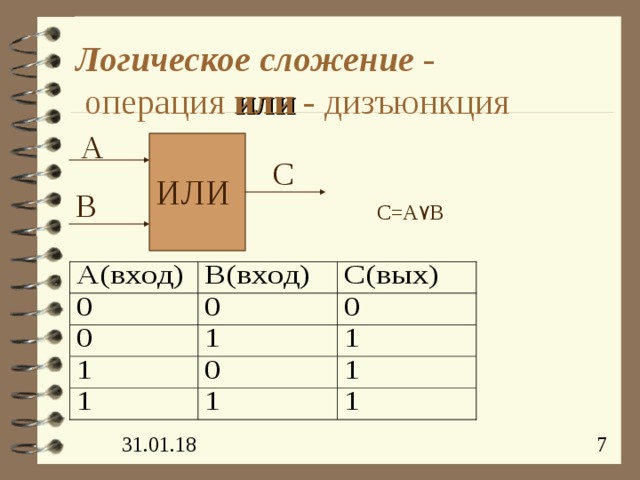
Логическое сложение - операция или - дизъюнкция

А

С

ИЛИ

В

C=A ۷ B

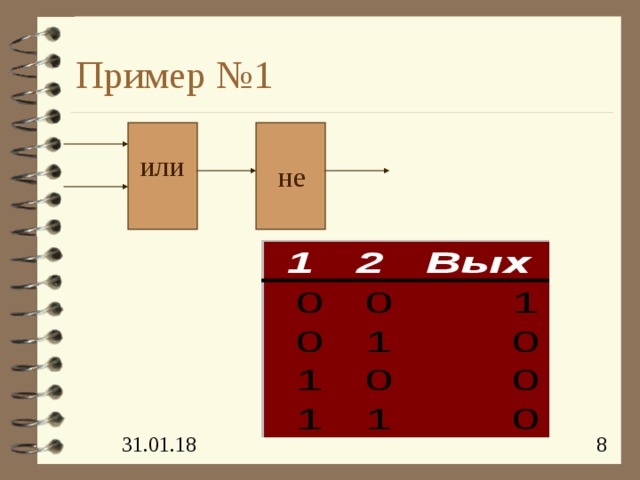
Пример №1

или

не

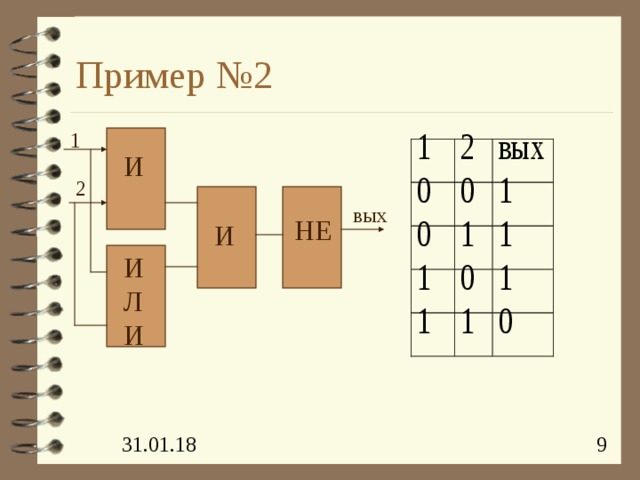
Пример №2

1

И

2

вых

НЕ

И

ИЛИ

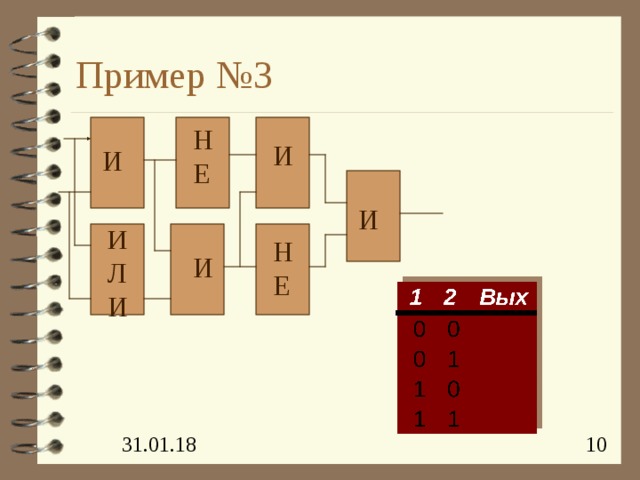
Пример №3

НЕ

И

И

И

И ЛИ

НЕ

И

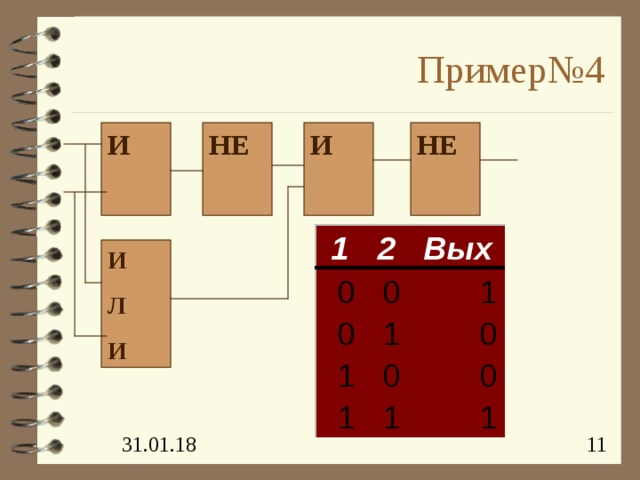
Пример№ 4

НЕ

НЕ

И

И

И

Л

И

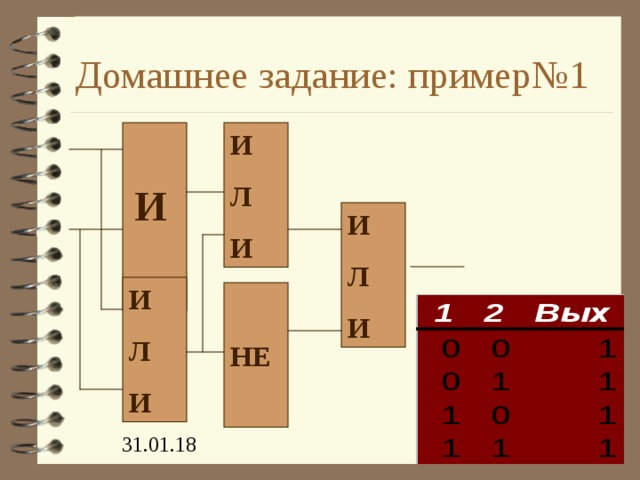
Домашнее задание: пример№1

И

И

Л

И

И

Л

И

И

Л

И

НЕ

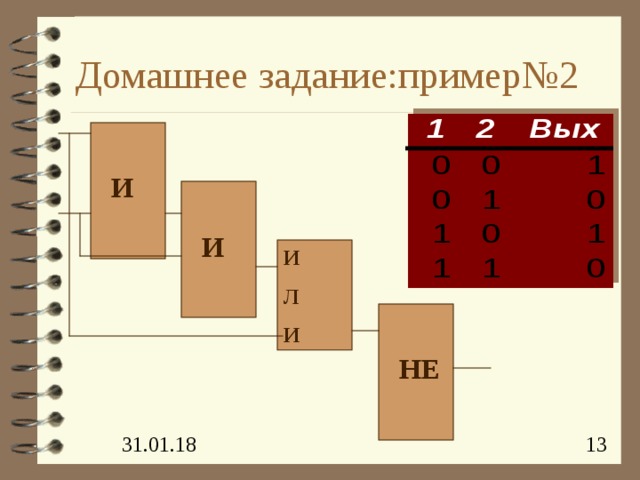
Домашнее задание:пример№2

И

И

И

Л

И

НЕ

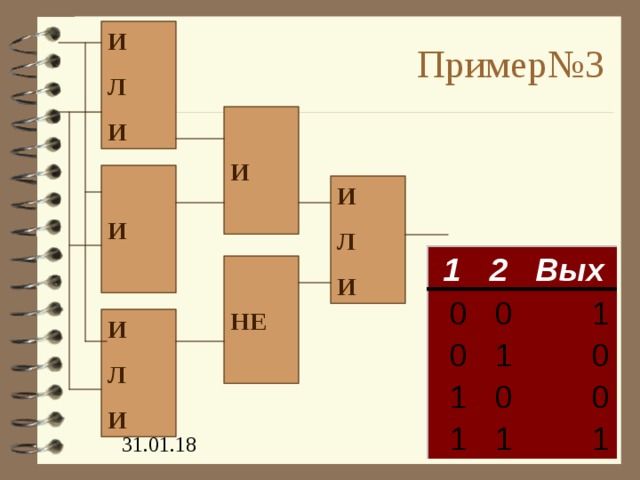
Пример№ 3

И

Л

И

И

И

И

Л

И

НЕ

И

Л

И

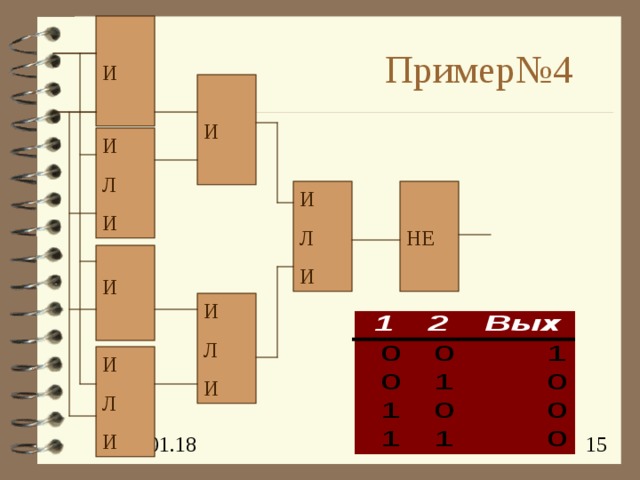
И

Пример№4

И

И

Л

И

НЕ

И

Л

И

И

И

Л

И

И

Л

И

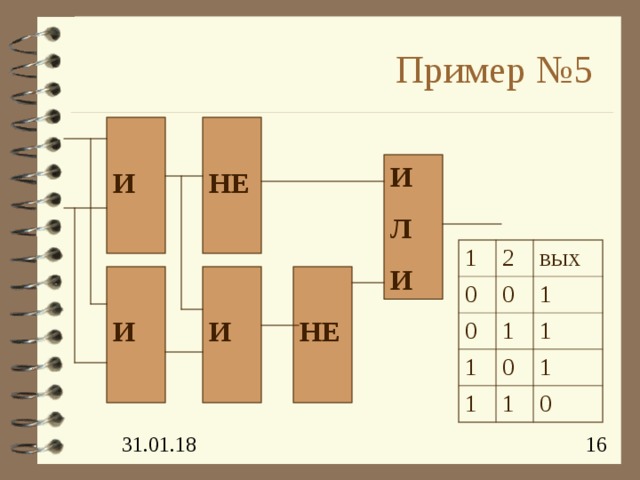
Пример № 5

И

НЕ

И

Л

И

1

0

2

0

0

вых

1

1

1

1

1

0

1

1

0

И

И

НЕ

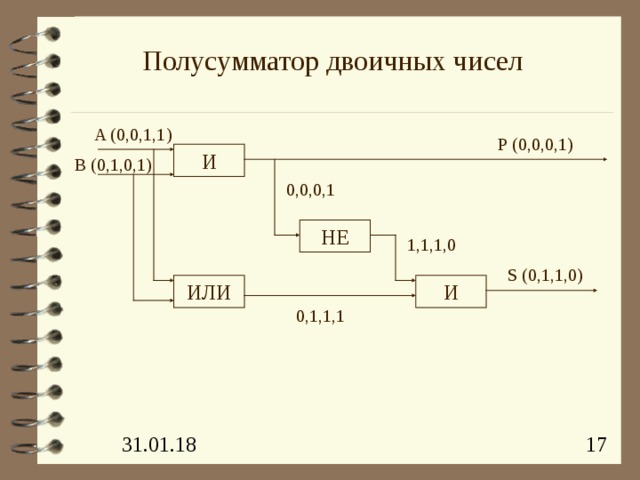
Полусумматор двоичных чисел

A (0,0,1,1)

Р (0,0,0,1)

И

B (0,1,0,1)

0,0,0,1

НЕ

1,1,1,0

S (0,1,1,0)

ИЛИ

И

0,1,1,1

Пример№ 6

F(A,B,C)=(A^B) ۷ (A ۷ C)

=(A*B)+(A+C)

Пример№ 6

F(A,B,C)=(A^B) ۷ (A ۷ C)

=(A*B)+(A+C)

۷ C

Пример№ 6

F(A,B,C)=(A^B) ۷ (A ۷ C)

=(A*B)+(A+C)

۷ C

Пример№ 6

F(A,B,C)=(A^B) ۷ (A ۷ C)

=(A*B)+(A+C)

۷ C

Пример№ 6

F(A,B,C)=(A^B) ۷ (A ۷ C)

=(A*B)+(A+C)

۷ C

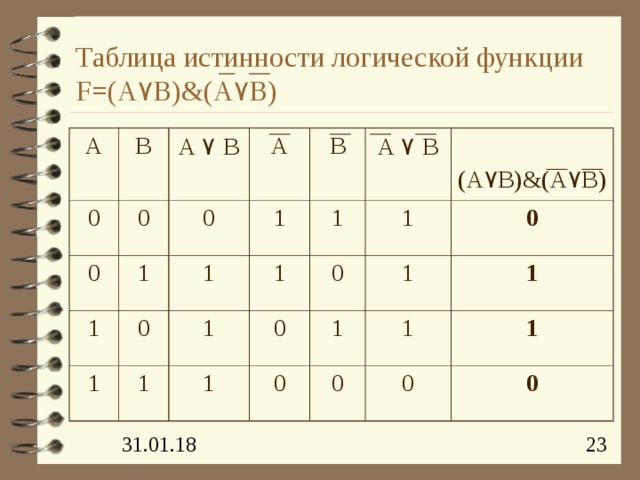
Таблица истинности логической функции F=(A ۷ B)&(A ۷ B)

A

B

0

0

0

A ۷ B

1

A

1

0

1

1

B

1

0

1

A ۷ B

1

1

1

1

(A ۷ B)&(A ۷ B)

0

0

1

0

1

1

0

1

0

1

0

1

0

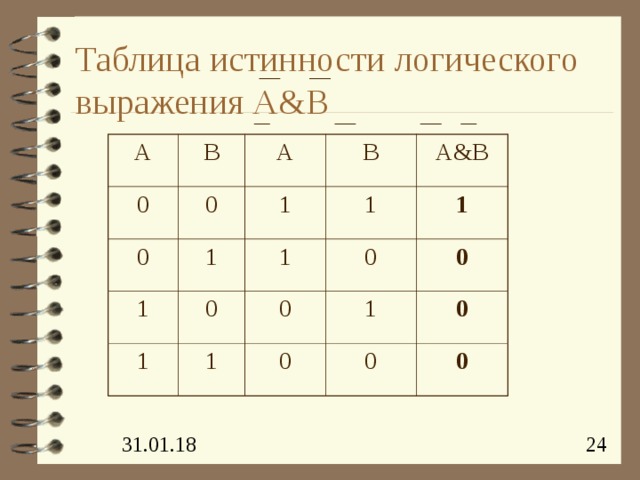
Таблица истинности логического выражения A&B

A

B

0

0

0

A

1

B

1

1

A&B

1

0

1

1

1

0

0

1

1

0

0

0

0

0

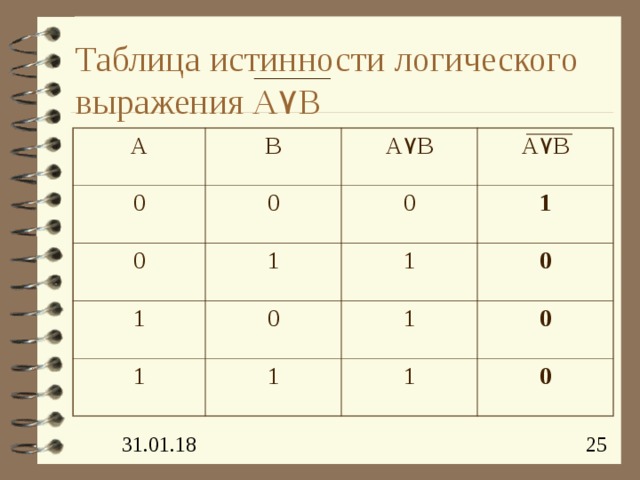
Таблица истинности логического выражения A ۷ B

A

B

0

0

0

A ۷ B

1

1

0

A ۷ B

1

0

1

1

1

1

0

0

1

0

Логические законы и правила преобразования логических выражений

• Закон тождества : всякое высказывание тождественно самому себе.

А=А

• Закон непротиворечия: высказывание не может быть одновременно истинным и ложным.

А & А=1

• Закон исключенного третьего. Высказывание может быть истинным, либо ложным, третьего не дано.

А ۷ А=1

• Закон двойного отрицания: если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.

А=А

Логические законы и правила преобразования логических выражений

• Законы Моргана:

А ۷ В=А & В

А & В=А ۷ В

• Таблицы истинности совпадают, следовательно, логические выражения равносильны: A&B = A&B
• Докажите , используя таблицы истинности, что логические выражения А ۷ В и А & В равносильны

Домашнее задание

• Докажите справедливость первого закона Моргана , используя таблицы истинности.
• Докажите справедливость второго закона Моргана , используя таблицы истинности.

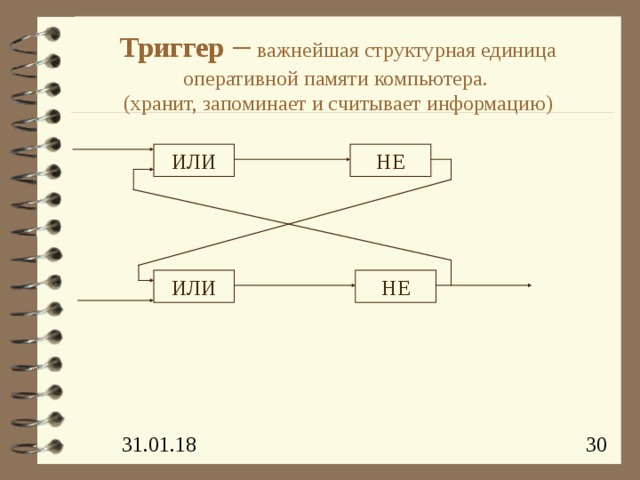
Триггер – важнейшая структурная единица оперативной памяти компьютера. (хранит, запоминает и считывает информацию)

ИЛИ

НЕ

НЕ

ИЛИ