Получите свидетельство
Вход
ԼՈԳԱՐԻԹՄԱԿԱՆ ՖՈՒՆԿՑԻԱ
Դասի նպատակները՝
Ի մանալ՝
լոգարիթմական ֆունկցիայի սահմանումն և հատկությունները
Կ արողանալ՝
Կ առուցել տարբեր հիմքերով լոգարիթմական ֆունկցիաների գրաֆիկներ, գրաֆիկների միջոցով համեմատել թվեր
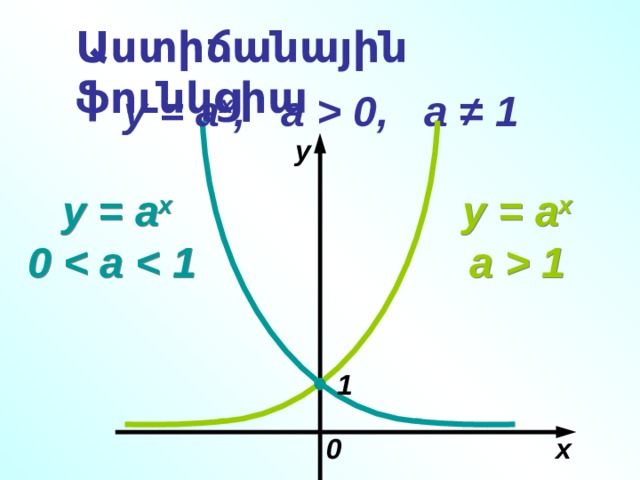0, a ≠ 1 y y = a x a 1 y = a x 0 1 x 0 " width="640"
Աստիճանային ֆունկցիա
y = a x , а 0, a ≠ 1
y
y = a x
a 1
y = a x
0
1
x
0
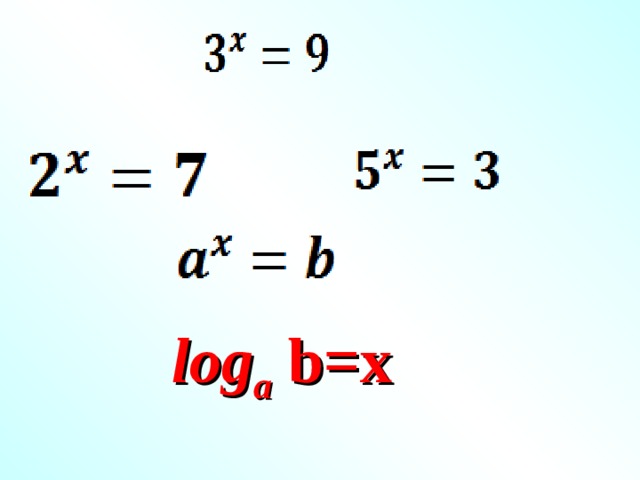
l og a b= x
ՋՈՆ ՆԵՊԵՐ (1550-1617)
- Շոտլանդացի մաթեմատիկ –
ստեղծել է լոգարիթմերը .
1590- ական թվականներին ստեղծեց լոգարիթմերը և կազմեց առաջին լոգարիթմական աղյուսակները, սակայն իր հռչակավոր
“ Լոգարիթմական զարմանալի աղյուսակների նկարագրությունը ” հրատարակեց միայն 1614 թվականին:
- Իրեն է պատկանում լոգարիթմերի սահմանումը, նրանց հատկությունների նկարագրությունը, սինուսների, կոսինուսների, տանգենսների լոգարիթմական աղյուսակները:
Լոգարիթմերի ստեղծումը, կրճատեց աստղագետի աշխատանքը և երկարացրեց նրա կյանքը
Պիեր Սիմոն Լապլաս
0, a 1 " width="640"
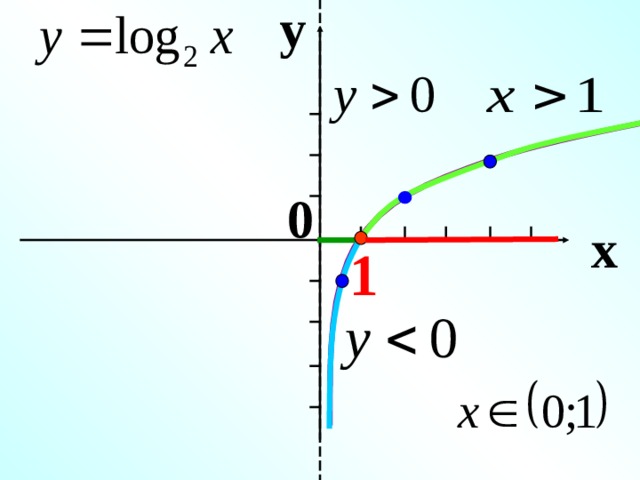
Լոգարիթմական ֆունկցիա
- Լոգարիթմական ֆունկցիա
- Լոգարիթմական ֆունկցիա
- Լոգարիթմական ֆունկցիա
- Լոգարիթմական ֆունկցիա
y = log a x
Որտեղ
a 0, a 1
0, a ≠ 1 1 о D(y)= (0 ; +∞) 2 о E(y)= ( − ∞; +∞) 3 о Ֆունկցիան ոչ կենտ է, ոչ զույգ 4 о եթե х = 1 , ապա у = 0 5 о եթե а 1 , ապա ֆունկցիան աճում է երբ х (0 ; +∞) եթե 0 а , ապա ֆունկցիան նվազում է при х (0 ; +∞) " width="640"
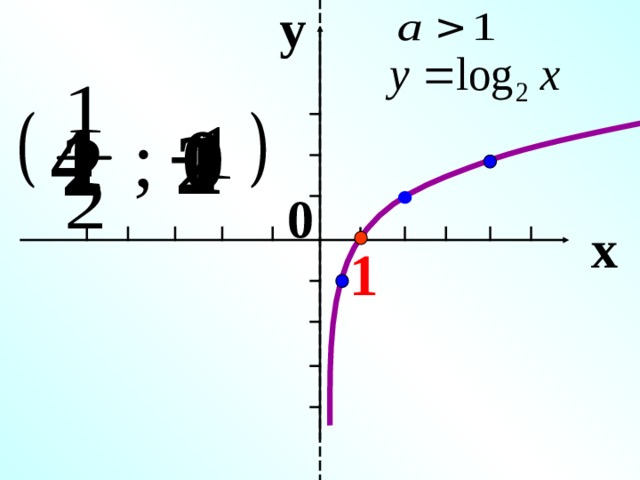
Լոգարիֆմական ֆունկցիայի հատկությունները y = log a x ,
а 0, a ≠ 1
1 о D(y)= (0 ; +∞)
2 о E(y)= ( − ∞; +∞)
3 о Ֆունկցիան ոչ կենտ է, ոչ զույգ
4 о եթե х = 1 , ապա у = 0
5 о եթե а 1 , ապա ֆունկցիան աճում է
երբ х (0 ; +∞)
եթե 0 а , ապա ֆունկցիան նվազում է
при х (0 ; +∞)
y
-1
1
4
0
2
1
2
0
x
1
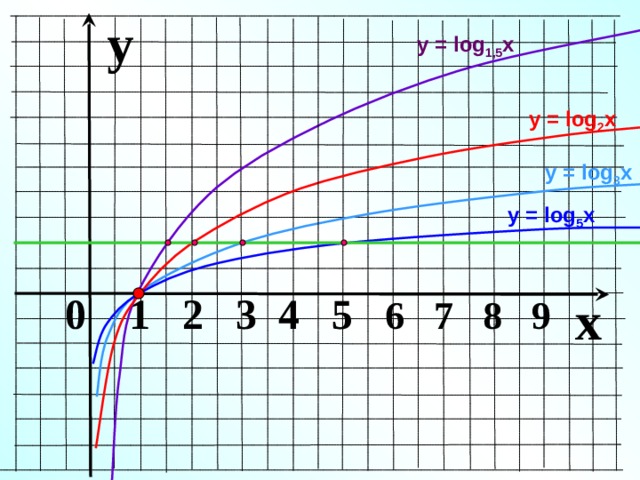
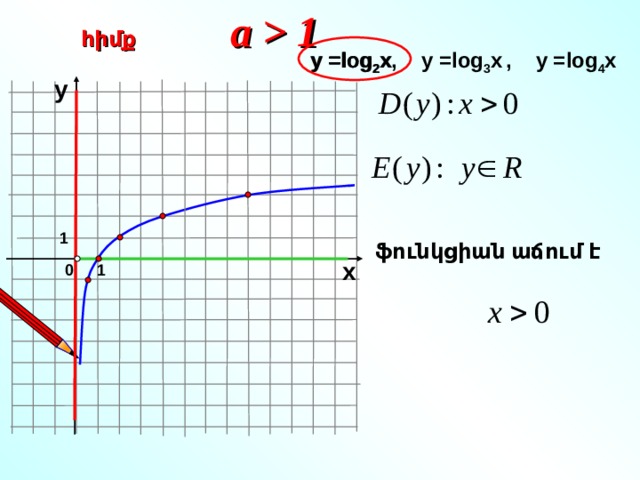1 հիմք у = log 2 x , у = log 3 x , у = log 4 x у = log 2 x у ֆունկցիան աճում է 1 х 0 1 " width="640"
a 1
հիմք
у = log 2 x , у = log 3 x , у = log 4 x
у = log 2 x
у
ֆունկցիան աճում է
1
х
0
1
y
0
x
1
y
у = log 1,5 x
у = log 2 x
у = log 3 x
у = log 5 x
x
0 1 2 3 4 5 6 7 8 9
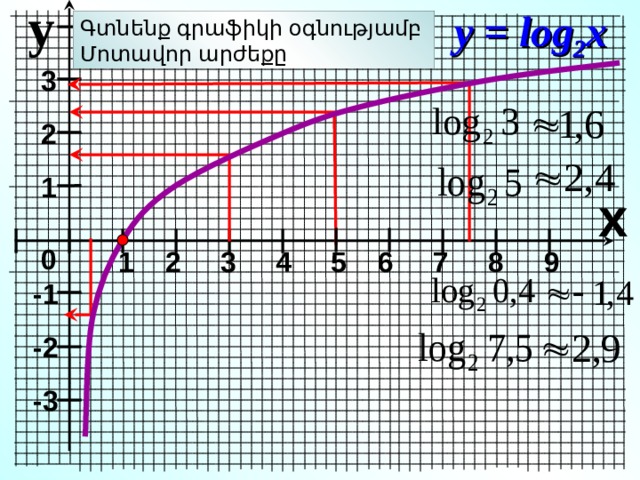
y
y = log 2 x
Գտնենք գրաֆիկի օգնությամբ
Մոտավոր արժեքը
3
2
1
0
-1
-2
-3
х
1 2 3 4 5 6 7 8 9
№ 323 . Найти приближенное значение.
12
y
0
1
0
1
-1
4
2
-2
0
1
x
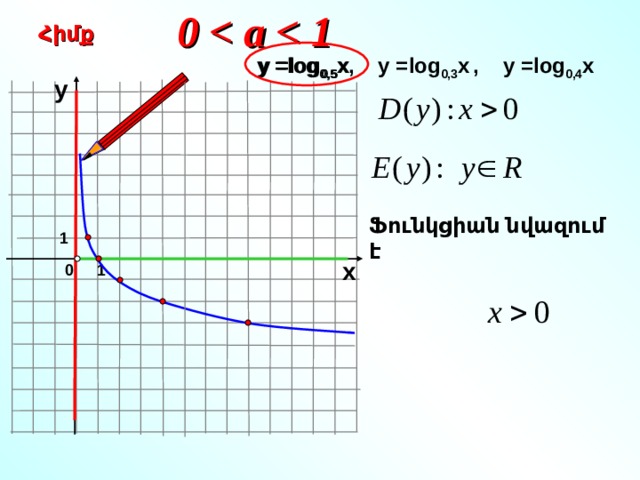
0 1
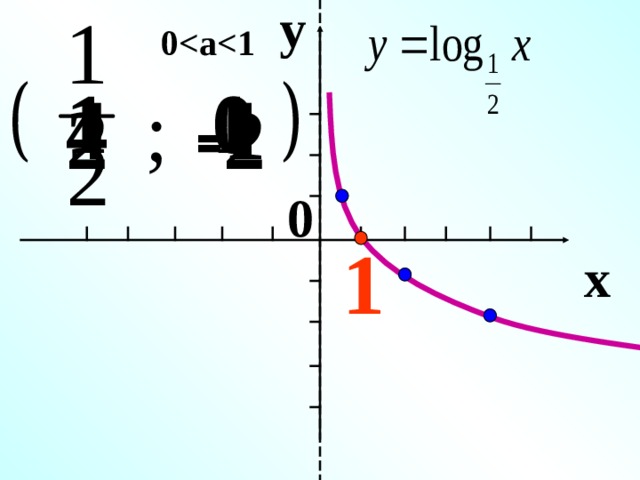
Հիմք
у = log 0,5 x
у = log 0,5 x , у = log 0,3 x , у = log 0,4 x
у
Ֆունկցիան նվազում է
1
х
1
0
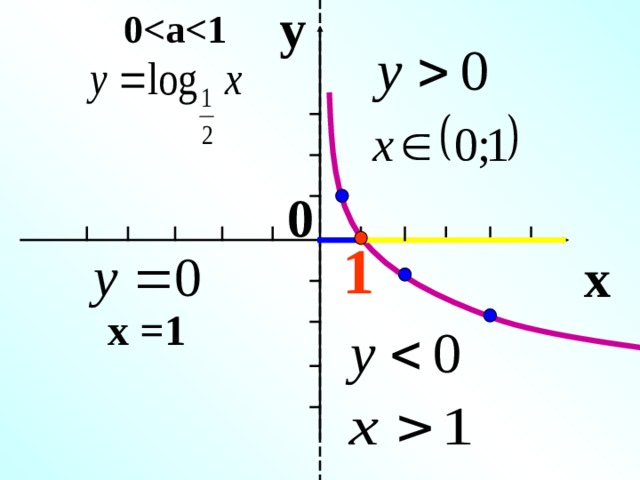
y
0
0
1
x
x =1
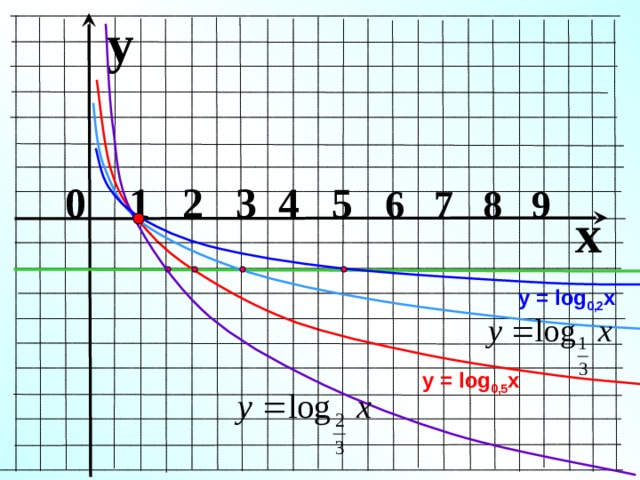
y
0 1 2 3 4 5 6 7 8 9
x
у = log 0,2 x
у = log 0,5 x
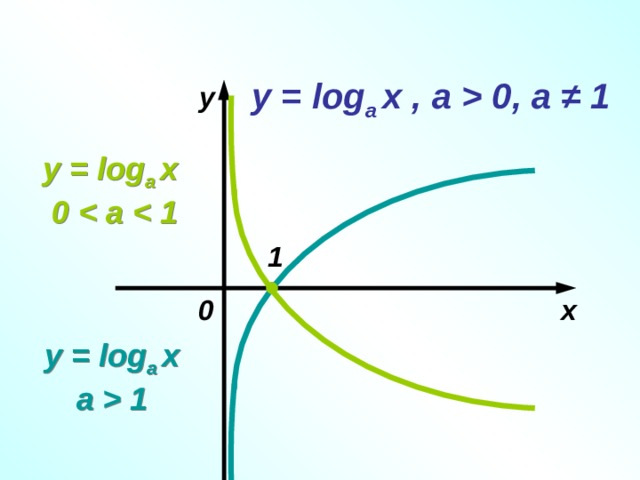0, a ≠ 1 y y = log a x 0 1 x 0 y = log a x a 1 " width="640"
y = log a x , а 0, a ≠ 1
y
y = log a x
0
1
x
0
y = log a x
a 1
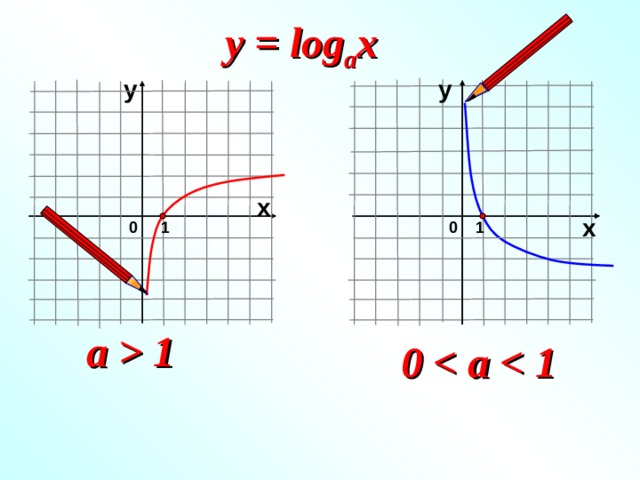1 0 1 19 " width="640"
y = log a x
у
у
х
х
1
1
0
0
a 1
0 1
19
0 у = log 2 x ֆունկցիան աճում է " width="640"
կարելի է համեմատել օգտագործելով աճման և նվազման հատկությունը
Թվերի համեմատում
log 3
log 3
2,7
4
Քանի որ у = log 3 x ֆունկցիան
աճում է
16
9
Քանի որ x ֆունկցիան
Ն վազում է
0
у = log 2 x ֆունկցիան աճում է
23 0 1 1 " width="640"
1
23
0
1
1
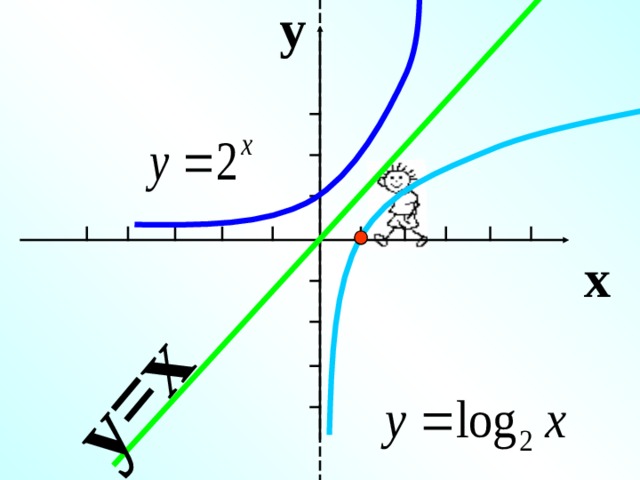
y
y=x
x
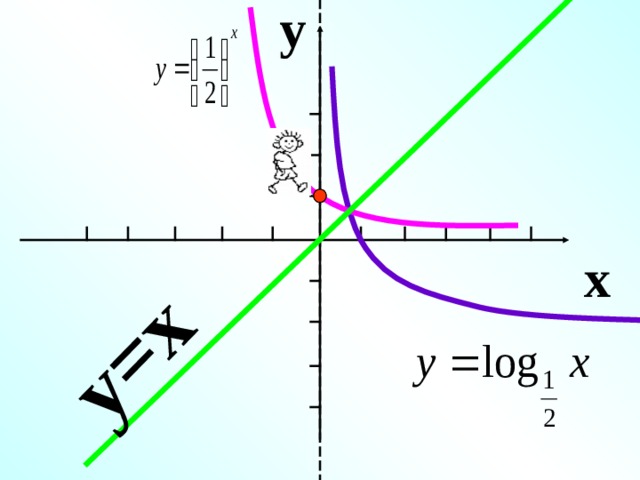
y
y=x
x
Մաթեմատիկայում հանդիպում են այսպես ասած էկզոտիկ գրաֆիկներ: Դրանցից մեկը լոգարիթմական սպիրալն է: Այն ունի ոլորաձև տեսք: Լոգարիթմական սպիրալը անվանում են նաև հավասար անկյուններ ունեցող սպիրալ: Սա ցույց է տալիս այն փաստը, որ լոգարիթմական սպիրալի ցանկացած կետում շոշափողի և շառավղի կազմած անկյունը հաստատուն է:
Հատկությունները
Կամայական ճառագայթ, որը դուրս է գալիս սպիրալի բևեռից, հատում է սպիրալի ցանկացած ոլորապտույտ նույն աստիճանի տակ;
Լոգարիթմական սպիրալը, ի տարբերություն շատ կորերի, ազդեծությունների դեպքում չի փոխում ի ր բնույթը: Ձգելով և լայնացնելով սպիրալը, մենք միայն փոխում ենք նրա անկյունը:
Մեկ այլ հատկություն
Եթե պտտենք սպիրալը բևեռի շուրջ ժամացույցի սլաքի ուղղությամբ, ապա թվում է թե սպիրալը ձգվում լայնանում է:
Լոգարիթմական սպիրալը բնության մեջ
Էպեյր սարդը հյուսում է իր սարդոստայնը լոգարիթմական սպիրալի տեսքով
Գիշատիչ թռչունները զոհի վրա պտտում են լոգարիթմական սպիրալի ձևով: Պարզվում է, որ նրանք ավելի լավ են տեսնում, երբ նայում են ոչ թե զոհի վրա, այլ մի փոքր կողք:
Շատ կենդանի օրգանիզմներ աճում են, երկարելով և լայնանալով:Սակայն ծովային կենդանիների կարող են աճել միայն մի ուղղությամբ, որպիսզի շատ չձգվեն, նրանք ոլորվում են: Իսկ այդպիսի ոլորապտույտը կարող է կատարվել միայն լոգարիթմական սպիրալի տեսքով: Բազմաթիվ կակղամորթերի , պարուրակների վահանակներ, ինչպես նաև կաթնասունների եղջյուրներ ունեն լոգարիթմական սպիրալի տեսք:
Մեծ գերմանացի բանաստեղծ Գյոթեն կարծում էր, որ լոգարիթմական սպիրալը, դա կյանքի և հոգևորի զարգացման մաթեմատիկական սիմվոլն է:
Արևածաղկի սերմերը նույնպես դասավորված են լոգարիթմական սպիրալի տեսքով:
Լոգարիթմական սպիրալի ձևով են դասավորված նաև շատ
գալակտիկաներ ,
այդ թվում նաև արեգակնային համակարգը
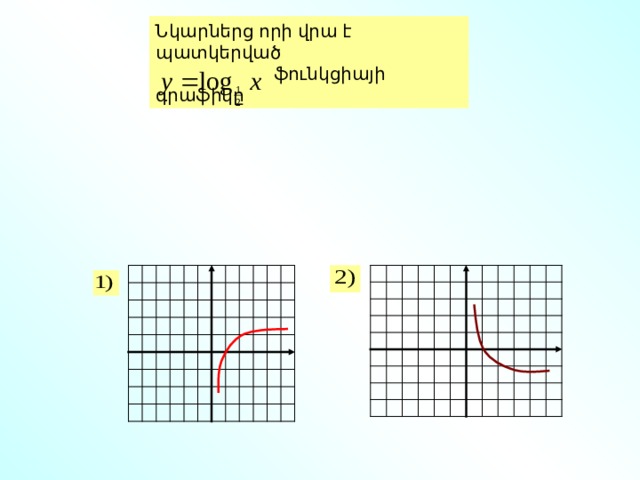
Նկարներց որի վրա է պատկերված
ֆունկցիայի գրաֆիկը
31
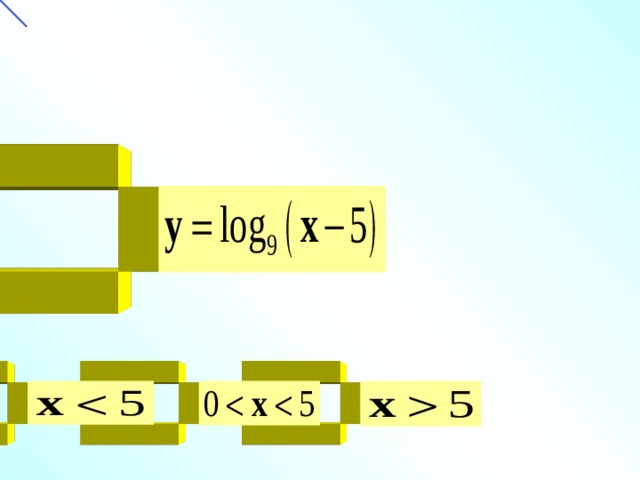
31
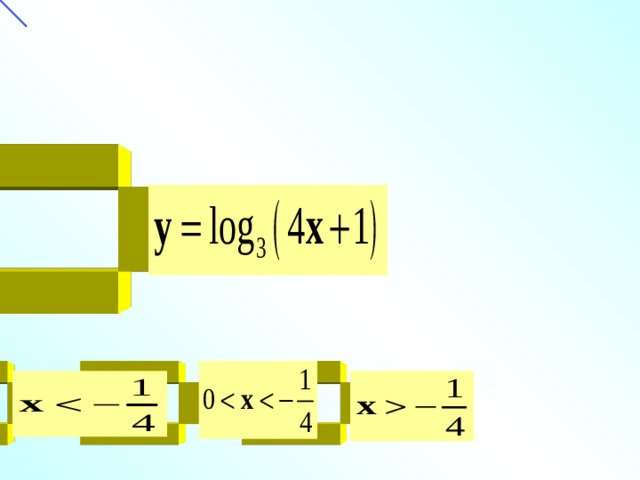
31
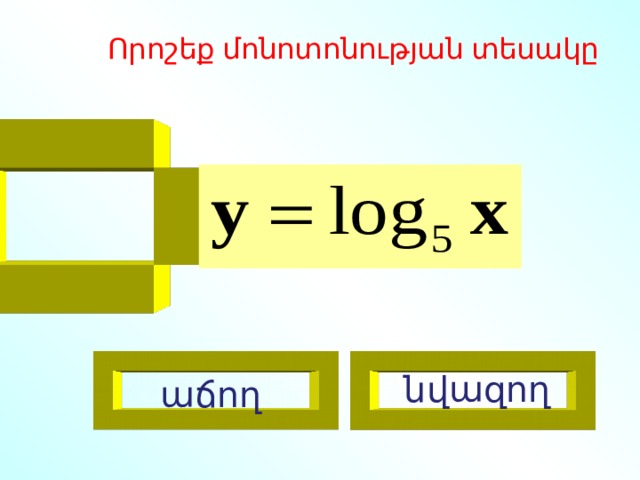
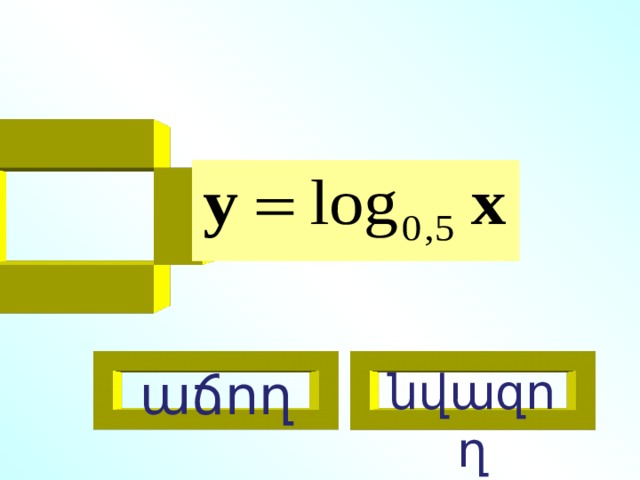
Որոշեք մոնոտոնության տեսակը
նվազող
աճող
31
աճող
նվազող
31
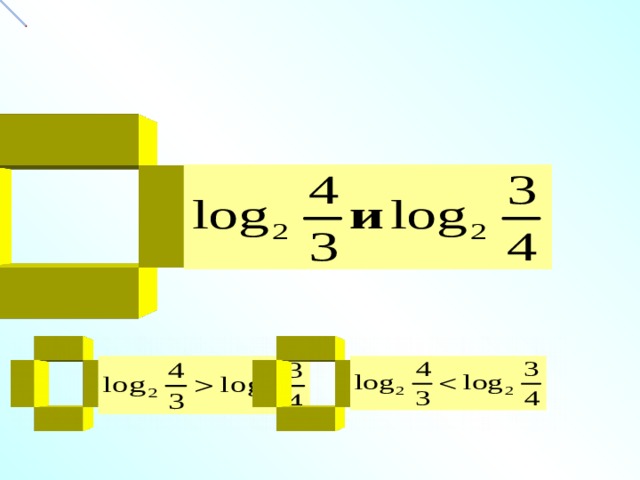
31
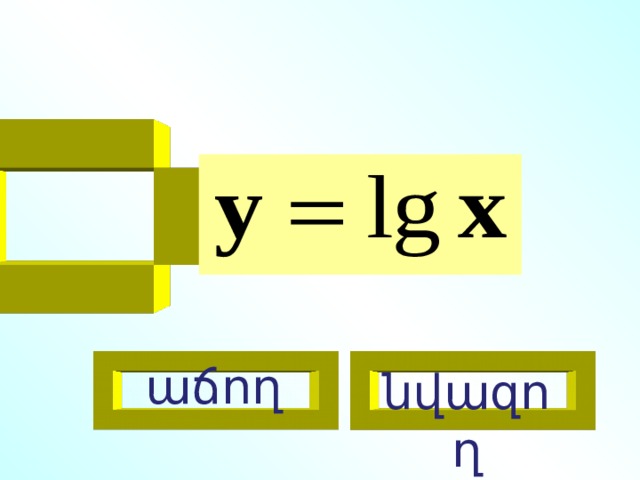
աճող
նվազող
31
Логаритмическая функция (1.74 MB)
0
43
2
Нравится
0
