Логарифмическая функция и ее свойства

КВАЛИФИКАЦИОННАЯ РАБОТА на тему : «Логарифмическая функция и ее свойства»

Слушатель курса “Математика”

Хаджибаева Ирина Ивановна

Ташкент, 2020 год

В презентации играет композиция «Музыка числа Пи»

2020 год –

Год развития науки, просвещения и цифровой экономики.

«Мы должны воспитать молодежь достойной наших великих предков, образованными и просвещенными личностями.»

Ш. М. Мирзиёев

Актуальность темы

• Логарифмическая функция нашла свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
• Так, изучение методов их решения логарифмических уравнений актуально и в дни современных технологий. Ведь вспомогательные устройства не всегда окажутся под рукой (экзамен, контрольная), поэтому необходимо привить учащимся знание хотя бы самых главных способов решения уравнений, неравенств и просто упрощений логарифмических выражений с применением всех свойств логарифмической функции. Тем самым развивая в учащихся умение мыслить самостоятельно.

Цель

• Помочь учащимся мыслить логически при сдаче вступительных экзаменов и тестов по математике, проверяющих умение учащихся оперировать такими понятиями, как система неравенств (пересечение множеств), совокупность неравенств (объедение множеств), осуществлять отбор решений неравенства, руководствуясь его областью допустимых значений .

• Объект исследования: система обучения математике учащихся к сдаче государственных экзаменов и тестов.

• Предмет исследования: методы решения различных логарифмических уравнений и неравенств, систем уравнений и понятие логарифмической функции с применением всех свойств логарифмической функции.

Основные тезисы

• Определение и свойства логарифма

• Методология решения логарифмических уравнений и неравенств

• Логаримическая функция. Её свойства и график

• Цели преподавателя в раскрытии темы и развитии учащихся

Определение логарифма и свойства логарифмов

• История появления логарифма

Основание понятия логарифма связано с несколькими именами: Михаил Штифель, Джон Непер и Иобст Бюрги .

Непер изначально назвал их «искусственными числами» , и лишь потом предложил слово «логарифм», в переводе с греческого «соотнесённые числа» .

Десятичные же логарифмы ввел ученый-математик Бригс , потому их иногда называют бригсовыми. Термин «характеристика» также ввёл Бригс.

Определение логарифма и свойства логарифмов

• Определение 1

Логарифмом положительного числа b по положительному и не равному единице основанию a называется показатель степени, в которую нужно возвести основание a , чтобы получить число b :

Определение логарифма и свойства логарифмов

Определение логарифма и свойства логарифмов

• Определение 2

Десятичным логарифмом называется логарифм по основанию десять:

Определение логарифма и свойства логарифмов

• Определение 3

Основанием натуральных логарифмов называется число e,

определенное замечательным пределом:

или производной

• Определение 4

Натуральным логарифмом называется логарифм по

основанию натуральных логарифмов: lnx = log e x

Методология решения логарифмических уравнений

• Логарифмическое уравнение (неравенство), содержит переменную под знаком логарифма и (или) в основании логарифма.

1. Методы решения простейшего логарифмического уравнения:

• потенционирование
• по определению логарифма

Методология решения логарифмических уравнений

2. Методы решения уравнения, содержащего суммы и разности логарифмов, умножение логарифма на число:

• применение свойств логарифмов

3. Методы решения уравнения вида: степени логарифма. Одно основание - одно выражение под логарифмом (либо одно основание - разные выражения под логарифмом):

• введение новой переменной и приведение к алгебраическим

Методология решения логарифмических уравнений

4. Методы решения уравнения вида: степени логарифма. Разные основания логарифмов:

• переход к логарифмам одного основания с использованием формулы перехода от логарифма одного основания к логарифмам другого

1 , то неравенство log a f(x) log a g(x) равносильно системе неравенств: Утверждение 2 Если 0 a , то неравенство log a f(x) log a g(x) равносильно системе неравенств: " width="640"

Методология решения логарифмических неравенств

• Утверждение 1

Если a 1 , то неравенство log a f(x) log a g(x) равносильно системе неравенств:

• Утверждение 2

Если 0 a , то неравенство log a f(x) log a g(x) равносильно системе неравенств:

log h(x) g(x) равносильно совокупности систем неравенств: * в неравенстве вместо знака может фигурировать любой из знаков ≥ , В этом случае утверждения 1-3 соответственно преобразуются. " width="640"

Методология решения логарифмических неравенств

• Утверждение 3

Неравенство log h(x) f(x) log h(x) g(x) равносильно совокупности систем неравенств:

* в неравенстве вместо знака может

фигурировать любой из знаков ≥ ,

В этом случае утверждения 1-3 соответственно преобразуются.

0, a не равно 1 " width="640"

Логарифмическая функция

Логарифмической функцией называется функция вида

у = log a x,

где а - заданное число, а 0, a не равно 1

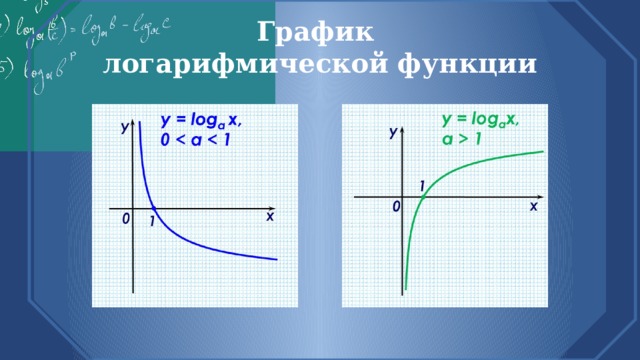
График логарифмической функции

0 . Свойство 2 Множеством значений логарифмической функции являются все действительные числа: E( y) = (− ∞ ; ∞ ) . " width="640"

Логарифмическая функция

• Свойство 1

Областью определения логарифмической функции являются все положительные действительные числа: D( y) = (0; ∞ ) .

Это следует из определения логарифма числа b по основанию а : log a b имеет смысл, если b 0 .

• Свойство 2

Множеством значений логарифмической функции являются все действительные числа: E( y) = (− ∞ ; ∞ ) .

Логарифмическая функция

• Свойство 3

Логарифмическая функция обращается в нуль при х = 1.

Решим уравнение: log a х = 0 .

По определению логарифма получаем: а 0 = х , т. е. х=1 .

1 . б) Логарифмическая функция у = log a х убывает на всей области определения, если 0 . " width="640"

Логарифмическая функция

• Свойство 4

а) Логарифмическая функция у = log a х возрастает на всей области определения, если а 1 .

б) Логарифмическая функция у = log a х убывает на всей области

определения, если 0 .

1 принимает положительные значения, если х 1 ; отрицательные значения, если 0 . б) при 0 принимает положительные значения, если 0 , и отрицательные значения. если х 1 . " width="640"

Логарифмическая функция

• Свойство 5

Логарифмическая функция у = log a х :

а) при а 1 принимает положительные значения, если х 1 ;

отрицательные значения, если 0 .

б) при 0 принимает положительные значения, если 0 , и отрицательные значения. если х 1 .

Выводы

Что нужно для того, чтобы решать логарифмические уравнения и неравенства? Какие качества нужно развить учащимся?

• внимание
• умение мыслить логически
• четкое знание свойств всех элементарных функций и понимание их смысла

Заключение

Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи.

Понятие логарифмов является неотъемлемой частью многих наук и деятельностей в повседневной жизни.

Логарифмы обладают важными свойствами , благодаря которым умножение можно заменить простым сложением, а извлечение корня и его возведение в степень можно преобразовать в умножение и в деление.

«...Методология должна быть такой, чтобы она пробуждала у детей любовь к математике. Учащиеся должны понимать, что эта наука нужна в жизни, в каждой сфере. Молодежь должна учиться не для того, чтобы сдать экзамен, а для того, чтобы стать образованными специалистами»

Ш. М. Мирзиёев

Спасибо за внимание!