Цель:
обобщить и систематизировать знания, умения и навыки по теме; развивать логическое мышление; воспитывать самостоятельность, любовь к математике.
Ход урока.
I Организационный момент.
II Проверка домашнего задания.
Учащиеся с высоким уровнем знаний выполняли нестандартные задания. Ребята демонстрируют решения своих задач.
1 задача. Требуется оградить прямоугольную площадку, примыкающую к стене. Забор должен иметь длину 60 м. Какой должна быть длина и ширина этой площадки, чтобы площадь ее была бы наибольшей?
2 задача. Испытывая судно, получили следующую таблицу зависимости между скоростью v (узлов) и мощностью h (лошадиных сил).
Предполагая, что зависимость между h и v есть квадратичная функция, найти мощность судна при скорости 6 узлов.
III Мотивация обучения.
Сегодня мы усовершенствуем умения решать неравенства методом интервала; строить графики функций с помощью простейших преобразований графиков функций; решать системы уравнений с двумя неизвестными.
Кроссворд с зашифрованным словом «Вавилон»
1. Наивысший показатель степени переменной в квадратном уравнение.
2. Выражение, с помощью которого определяют наличие и количество корней квадратного уравнения.
3. Квадратное уравнение, в котором коэффициент при (а=1).
4. Количество корней уравнения 2х-1=0.
5. График квадратичной функции.
6. Квадратное уравнение, в котором второй коэффициент или свободный член равен нулю.
7. Решение уравнения.

Исторические сведения.
Начало алгебры как науки про решение уравнений ученые нашли в египетских текстах. Но большой шаг вперед по сравнению с математиками Египта сделали ученые древнего Вавилона.
Именно они вывели правило для решения любого квадратного уравнения.
Способ решения квадратного уравнения вавилоняне предлагали в виде правила, в котором указывалось, какие действия и в какой последовательности нужно выполнять.
Если это правило перевести на современный язык, то получим формулу, которой пользуются и ныне.
IV Актуализация опорных знаний, навыков, умений.
Тестовые задания.
Каждый ученик получает карточку, в которой нужно указать выбранные ответы к заданиям.
V Применение обобщенных знаний, умений и навыков.
К доске вызываются 3 ученика. Каждому из них раздаются задания на карточках.
1. (х+1)(х-5)+6(х+1)<0
2. (х+2)2+14>18
3. у-2х2=2
3x+y=1
Каждое из решенных заданий проверяется учениками, сидящими за партами. Таким образом, учитель выставляет 6 оценок.
К доске вызываются ученики, которым предлагается выполнить следующее:
1. Построить график функции у=х2-2; у=(х+1)2 ; у=-х2
Эти задания выполняются на заранее приготовленной координатной плоскости и с помощью шаблона графика функции у=х2
2. Построить график функции у=2х2+3
VI Домашнее задание.
VII Итоги урока.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


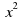 (а=1).
(а=1).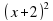 +1418
+1418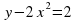
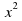 -2; у=
-2; у=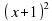 ; у=-
; у=-








 Квадратичная функция (конспект) (15.94 КB)
Квадратичная функция (конспект) (15.94 КB)
 0
0 1343
1343 188
188 Нравится
0
Нравится
0








