| Раздел долгосрочного плана:Квадратные корни и иррациональные выражения | Школа | |||||||||||||||||||||||||||||
| Дата: | ФИО учителя: | |||||||||||||||||||||||||||||
| Класс: | Количество присутствующих: | отсутствующих: | ||||||||||||||||||||||||||||
| Тема урока | Определения иррациональных и действительных чисел | |||||||||||||||||||||||||||||
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 8.1.1.1 усвоить понятия иррационального и действительного чисел;
| |||||||||||||||||||||||||||||
| Цели урока | - повторить определение натуральных, целых, рациональных чисел, изображение их с помощью кругов Венна - ввести понятие иррационального числа; - ввести понятие действительного числа ; | |||||||||||||||||||||||||||||
| Критерии оценивания | Учащийся достиг цели, если: - знает определение рациональных, иррациональных чисел и действительных чисел; - выбирает иррациональные числа из предложенных; - объясняет свой выбор во всех выполненных примерах; - определяет, какие числа получаются при сложении и умножении иррациональных чисел. | |||||||||||||||||||||||||||||
| Языковые цели | Учащиеся будут использовать математические термины в устной речи в рассуждениях о числах, основанные на понимании свойств иррациональных чисел Лексика и терминология, специфичная для предмета: Рациональное число, иррациональное число, целое число, дробь, знаменатель, десятичная дробь,иррациональное выражение, иррациональное число Полезные выражения для диалогов и письма: Иррациональные выражения являются … Иррациональные числа имеют десятичную дробь, которая не … Иррациональные числа и выражения, содержащие Является ли X/Y иррациональным числом? X должно быть иррациональным числом потому что … Yне может быть иррациональным числом потому что … Числа являются действительными … | |||||||||||||||||||||||||||||
| Привитие ценностей | Учащиеся будут развивать математическую речь, задания будут способствовать развитию критического мышления. | |||||||||||||||||||||||||||||
| Межпредметные связи |
| |||||||||||||||||||||||||||||
| Навыки использования ИКТ | Использование презентации при изучении нового материала, ссылки на видео обучающих уроков. | |||||||||||||||||||||||||||||
| Предварительные знания | Учащиеся знают про натуральные, целые, рациональные числа. | |||||||||||||||||||||||||||||
| Ход урока | ||||||||||||||||||||||||||||||
| Запланированные этапы урока | Запланированная деятельность на уроке | |||||||||||||||||||||||||||||
| Начало урока 10 минут
| Приветствие..Позитивный настрой на урок ( слайд2 ) Знакомство с темой урока, целями обучения и обсуждение критериев оценивания (слайд№3,4,5). Проверка домашнего задания | Презентация
| ||||||||||||||||||||||||||||
|
10 минут
15 минут
15 минут
20 минут
10 минут
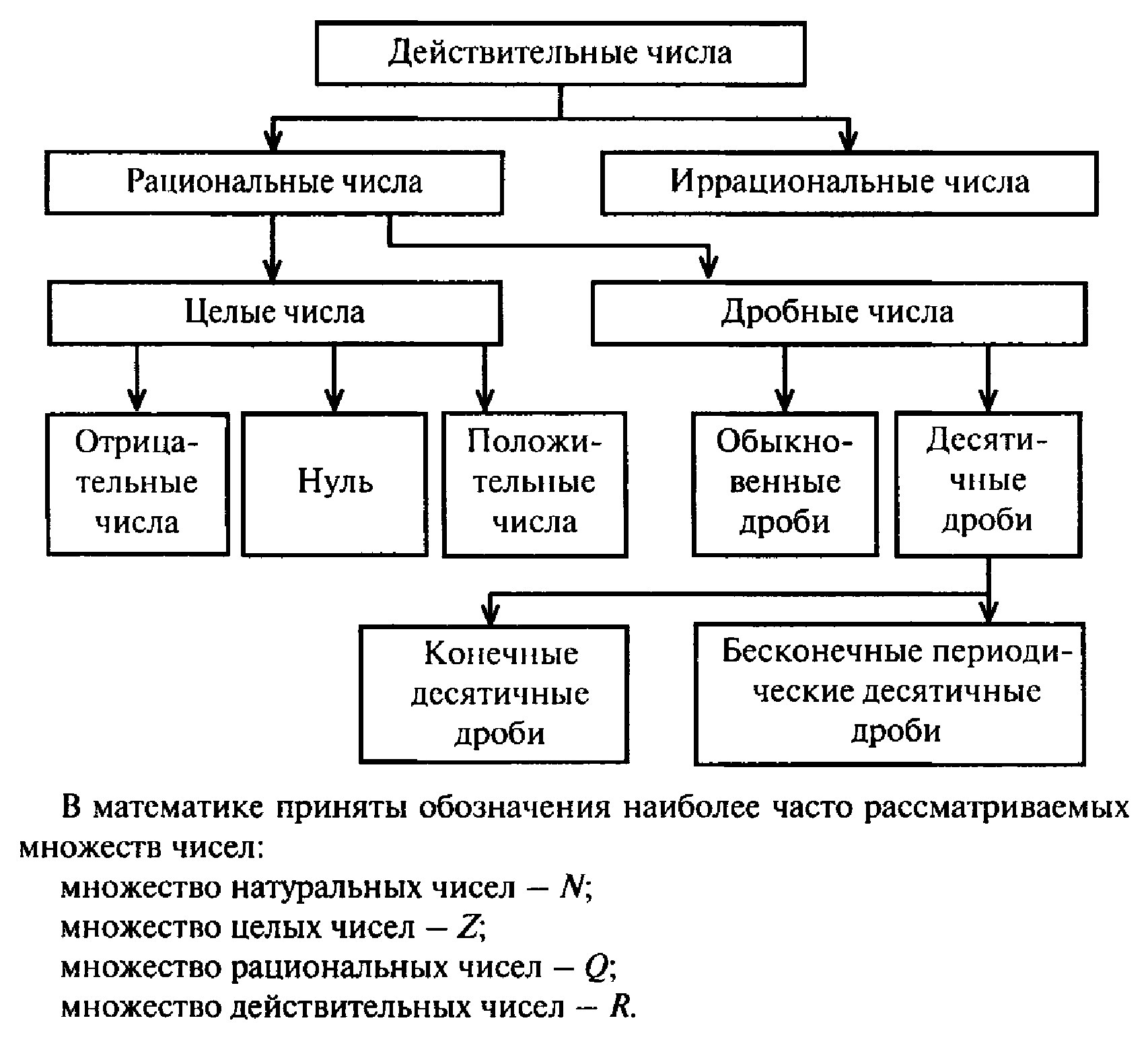
10 мин | 1.Повторение 1)Работа в парах. Задание: 1.Приведите три примера натуральных чисел. 2.Приведите три примера целых чисел. 3.Приведите три примера рациональных чисел. 4.Свериться с соседом по парте, обсудить. С помощью кругов Эйлера показать какие числа вы знаете: N ⊂ Z ⊂ Q . Q= { Множество рациональных чисел :множество несократимых дробей.Тогда запись будет такой: Q = { 2.Исследовательская деятельность, Работа в 4 группах по 3 человека. Задание: Выведем свойства множества Q.Привести пример и закончить предложение: При сложении рациональных чисел получается…. При вычитании рациональных чисел получается…. При умножении рациональных чисел получается…. При делении (не на 0) рациональных чисел получается…. При возведении в степень рационального числа получается… Каждая группа обосновывает одно утверждение. Остальные учащиеся слушают, имеют право добавлять, исправлять, выводы записывают в тетради. Вывод: Важной особенностью множества Q рациональных чисел является их замкнутость относительно операций: сложения; вычитания; умножения; деления (не на ноль); возведения в натуральную степень. В результате этих операций с рациональными числами мы снова получаем рациональное число. 3.Знакомятся с понятием иррационального числа Работа в парах . 1)Представьте в виде обыкновенной дроби число: а) 1,(3) б) 2,(25) в) 1,6(7) г) 0,41(6) д) 5,2(45) е) 3,4783694… Какой вывод можно сделать ? Число 3,4783694…невозможно представить в виде обыкновенной дроби , это число является иррациональным Определение : Иррациональным числом называется произвольная бесконечная непериодическая дробь. Иррациональное число нельзя представить в виде отношения Задание: Укажите, рациональное или иррациональное это число? -3,2 ; ; 1,2333… 5,13113111…; 0,1010010001…; -10,353535… -2,121121112…; 4. Определение действительных чисел Определение иррационального числа и понятие и обозначение действительного числа хорошо дано в видео BILIMLEND 1.учащиеся смотрят видео и делают записи в теради): http://bilimland.kz/ru/content/lesson/11287-irraczionalnye_chisla_mnozhestvo_dei_stvitelnyx_chisel «Определение множества действительных чисел» ( 1 минута) «Числовые множества»(1 минута) «Правило умножения иррациональных чисел»( 1 минута) 2.работа в парах Задание: Заполнить круги Венна. Свериться презентацией(слайд№6)
Множество рациональных и иррациональных чисел составляет множество действительных чисел 5.Работа в группах Тест Тrue/ False
6 Индивидуальное задание Тест с множественным выбором ответов | Приложение 1 Приложение 2 Презентация
Приложение 3
Презентация | ||||||||||||||||||||||||||||
| Конец урока 5 мин
| Рефлексия: Обсуждение вопросов: Что я нового узнал сегодня? Что понравилось в новой теме? Где данная тема пригодиться? Где возникли затруднения? Над чем надо поработать? Домашнее задание: |
| ||||||||||||||||||||||||||||
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | ||||||||||||||||||||||||||||
| Учащиеся будут работать и в индивидуальном режиме и в паре, и в группе. Более способные ученики смогут решить больше заданий. Однако следует призывать учащихся к ускорению темпа работы.
| Во время урока учитель будет оказывать поддержку учащимся. Учащиеся смогут самостоятельно оценивать свои работы, используя результаты ответов в процентах. | Кабинет будет проветрен, в классе будет обеспечена рабочая обстановка. | ||||||||||||||||||||||||||||
| Рефлексия по уроку
| Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. | |||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
Что могло бы способствовать улучшению урока (подумайте, как о преподавании, так и об обучении)?
Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
| ||||||||||||||||||||||||||||||

 Получите свидетельство
Получите свидетельство Вход
Вход


 ;
;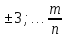 ,m
,m Z ,n
Z ,n ,m
,m









 КТП амыуппввпу цкупецуп (87.02 KB)
КТП амыуппввпу цкупецуп (87.02 KB)
 0
0 423
423 4
4 Нравится
0
Нравится
0



