
Линейная функция
и её график
Выполнила: учитель математики Сорокоумова Лена Семеновна
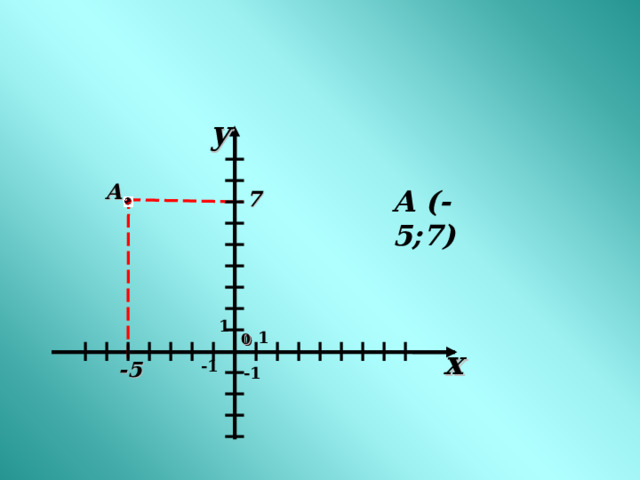
y
А
А (-5;7)
7
1
1
0
x
-5
-1
-1

у
А (2;3)
4
А
3
В (-1;-1)
D
2
D (-2;2)
1
x
Е (3;-2)
-4
-3
-2
-1
0
1
2
3
4
-1
В
E
-2
-3
-4
 0 y 0 x y 0 1 1 0 x III четверть IV четверть x 0 y x y " width="640"
0 y 0 x y 0 1 1 0 x III четверть IV четверть x 0 y x y " width="640"
y
I четверть
II четверть
x 0
y 0
x
y 0
1
1
0
x
III четверть
IV четверть
x 0
y
x
y

Способы задания функции:
- таблицей;
- формулой;
- графиком

у = kx
 0 k х " width="640"
0 k х " width="640"
у
k0
k
х

График функции у = kx проходит
через точку С (4;-8) . Найдите k .
k=-2

На каком рисунке изображён график линейной функции y = kx ? Ответ объяснить .
y
y
y
1 2 3
4 5
x
x
x
y
y
x
x

Задача 1.
Мама купила несколько конфет по цене 5 рублей за конфету и одну шоколадку по цене 65 рублей. Сколько она заплатила за всю покупку?
Составьте выражение, с помощью которого можно подсчитать стоимость покупки.
n - рублей стоит вся покупка
d – количество конфет
Как вы думаете, от чего зависит стоимость покупки?
n= 5 d +65
От числа покупаемых конфет.

Задача 2.
На шоссе расположены пункты А и В, удаленные друг от друга на 20 км.
Мотоциклист выехал из пункта В в направлении, противоположном А, со скоростью 50 км/ч. На каком расстоянии s (км) от пункта А будет мотоциклист через t часов?
От чего зависит расстояние от пункта А до мотоциклиста, если скорость и расстояние АВ постоянны? 50км/ч
А . . В
20км
От времени. Чем дольше едет мотоциклист, тем большее расстояние он проедет от пункта А.
 0. Обратите внимание на то, что полученная формула позволяет найти s для любого момента времени. " width="640"
0. Обратите внимание на то, что полученная формула позволяет найти s для любого момента времени. " width="640"
Какая формула выражает зависимость расстояния от времени движения? Давайте вспомним общую формулу, знакомую вам из курса физики Посмотрите на таблицу. Давайте разберемся, как получены значения расстояния.
s = vt .
В момент начала движения (t = 0) мотоциклист находился в пункте В, значит, s = 20 км. За 1 ч он отъехал от пункта В на 50 км, следовательно, расстояние s от пункта А до мотоциклиста s = 20 + 50 = 70 (км). За три часа мотоциклист отъехал от пункта В на расстояние, равное 150 км (используем формулу s=vt). Значит, расстояние от пункта А до мотоциклиста составит s = 20 + 150 = 170 (км).
Попробуйте записать формулу, выражающую зависимость расстояния от времени движения.
s = 50t + 20, где t 0.
Обратите внимание на то, что полученная формула позволяет найти s для любого момента времени.

Итак, мы получили две формулы, выражающие совершенно различные факты и явления, но имеющие одинаковую структуру:
n = 5d + 65
s = 50t + 20
Общий вид формулы: y = kx + b ,
где k и b – некоторые числа, x – переменная величина.
Можно предположить, что эти факты и явления описываются одной и той же формулой. Функция, с которой мы столкнулись в обеих задачах, называется линейной .

Определение
Линейной функцией называется функция, которую можно задать формулой вида у = k x + в, где
х – аргумент (независимая переменная)
k , b – числа, коэффициенты), к ≠ 0
у – функция (зависимая переменная)
k - угловой коэффициент прямой

Какие из данных функций являются линейными?

Проходит ли график функции
у = 3х-2 через точку А (5;13) ?
3*5 – 2 =13

Проходит ли график функции
у = -х + 6 через точку А (8;2) ?
-8 + 6 = -2
 0 b k0 k х " width="640"
0 b k0 k х " width="640"
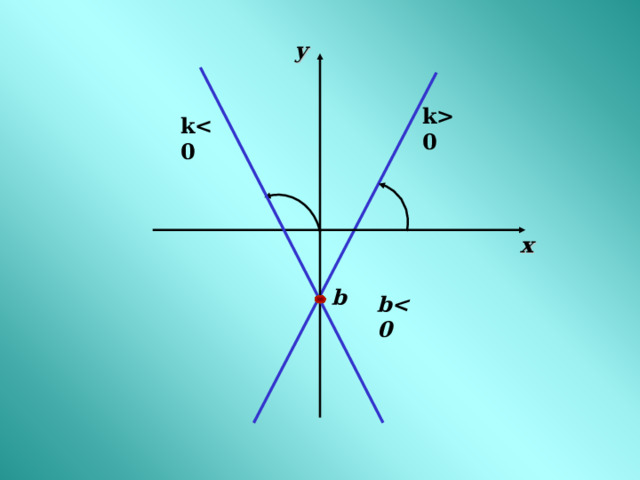
у
b0
b
k0
k
х
 0 k х b b " width="640"
0 k х b b " width="640"
у
k0
k
х
b
b

у = х + 2
у = -3х
у = 2х-2
у = -2х - 3

Выберите линейную функцию, график которой изображен на рисунке
у = 0,5х
у = х - 2
у = х – 1
у = х +2
у = х + 2
у = - х + 1
у = 2х
у = 2 – х
у = - х - 1
Молодец!
Подумай!
 0) Этой формулой задается прямая пропорциональность . Таким образом, прямая пропорциональность является частным случаем линейной функции. " width="640"
0) Этой формулой задается прямая пропорциональность . Таким образом, прямая пропорциональность является частным случаем линейной функции. " width="640"
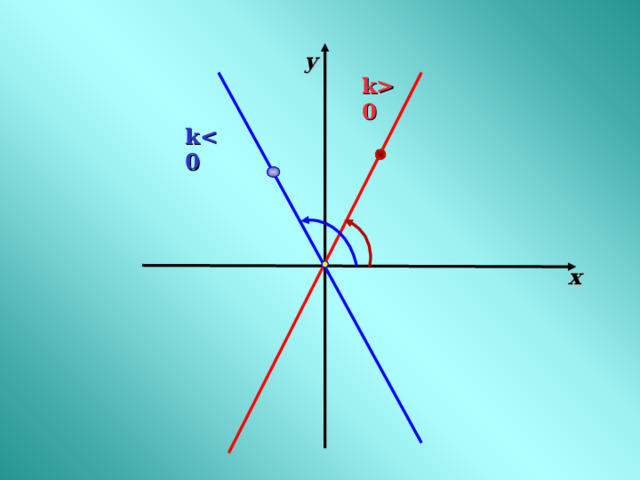
Рассмотрим частные случаи.
- Если b = 0 , то формула y = kx + b принимает вид y = kx ( k k 0)
Этой формулой задается прямая пропорциональность .
Таким образом, прямая пропорциональность является частным случаем линейной функции.
 0 k х " width="640"
0 k х " width="640"
у
k0
k
х

Рассмотрим частные случаи.
2) Если k = 0 , то формула y = kx + b принимает вид y = b .
Функция, задаваемая этой формулой, является линейной . Она принимает одно и то же значение при любом х .
 0 b 0 x " width="640"
0 b 0 x " width="640"
y
k=0
y=b, b0
b
0
x

y
0
x
b
k=0
y=b, b


-
-
-
-
-

Задать формулой функцию, график
которой параллелен прямой у = -8х + 11
и проходит через начало координат
- у = -8х + 1
- у = -8х
- у = 8х
- у = 11х

Является ли линейной функция
y = (5x –1) + (-8x +9) ?
Что бы ответить на этот вопрос нужно упростить правую часть выражения.
y = (5x –1) + (-8x +9)
у = 5 x - 1 - 8 x + 9
y = -3x + 8.
Ответ: функция линейная.
Выполните еще два аналогичных задания
у = 5х-10
у = -6х+46
I вар. y = 4(x – 3) + (x + 2)
II вар. у = 7(8 – x) + (x – 10)

Найти координаты точек пересечения графика у = 3х – 9 с осями координат.
1) Точка пересечения графика функции у = 3х – 9 с осью Ох находится из условия у = 0:
3х – 9=0, 3х=0+9, 3х=9, х=3.
(3;0)- точка пересечения графика функции у = 3х – 9 с осью Ох
2) Точка пересечения графика функции у = 3х – 9 с осью Оу находится из условия х = 0:
у = 3*0 – 9=-9
(0;-9)- точка пересечения графика функции у = 3х – 9 с осью Оу


Ученик допустил ошибку при построении графика функции. На каком рисунке?
1. y =х+2 2. y =1,5х 3. y =-х-1
y
y
y
3
3
2
x
1
x
x
1
3

На каком рисунке коэффициент k отрицателен?
y
1 2 3
4 5
y
y
x
x
x
y
y
x
x

На каком рисунке свободный член b в уравнении линейной функции отрицателен?
y
y
y
1 2 3
4 5
x
х
x
y
y
x
x

 Получите свидетельство
Получите свидетельство Вход
Вход











 Методическая разработка (2.96 MB)
Методическая разработка (2.96 MB)
 0
0 244
244 5
5 Нравится
0
Нравится
0



