| Дата: 9 Класс | ||||||
| Тема: Арифметическая прогрессия. Формула п-го члена арифметической прогрессии
| ||||||
| Цель урока: обеспечить повторение материалы темы, проверить усвоение определения арифметической прогрессии, знание формул п -членов арифметической прогрессии. Ожидаймый результат: содействовать развитию умения обобщить и систематизировать; содействовать проверке системы математических знаний, умений, навыков по теме »Арифметическая прогрессия», необходимых для общего образования, для практической деятельности в повседневной жизни. | ||||||
|
| Деятельность учителя | Деятельность обучающихся | наглядности | |||
| 3 мин | I. Организационный момент Приветствует учеников, делит класс на группы. Формулирует цель урока.
| Ученики делятся на группы. Осмысливают поставленную цель. | пазлы | |||
| 8 мин | II. Мотивация к изучению нового материала. Вызвать интерес учащихся к новому материалу.
А сейчас пока несколько ребят из группы будут выполнять тесты на компьютерах, мы с остальными поработаем устно. Компьютеры включены заранее, на рабочем месте лежит бумага и карандаш. Тесты выполняют:1.______________________ 2._____________________ 3.______________________ 4.______________________
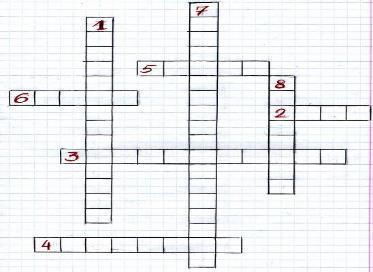
(хn): 3; 0; -3; -6; -9; -12;... назовите первый, третий и шестой члены. 2. Продолжите данную последовательность: 5; 9; 13; 17;… 3. Последовательность (аn) задана формулой аn = 6n - 1. Найдите: a1, а2, a3 ; а20, А сейчас в качестве небольшой разминки выполним кроссворд. Вопросы кроссворда: 1. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом. 2. Разность последовательно одинаковых членов. 3. Способ задания последовательности. 4. Разность последующего и предыдущего членов прогрессии. 5. Элементы, из которых состоит последовательность. 6. Натуральное число, обозначающее место члена в последовательности. 7. Функция, заданная на множестве натуральных чисел. 8. Последовательность, содержащая конечное число членов.
| Проявляют интерес к изучаемому материалу.
| карточки | |||
| 15 мин | III. Актуализация знаний. По методу «ДЖИГСО» научить учащихся свободно излагать свои мысли. Предлагает ученикам семантические карты. Ведут диалог друг с другом, выполняют творческое задание. Демонстрируют знания, умения. Учащиеся заполняют семантические карты. Семантические карты На доске последовательности : а) 5; 5; 5; 5; 5;…. б) 1; 0; 1; 0; 1; …. в) 3; 8; 15; 17; 31; …. г) 12; 15; 18; 21; 24; …. д) 6) Назовите какой номер в последовательности в) соответствует числу 15? (а3). 7) Как записать этот член? 8) Как записать следующий за ними член? (а4) 9) Как называется член последовательности, который стоит на n-м месте? (аn) 10) Как называется член последовательности, следующий за ним? 11) Как называется член последовательности, перед ним? Построение проекта выхода из затруднений. 26) Существует ли способ быстрого нахождения а45 ? - а2= а1 + d ; - а3 = а2 + d ( а по другому) = а1 + d + d =а1 + 2d - а4= а3 + d = а1 + 2d + d = а1 + 3d 27) Проанализируйте полученную закономерность. 28) Составьте формулу нахождения а45, учитывая полученную закономерность в предыдущей задаче. ( а45= а1 + 44d) 29) Обобщите результаты решения и запишите формулу нахождения п-го члена арифметической прогрессии ап.
аn= а1 + (n-1) d
30) Дополните тему нашего урока? (Формула n-го члена арифметической прогрессии). Задание для группы 1 группа 1. Известно, что а1 = 1, d = 2. Задайте эту прогрессию. 2. Выразите через а и d : а , а . 3. . Найдите а , если а = 4, d =7. (32) 4. Найдите а , если а = 20, а = 30. (25) 2 группа Найти сумму первых 24 членов арифметической прогрессии, заданной формулой Xn = 3n – 2 (852) Найдите разность арифметической прогрессии: В арифметической прогрессии (
3 группа . Найдите разность арифметической прогрессии, в которой у1 = 10; у5 = 22 Решение у доски: у5 = у1 + 4d Содержит ли арифметическая прогрессия 2; 9; … число 156 ? Решение у доски: аn = а1 + (n – 1) d Ответ: а23 = 156 4 группа . Найдите первые три члена арифметической прогрессии, в которой а1 + а5 = 24; Задание анализируем, составляем систему уравнений, которую предлагается решить дома. а1 + а1 + 4d = 24; Пусть (вn) - арифметическая прогрессия; 1) в1=11, d=3. Найдите в11. 2) в1=137, d= -7. Найдите S10 | |||||
| 8 мин | IV. Закрепление урока. По методу «Броуновское движение» осуществляет закрепление урока. Задание для группы Задания 1.
Задания 2.
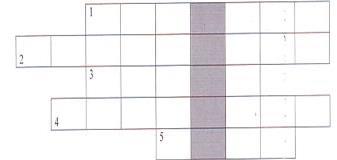
По горизонтали: 1. Последовательность можно задать с помощью... 2. Найдите второй член последовательности, заданной формулой ап =-2п2+58. 3. Найдите первый член арифметической прогрессии (сп ), если с3о=122, d=4. 4. В арифметической прогрессии d=an+1 ап называют... 5. Найдите пятый член арифметической прогрессии (вп),если Bi=19, d=-4,5. В вертикальном столбце выделите ключевое слово.
| Ученики обсуждают над темой. Таким образом демонстрируют свои знания, умения, навыки. | | |||
| 4 мин | V.Итог урока С помошью ромашки Блума формулирует выводы урока, контролирует выполнение записей учащимися, проводит рефлексию. -Какую цель мы поставили сегодня на уроке? -Достигли мы целей, которые ставили в начале урока? - Как вы оцените свою работу? | Фиксируют и анализируют выводы по уроку. Оценивают свою работу. | карточки стикер Дерево Блоба | |||
| 2 мин | YI. Домашнее задание. Объясняет особенности выполнения домашнего задания. | Записывают домашнее задание в дневники. | | |||

 Получите свидетельство
Получите свидетельство Вход
Вход



 ;
; 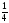 ;
;  ….
….
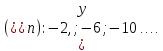
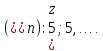
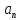 ) известны
) известны 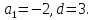 Найдите
Найдите 
 Я доволен собой, у меня все получилось.
Я доволен собой, у меня все получилось. У меня не все получилось, нужно повторить.
У меня не все получилось, нужно повторить. Многое не получилось, нужно повторить.
Многое не получилось, нужно повторить.








 КСП по алгебре "Арифметическая прогрессия. Формула n-го члена арифметической прогрессии" (68.37 KB)
КСП по алгебре "Арифметическая прогрессия. Формула n-го члена арифметической прогрессии" (68.37 KB)
 0
0 637
637 97
97 Нравится
0
Нравится
0


