Контрольная работа за 1 полугодие. 10 класс
Вариант 1
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный троичный код, позволяющий однозначно декодировать троичную последовательность, появляющуюся на приёмной стороне канала связи. Для букв А, Б, В и Г использовали такие кодовые слова: А–11, Б–12, В–21, Г–22. Укажите, каким кодовым словом может быть закодирована буква Д. Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.
1) 0 2) 01 3) 02 4) 10
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Какое выражение соответствует F?
1) x1¬x2x3¬x4x5x6¬x7
2) ¬x1x2¬x3x4¬x5¬x6x7
3) ¬x1x2¬x3x4x5x6x7
4) x1¬x2x3¬x4¬x5¬x6¬x7
Как записывается число 5678 в двоичной системе счисления?
1) 10111012 2) 1001101112 3) 1011101112 4) 111101112
Производится двухканальная (стерео) звукозапись с частотой дискретизации 8 кГц и глубиной кодирования 24 бит. Запись длится 4 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 11 2) 12 3) 13 4) 15
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке.Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
……
Запишите слово, которое стоит на 210-м месте от начала списка.
Для кодирования секретного сообщения используются 12 специальных значков-символов. При этом символы кодируются одним и тем же минимально возможным количеством бит. Чему равен информационный объем в байтах сообщения длиной в 256 символов?
Решите уравнение 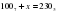 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
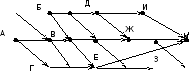
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 23

В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Пекин & (Москва | Токио) | 338 |
| Пекин & Москва | 204 |
| Пекин & Токио | 184 |
Сколько страниц (в тысячах) будет найдено по запросу Пекин & Москва & Токио
На числовой прямой даны два отрезка: P = [5, 15] и Q = [12, 18]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [3, 11] 2) [2, 21] 3) [10, 17] 4)[15, 20]
Вариант 2
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный троичный код, позволяющий однозначно декодировать полученную троичную последовательность. Вот этот код: А–0, Б–11, В–20, Г–21, Д–22. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.
1) для буквы Б – 1 2) это невозможно
3) для буквы В – 2 4) для буквы Д – 2Конец формы
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | F |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
Какое выражение может соответствовать F?
1) x1 x2 x3 ¬x4 ¬x5
2) ¬x1 x2 ¬x3 x4 ¬x5
3) x1 ¬x2 x3 ¬x4 x5
4) ¬x1 x2 x3 x4 ¬x5
Как записывается число 7548 в шестнадцатеричной системе счисления?
1) 73816 2) 1A416 3) 1EC16 4) A5616
Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 8 минут, ее результаты записываются в файл, сжатие данныхне производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в Мбайтах?
1) 30 2) 45 3) 75 4) 85
Все 5-буквенные слова, составленные из букв К, О, Р, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ККККК
2. ККККО
3. ККККР
4. КККОК
……
Запишите слово, которое стоит под номером 238.
В некоторой стране автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 12 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 32 автомобильных номеров.
Решите уравнение 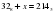 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?


В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество страниц (тыс.) |
| Попугай & (Антилопа | Тапир) | 340 |
| Попугай & Антилопа | 220 |
| Попугай & Тапир | 190 |
Сколько страниц (в тысячах) будет найдено по запросу Попугай & Антилопа & Тапир
На числовой прямой даны два отрезка: P = [5, 10] и Q = [15, 18]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [3, 11] 2) [6, 10] 3) [8, 16] 4)[17, 23]
Вариант 3
Для кодирования некоторой последовательности, состоящей из буквА, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи.Использовали код: А–111, Б–110, В–100, Г–101. Укажите, каким кодовым словом может быть закодирована буква Д.Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.
1) 0 2) 01 3) 00 4) 000
Дано логическое выражение, зависящее от 6 логических переменных:
X1¬X2X3¬X4X5X6
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 1 2) 2 3) 63 4) 64
Сколько значащих нулей в двоичной записи числа 254?
2) 2 3) 4 4) 8
4) Документ объемом 5 Мбайт можно передать с одного компьютера на другой двумя способами:
А) Сжать архиватором, передать архив по каналу связи, распаковать
Б) Передать по каналу связи без использования архиватора.
Какой способ быстрее и насколько, если
– средняя скорость передачи данных по каналу связи составляет 218 бит в секунду,
– объем сжатого архиватором документа равен 20% от исходного,
– время, требуемое на сжатие документа – 7 секунд, на распаковку – 1 секунда?
В ответе напишите букву А, если способ А быстрее или Б, если быстрее способ Б. Сразу после буквы напишите количество секунд, насколько один способ быстрее другого.
Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б23.
Слов «секунд», «сек.», «с.» к ответу добавлять не нужно.
Все 5-буквенные слова, составленные из букв И, О, У, записаны в алфавитном порядке и пронумерованы. Вот начало списка:
1. ИИИИИ
2. ИИИИО
3. ИИИИУ
4. ИИИОИ
……
Запишите слово, которое стоит под номером 240.
В велокроссе участвуют 678 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем в байтах сообщения, записанного устройством, после того как промежуточный финиш прошли 200 велосипедистов?
Решите уравнение 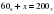 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?


Каким условием нужно воспользоваться для поиска в сети Интернет информации о цветах, растущих на острове Тайвань или Хонсю
1) цветы & (Тайвань | Хонсю)
2) цветы & Тайвань & Хонсю
3) цветы | Тайвань | Хонсю
4) цветы & (остров | Тайвань | Хонсю)
На числовой прямой даны два отрезка: P = [6, 16] и Q = [30, 50]. Отрезок A таков, что формула
( (x Î А) → (x Î Q) ) \/ (x Î P)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?
1) 10 2) 20 3) 21 4)30
Вариант 4
Для кодирования некоторой последовательности, состоящей из букв А, Б, В,Г и Д, используется неравномерный двоичный код, позволяющий однозначнодекодировать полученную двоичную последовательность. Вот этот код:А – 00, Б – 01, В – 100, Г – 101, Д – 110. Можно ли сократить для одной избукв длину кодового слова так, чтобы код по-прежнему можно былодекодировать однозначно? Коды остальных букв меняться не должны.
Выберите правильный вариант ответа.
1) это невозможно
2) для буквы Г – 10
3) для буквы Д – 11
4) для буквы Д – 10
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Какое выражение соответствует F?
1) x1→(x2x3x4x5x6x7)
2) x2→(x1x3x4x5x6x7)
3) x3→(x1x2x4x5x6x7)
4) x4→(x1x2x3x5x6x7)
Сколько единиц в двоичной записи числа 173?
1)4 2) 5 3) 6 4) 7
В течение трёх минут производилась четырёхканальная (квадро) звукозапись с частотой дискретизации 16 кГц и 24-битным разрешением. Сжатие данных не производилось. Какая из приведённых ниже величин наиболее близка к размеру полученного файла?
1) 25 Мбайт 2) 35 Мбайт 3) 45 Мбайт 4) 55 Мбайт
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке.Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
……
Запишите слово, которое стоит на 125-м месте от начала списка.
В базе данных хранятся записи, содержащие информацию о датах. Каждая запись содержит три поля: год (число от 1 до 2100), номер месяца (число от 1 до 12) и номер дня в месяце (число от 1 до 31). Каждое поле записывается отдельно от других полей с помощью минимально возможного числа бит. Определите минимальное количество бит, необходимых для кодирования одной записи.
Решите уравнение 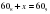 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?

Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
| Ключевое слово | Количество сайтов, для которых данное слово является ключевым |
| сомики | 250 |
| меченосцы | 200 |
| гуппи | 500 |
Сколько сайтов будет найдено по запросу сомики | меченосцы | гуппи
если по запросу сомики & гуппи было найдено 0 сайтов,
по запросу сомики & меченосцы – 20,
а по запросу меченосцы & гуппи – 10.
10) На числовой прямой даны два отрезка: P = [10, 40] и Q = [30, 50]. Отрезок A таков, что формула ( (x А) → (x Q) ) \/ (x P) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?
1) 10 2) 20 3) 30 4)40
Ответы к контрольной работе за 1 полугодие
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вариант 1 | 1 | 2 | 3 | 1 | УОУАУ | 128 | 24 | 23 | 50 | 3 |
| Вариант 2 | 1 | 4 | 3 | 1 | РРРОК | 128 | 53 | 14 | 70 | 2 |
| Вариант 3 | 1 | 3 | 1 | А120 | УУУОУ | 250 | 2 | 20 | 1 | 2 |
| Вариант 4 | 3 | 4 | 2 | 2 | ОООУО | 21 | 10 | 9 | 920 | 4 |
Критерии оценивания:
9 -10 верно выполненных заданий – оценка «5»;
7-8 верно выполненных заданий – оценка «4»;
5-6 верно выполненных заданий – оценка «3»;
менее 5 верно выполненных заданий – оценка «2»;


 Получите свидетельство
Получите свидетельство Вход
Вход


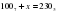 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.

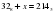 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
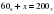 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
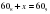 . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.
. Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.









 Контрольная работа по информатике за 1 полугодие (0.11 MB)
Контрольная работа по информатике за 1 полугодие (0.11 MB)
 0
0 9317
9317 1190
1190 Нравится
0
Нравится
0





