Контрольная работа. Теория графов

Контрольная работа. Теория графов

Вариант 1

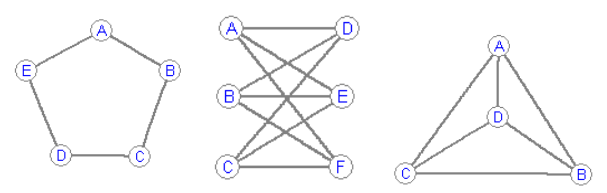
Задание 1. Раскрасьте вершины графа в минимальное количество цветов так, чтобы смежные вершины получали бы разные цвета. Для каждого графа укажите минимальное количество используемых цветов.

Задание 2. В стране Озёрная 7 озер, соединенных между собой 10 непересекающимися каналами, причём от каждого озера можно доплыть до любого другого. Сколько в этой стране островов? Нарисуйте получившийся граф.

Задание 3. Ориентированный граф G c множеством вершин V = {1, 2, 3, 4, 5, 6} задан списком дуг {(1, 6), (2, 1), (2, 5), (3, 1), (3, 3), (3, 5), (3, 2), (3, 6), (5, 1), (5, 6), (6, 4), (6, 5)}. Построить реализацию графа.

Задание 4. Опишите граф с помощью матрицы смежности. Постройте матрицу инцидентности.

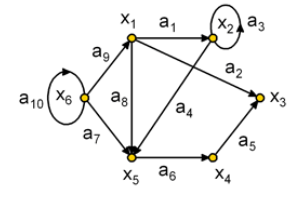
Задание 5. Подпишите типы и виды графов, укажите на примере одного графа вершину, начальную вершину, конечную вершину, дугу, ребро, петлю.

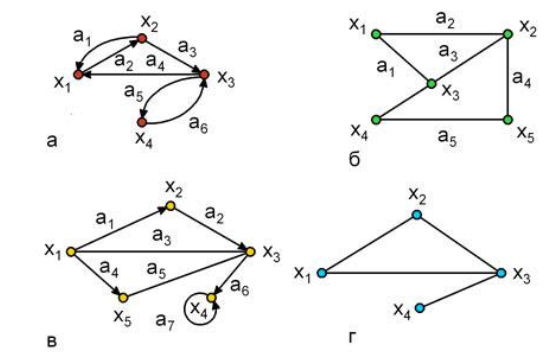
Задание 6. Дан граф. Укажите для него маршрут, путь, цикл. Для указанного маршрута обозначьте вершины, ребра, длину:

Задание 7.Заполните схему:

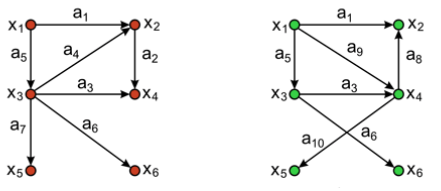
Задание 8. Выполните операцию объединения графов (нарисуйте результирующий граф):

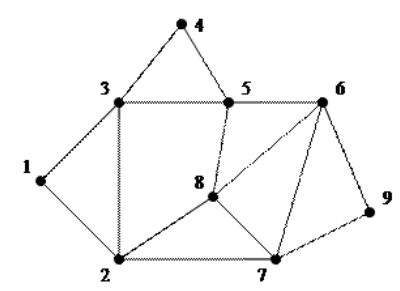
Задание 9. Найдите в данном графе эйлеров и гамильтонов цикл:

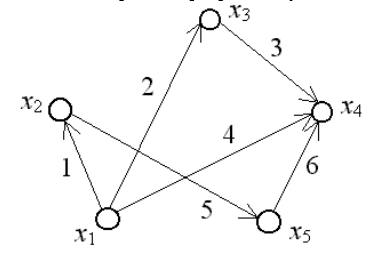
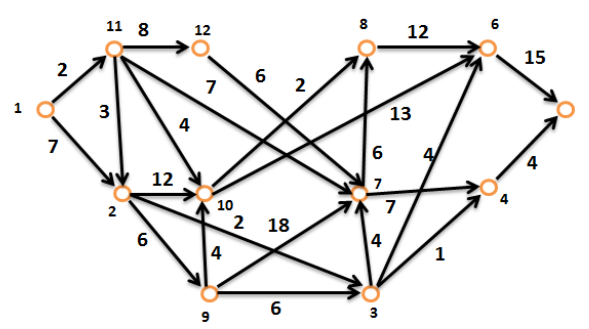
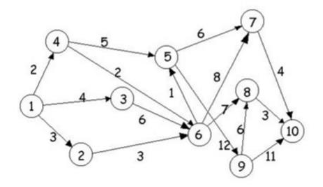
Задание 10. Найти все пути из 1 в 7 в графе G=(Х,Г) изображенном на рисунке 1.

Задание 11. Найдите минимальное остовное дерево с помощью алгоритма Краскала. Запишите алгоритм построения.

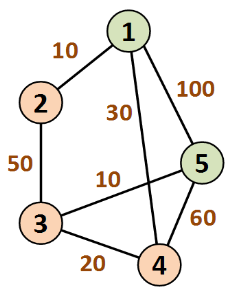
Задание 12. Дан граф. Найдите кратчайший путь из вершины 1 в вершину 5 используя алгоритм Дейкстры. Записать по шагам работу алгоритма.

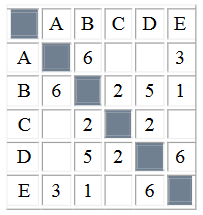
Задание 13. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице. Постройте граф. Определите длину кратчайшего пути между пунктами A и D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Запишите название и работу по шагам используемого алгоритма.

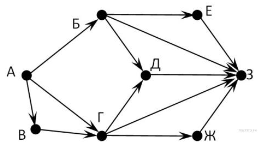
Задание 14. На рисунке –схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?

Контрольная работа. Теория графов

Вариант 2

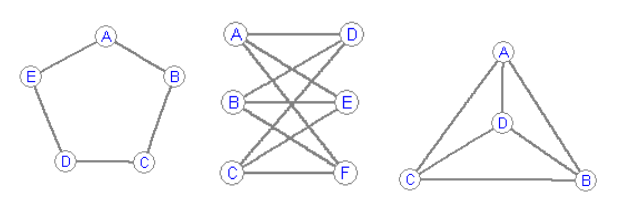
Задание 1. Раскрасьте ребра графа в минимальное количество цветов так, чтобы смежные ребра получали бы разные цвета. Для каждого графа укажите минимальное количество используемых цветов.

Задание 2. В стране Озёрная 7 озер, соединенных между собой 10 непересекающимися каналами, причём от каждого озера можно доплыть до любого другого. Сколько в этой стране островов? Нарисуйте получившийся граф.

Задание 3. Ориентированный граф G c множеством вершин V = {1, 2, 3, 4, 5, 6} задан списком дуг {(1, 6), (2, 1), (2, 3), (3, 1), (3, 3), (3, 3), (3, 4), (3, 6), (5, 1), (5, 6), (5, 6), (5, 6), (6, 4), (6, 6)}. Построить реализацию графа.

Задание 4. Опишите граф с помощью матрицы смежности. Постройте матрицу инцидентности.

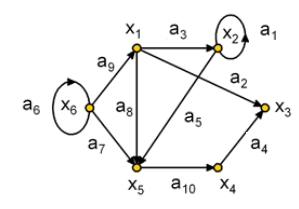
Задание 5. Подпишите типы и виды графов, укажите на примере одного графа вершину, начальную вершину, конечную вершину, дугу, ребро, петлю.

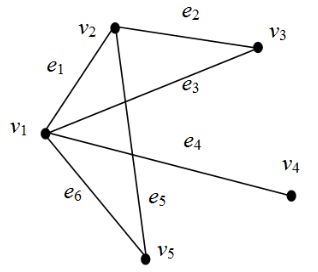
Задание 6. Дан граф. Укажите для него маршрут, путь, цикл. Для указанного маршрута обозначьте вершины, ребра, длину:

Задание 7.Заполните схему:

Задание 8. Выполните операцию объединения графов (нарисуйте результирующий граф):

Задание 9. Найдите в данном графе эйлеров и гамильтонов цикл:

Задание 10. Найти все пути из 1 в 7 в графе G=(Х,Г) изображенном на рисунке 1.

Задание 11. Найдите минимальное остовное дерево с помощью алгоритма Краскала. Запишите алгоритм построения.

Задание 12. Дан граф. Найдите кратчайший путь из вершины 1 в вершину 5 используя алгоритм Дейкстры. Записать по шагам работу алгоритма.

Задание 13. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице. Постройте граф. Определите длину кратчайшего пути между пунктами A и D. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Запишите название и работу по шагам используемого алгоритма.

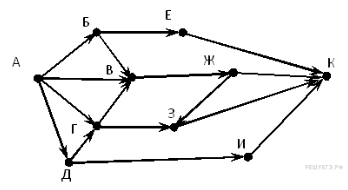
Задание 14. На рисунке—схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей изгорода А в город К?

Задание 15. Выполните тест

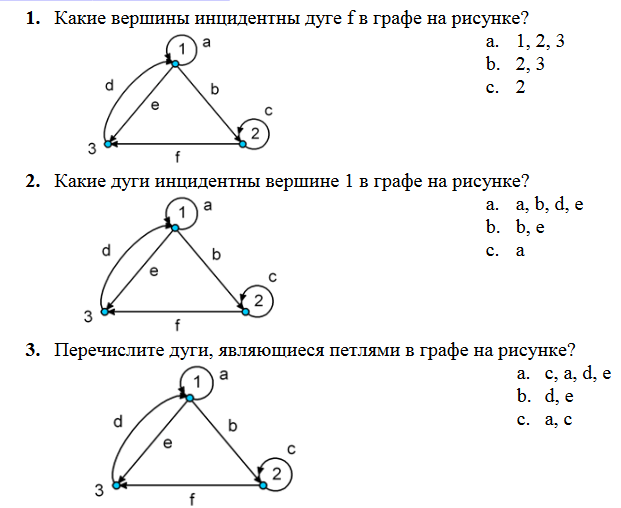
Задание 16. Решить задачи, изобразить получившиеся графы, раскрасить минимальным количеством цветов.

1.На одном изфестивалей встретились 6 делегатов. Оказалось, что из любых троих по меньшей мере двое могут объясниться друг с другом. Докажите, что найдутся три делегата, которые могут объясниться друг с другом.

2. В трехмерном пространстве 9 точек размещены так, что никакие три не лежат на одной прямой. Каждая точка соединена отрезками прямых в точности с четырьмя другими. Докажите, что всегда найдется хотя бы один треугольник с вершинами в этих точках.