Контрольная работа по МАТЕМАТИКЕ за I полугодие

Контрольная работа по МАТЕМАТИКЕ за I полугодие

Вариант 1

Инструкция по выполнению работы

Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.

При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.

Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Справочные материалы

Часть 1

Шоколадка стоит 45 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за три шоколадки, покупатель получает четыре (одну в подарок). Сколько шоколадок можно получить на 350 рублей в воскресенье?

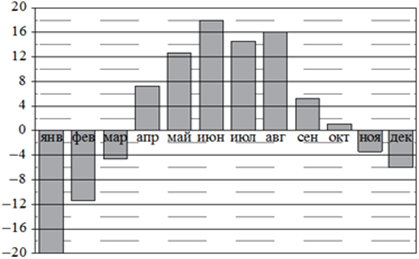
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведённой диаграмме, сколько месяцев среднемесячная температура не превышала 6 градусов Цельсия.

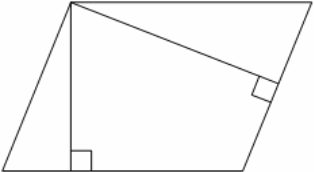
Стороны параллелограмма равны 5 и 10. Высота, опущенная на меньшую из этих сторон, равна 3. Найдите высоту, опущенную на большую сторону параллелограмма.

Биатлонист стреляет два раза по мишени. Вероятность попадания в мишень равна 0,8. Найдите вероятность того, что биатлонист первый раз попадет, а второй раз промахнется.

Решите уравнение  . Если уравнение имеет более одного корня, в ответе укажите сумму корней уравнения.

В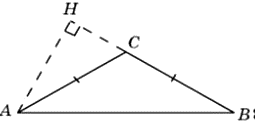  тупоугольном треугольнике ABC стороны AC и BC равны 8, высота AH равна 4. Найдите sin ACB.

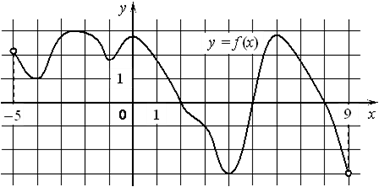
На рисунке изображён график функции   определённой на интервале (− 5; 9). Найдите количество точек, в которых производная функции  равна 0.

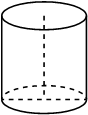
Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра

Часть 2

Найдите значение выражения 

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением   км/ч2. Скорость   (в км/ч) автомобиля вычисляется по формуле  , где   — пройденный автомобилем путь (в км). Найдите, сколько метров проедет автомобиль к моменту, когда он разгонится до скорости 84 км/ч.

От пристани A к пристани B, расстояние между которыми 150 км, отправился с постоянной скоростью первый теплоход, а через 2 ч 30 мин после этого вслед за ним со скоростью, на 10 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт B он прибыл одновременно с первым. Ответ дайте в км/ч.

Найдите наименьшее значение функции   на отрезке 

а) Решите уравнение 

б) Найдите все корни этого уравнения, принадлежащие промежутку

В основании пирамиды   лежит прямоугольник   со сторонами   и  . Известны длины боковых ребер пирамиды: 

а) Докажите, что   высота пирамиды.

б) Найдите угол между плоскостью   и прямой   где   точка пересечения диагоналей прямоугольника 

Решите неравенство