Свойства параллельных прямых
Теоретический материал для самостоятельного изучения.
Ранее мы узнали и научились применять признаки параллельности прямых.
Рассмотрим утверждения, обратные к теоремам, выражающим признаки параллельности двух прямых.
В любой теореме есть две части: условие (это то, что дано)и заключение (это то, что требуется доказать).
Утверждением, обратным данному, называется утверждение, в котором условием является заключение, а заключением – условие.
Итак, вспомним один из признаков параллельности прямых. Если при пересечении двух прямых секущей накрест лежащие углы, образованные этими прямыми и секущей, равны (это условие), то прямые параллельны (заключение).
Сформулируем и докажем обратное утверждение.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы,образованные этими прямыми и секущей,равны.
Дано:
MNՈa =М
MNՈb = N
a║b
∠1 и ∠2 – накрест лежащие.
Доказать: ∠1=∠2.
Доказательство:( метод от противного):
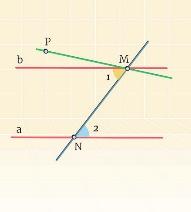
Пусть ∠1≠∠2.
Отложим ∠PMN =∠2 (накрест лежащие) → МР║b→ через точку М проходит 2 параллельные прямые прямой b (МР║b– доказательство;a║b– условие).→∠1=∠2.
Это противоречит теореме о единственности прямой параллельной данной и проходящей через точку.
Теорема доказана.
Рассмотрим следствие.
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
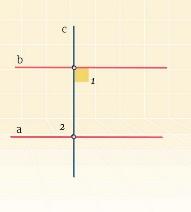
Дано:
a║b
с┴ а
∠1=90°
Доказать: с┴ b.
Доказательство:
С пересекает а, значит, и пересекает параллельную ей прямую b(по следствию из аксиомы параллельных прямых).→ с – секущая к прямым а и b→∠1 = ∠2 = 90° (по только что доказанному свойству параллельных прямых).→ с ┴ b.
Что и требовалось доказать.
Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей соответственные углы равны(это условие), то прямые параллельны(заключение).

Сформулируем и докажем обратное утверждение
Если две параллельные прямые пересечены секущей, то соответственные углы, образованные этими прямыми и секущей, равны.

Дано:
a║b;
с – секущая.
Доказать:
∠1 = ∠2.
Доказательство:
По условию a║b→∠1 = ∠3 (накрест лежащие углы). → ∠2 = ∠3 (вертикальные углы).
Значит, ∠1 = ∠2, что и требовалось доказать.
Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей сумма односторонних углов, образованных этими прямыми и секущей, равна 180° (условие), то прямые параллельны (заключение).

Сформулируем и докажем обратное утверждение.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов, образованных этими прямыми и секущей, равна 180°.

Дано:a║b,
с – секущая.
Доказать:
∠1+∠4= 180°.
Доказательство:
По условию a║b→∠1=∠2 ‑соответственные углы, (в силу предыдущей теоремы).
∠2+∠4=180° (по свойству смежных углов).
→ ∠1+∠4= 180°,что и требовалось доказать.
Материал для углубленного изучения темы.
Задача на доказательство.
Прямая m пересекает параллельные прямые а и b в точках А и В. Прямая р, проходящая через середину отрезка АВ, точку О, пересекает прямые а и b в точках С и D.
Докажем, что ОС=ОD.
По условию дано: а ║b, рՈа= А, рՈb = В, mՈа = D, mՈb = C.
Доказать: ОС = ОD.
Доказательство: рассмотрим, образовавшиеся при построении, треугольники AOD и BOC. Они равны по 2 признаку равенства треугольников, т.к. АО=ВО (О– середина отрезка АВ по условию); ∠1=∠2(накрест лежащие углы); ∠3=∠4 (вертикальные углы). →Все элементы равных треугольников соответственно равны → ОС=ОD. Что и требовалось доказать.

Разбор заданий тренировочного модуля.
1. Три прямых а,р,с пересечены прямой k, при этом образуются соответственные углы: ∠1= 30°,∠2 = 40°,∠3= 30°,как показано на рисунке. Какие из прямых параллельны?

Решение:
На рисунке изображены прямые а, р, с, которые пересечены секущей k. При этом углы 1,2,3 соответственные. По условию: ∠3= ∠1= 30°,∠2 ≠ ∠1,∠2 ≠ ∠3.
Следовательно, прямые а и р параллельные, прямые а и с, р и с не параллельные(по свойствам параллельных прямых).
Ответ: а║р.
2. На рисунке прямые а║b, при этомMO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ, если сумма углов в треугольнике равна 180°?

Решение:
По условию а║b→∠М+∠Е=180° (по теореме о параллельных прямых об односторонних углах). Т.к. MO и ЕО – биссектрисы углов М и Е →∠М = 2∠ОМЕ,
∠Е= 2∠МЕО →
∠М+∠Е =2∠ОМЕ +2∠МЕО =180°.
2(∠ОМЕ +∠МЕО) =180°
∠ОМЕ +∠МЕО =180°:2
∠ОМЕ +∠МЕО =90°.
По условию сумма углов в треугольнике равна 180° → в ∆МОЕ.
∠ОМЕ + ∠МЕО + ∠МОЕ = 180°
90° + ∠МОЕ = 180°
∠МОЕ = 180° – 90° = 90°
Ответ: 90°.
Домашнее задание: 330, 341 решить.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по теме: "Свойства параллельных прямых" (134.37 KB)
Конспект урока по теме: "Свойства параллельных прямых" (134.37 KB)
 0
0 249
249 19
19 Нравится
0
Нравится
0


