КОНСПЕКТ УРОКА
Учитель: Дмитриева Анастасия Михайловна
Предмет: математика Класс: 6
Тема урока: Обыкновенные дроби
Тип урока: Урок обобщения и систематизации знаний.
Цели урока:
систематизировать знания и умения учащихся, связанные с умножением и делением обыкновенных дробей. Упрочить знания слабоуспевающих учеников, упрочить и расширить знания среднеуспевающих школьников, расширить и углубить знания хорошо и отлично успевающих учащихся.
Формы работы на уроке: фронтальная, парная, индивидуальная.
Планируемые результаты:
Предметные: научиться применять приобретенные знания, умения и навыки для решения практических задач.
Метапредметные УУД:
Коммуникативные: учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его.
Регулятивные: оценивать весомость приводимых доказательств и рассуждений.
Познавательные: уметь выделять существенную информацию из текстов разных видов.
Личностные УУД: Формирование навыков анализа, индивидуального и коллективного проектирования
Используемые педагогические технологии: обучение с помощью ИКТ, элементы технологии проблемного обучения, элементы технологий развивающего обучения.
Базовый учебник: Математика: учебник для 6 класса общеобразовательных учреждений Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.- издание.- М.: Мнемозина, 2009
Оборудование: компьютер, мультимедийный проектор, экран, магнитная доска.
Ход урока:
1. Мотивирование к учебной деятельности. Актуализация знаний.
- Здравствуйте, ребята! Прежде чем начать наш с вами урок, попробуйте отгадать следующую загадку: Она бывает барабанная или пальцами, а еще охотничья…. (дробь)
Правильно, дробь!
Обобщим наши знания о дробях, и вспомним правила.
Вопросы
- Сформулируйте правило деления дробей.
- Расскажите, как умножить дробь на натуральное число?
- Расскажите, как выполнить умножение двух дробей.
- Расскажите, как выполнить умножение смешанных чисел.
- Сформулируйте правило нахождения дроби от числа.
- Расскажите, как можно умножить смешанное число на натуральное.
- Как выполняется деление смешанных чисел?
Ответы: - Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю
- Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения.
- Чтобы умножить дробь на дробь: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем, а второе – знаменателем.
- Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильной дроби, а затем воспользоваться правилом умножения дробей.
- Чтобы найти дробь от числа, нужно умножить число на эту дробь.
- Чтобы умножить смешанное число на натуральное число, можно: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на это натуральное число; 3) сложить полученные результаты.
- При делении смешанных чисел: 1) представить смешанные числа в виде неправильных дробей; 2) применить правило деление дробей
2. Сообщение темы урока
Как вы думаете какие действия с дробями мы будем сегодня применять на уроке?
(умножение и деление дробей)
3. Проверка домашнего задания.
Один ученик работает у доски.
4. Письменная работа у доски (эстафета).
Цель: отгадать закодированные числами слова.
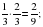 (А)
(А)  (М)
(М)
 (К)
(К)  (А)
(А)
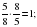 (У)
(У)  (Т)
(Т)
 (З)
(З) 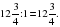 (Е)
(Е)
 (М)
(М)  (М)
(М)
 (А)
(А)  (А)
(А)
Ответ: Акузма, матема
Историческая справка (дает учитель).
Акузма – священное изречение.
Матема – учение, знания, полученные через размышления.
V век. Древняя Греция.
Древние греки знали 4 матема:
учение о числах (арифметика);
теория музыки (гармония);
учение о фигурах и измерениях (геометрия);
астрономия и астрология.
В это время было 2 направления в науке. Первое возглавлял Пифагор, второе – Гиппас Метапонтский.
Пифагор считал, что знания – это священное писание, а наука – дело тайное, только для посвященных. Никто не имеет права делиться своими открытиями с посторонними. Пифагор и его ученики назывались акузматиками.
Гиппас Метапонтский считал, что матема доступна всем, кто способен к продуктивным размышлениям, и называл себя и своих учеников математиками.
Победило второе направление.
Так в V веке возникло слово «математика».
5. Решение задач
Хотя умножение в старину и считалось нелёгким делом, но деление в старину было ещё сложнее, и сохранилась поговорка «Трудное дело деление». Первые методы деления придумал монах из Рима. Не только в Древнем Риме, но и в Древней Греции решали задачи с дробными числами. Решим задачу о знаменитом древнегреческом ученом Пифагоре.
Однажды у Пифагора спросили, сколько у того учеников.
«Охотно скажу, – отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы.
Седьмая часть молча упражняет силу духа, храня в сердце учение.
Добавь ещё к ним трёх юношей.
Столько учеников веду я к рождению вечной истины!»
Сколько учеников было у Пифагора?
(обсуждение решения задачи происходит на интерактивной доске)
После обсуждения один учащийся вызывается к доске и доводит решение до конца.
Пусть у Пифагора было х учеников.
Тогда 1/2x учеников изучают математику,
А 1/4x исследует тайны вечной природы,
И 1/7x упражняет силу духа,
Зная, что было еще 3 ученика составим уравнение:
1/2x+1/4x+1/7x+3=x
x-1/2x-1/4x-1/7x=3
(28-14-7-4)/28x=3
3/28x=3
X=3:3/28
X=(3*28)/3
X=28
6. Работа с учебником.
- Молодцы! Справились с задачкой великого математика.
Откройте учебник на странице 115 и найдите задачку № 718.
Поезд, идущий со скоростью 68 км/ч, проходит расстояние между городами за 6ч. Какое время потребуется велосипедисту, чтобы проехать этого расстояния со скоростью 17 км/ч?
Обсуждение решения этой задачи, один ученик выходит к доске и решает её.
Решение:
Решение:
68 *6 = 408 (км) расстояние между городами
2) 408 *  = 51 (км) 1/8 часть пути
= 51 (км) 1/8 часть пути
3) 51 : 17 = 3 (ч) потребуется велосипедисту
Ответ : 3 часа
7. Релаксация.
Сейчас мы с вами немного отдохнем и расслабимся под спокойную мелодию.
Работа с учебником.
Вот мы с вами отдохнули, и с новыми силами можем приступать к работе .
Откройте учебник на странице 114 и найдите задачку № 715.
В книге 240 страниц. В субботу мальчик прочитал 7,5 % всей книги, а в воскресенье – на 12 страниц больше. Сколько страниц ему осталось прочитать?
Совместное обсуждение решения задачи. Один ученик решает у доски
Решение:
7,5 % = 0,075
1) 240 * 0,075 = 18 (стр.) прочитал в субботу
2) 18 + 12 = 30 (стр.) прочитал в воскресенье
3) 18 + 30 = 48(стр.) прочитал за выходные
4) 240 – 48 = 192 (стр.) осталось прочитать.
Ответ: 192 страницы

 Решение уравнений.
Решение уравнений.
Два ученика решают у доски самостоятельно.
Самостоятельная работа.
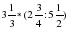 вариант 1.Решите задачу: Поезд прошёл 324 км. Горизонтальный участок пути составляет
вариант 1.Решите задачу: Поезд прошёл 324 км. Горизонтальный участок пути составляет 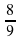 всего пути, подъем -
всего пути, подъем - 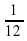 всего пути, а остальная часть пути имеет уклон. Сколько километров прошёл поезд с уклона?
всего пути, а остальная часть пути имеет уклон. Сколько километров прошёл поезд с уклона?
2. Найдите значение выражения:
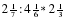 2 вариант : 1.Решите задачу: Три тракториста вспахали 405 га земли. Первый тракторист вспахал
2 вариант : 1.Решите задачу: Три тракториста вспахали 405 га земли. Первый тракторист вспахал  , а второй
, а второй 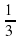 часть от площади вспаханного первым трактористом. Сколько гектаров земли вспахал третий тракторист?
часть от площади вспаханного первым трактористом. Сколько гектаров земли вспахал третий тракторист?
2. Найдите значение выражения:
Взаимопроверка по интерактивной доске.
1 вариант
1. Решение:
1)324 * 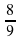 = 288 (км)-горизонтальный участок.
= 288 (км)-горизонтальный участок.
2)324* 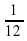 = 27 (км) подъем
= 27 (км) подъем
3) 324-(288+27) = 9(км)- уклон
Ответ: 9 км
2. 
2 вариант
1.Решение:
405 *  = 180 (га) вспахал первый тракторист
= 180 (га) вспахал первый тракторист
2) 180 * 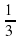 = 60(га) вспахал второй
= 60(га) вспахал второй
3) 405-(180+ 60) = 165(га) вспахал третий.
Ответ: 165 га
2. 
12. Итог урока
И в конце урока, позвольте процитировать замечательные слова Льва Николаевича Толстого: «Человек есть дробь. Числитель – это сравнительно с другими – достоинство человека; знаменатель – оценка человеком самого себя. Увеличить своего числителя – свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя – свое мнение о самом себе».
13.Рефлексия
14. Домашнее задние
п. 13-17, № 642. Найти интересные задачи на арифметические действия с дробями .
6


 Получите свидетельство
Получите свидетельство Вход
Вход



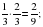 (А)
(А)  (М)
(М) (К)
(К)  (А)
(А)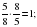 (У)
(У)  (Т)
(Т) (З)
(З) 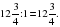 (Е)
(Е)  (М)
(М)  (М)
(М) (А)
(А)  (А)
(А) = 51 (км) 1/8 часть пути
= 51 (км) 1/8 часть пути
 Решение уравнений.
Решение уравнений.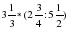 вариант 1.Решите задачу: Поезд прошёл 324 км. Горизонтальный участок пути составляет
вариант 1.Решите задачу: Поезд прошёл 324 км. Горизонтальный участок пути составляет 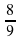 всего пути, подъем -
всего пути, подъем - 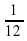 всего пути, а остальная часть пути имеет уклон. Сколько километров прошёл поезд с уклона?
всего пути, а остальная часть пути имеет уклон. Сколько километров прошёл поезд с уклона?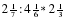 2 вариант : 1.Решите задачу: Три тракториста вспахали 405 га земли. Первый тракторист вспахал
2 вариант : 1.Решите задачу: Три тракториста вспахали 405 га земли. Первый тракторист вспахал  , а второй
, а второй 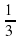 часть от площади вспаханного первым трактористом. Сколько гектаров земли вспахал третий тракторист?
часть от площади вспаханного первым трактористом. Сколько гектаров земли вспахал третий тракторист?








 Конспект урока по математике на тему "Обыкновенные дроби" (57.13 КB)
Конспект урока по математике на тему "Обыкновенные дроби" (57.13 КB)
 0
0 595
595 76
76 Нравится
0
Нравится
0


