Конспект урока по алгебре и начала математического анализа для учащихся 10 класса среднего общеобразовательного учреждения
Тема урока: «Синус и косинус угла»
Цель урока:
Образовательная:
Ввести для учащихся понятия синуса и косинуса угла t; научить их решать простейшие тригонометрические уравнения с использованием данных понятий.
Задачи:
показать важность и необходимость изучения данной темы для учащихся;
дать учащимся определение понятий косинус угла t и синуса угла t;
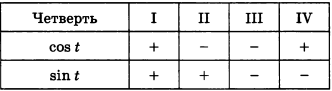
познакомить учащихся с таблицей знаков sin t и cos t по четвертям числовой окружности;
ввести для учащихся основное тригонометрическое тождество;
повторение ранее изученного материала;
ввести таблицу часто встречаемых значений sin t и cos t;
разобрать с учащимися простейшие примеры решения тригонометрических уравнений;
познакомить учащихся со свойствами sin t и cos t.
Развивающая:
Способствовать развитию наблюдательности, логического мышления, памяти, внимания учащихся, их интереса к изучению предмета
Воспитательная:
Воспитать у учащихся дисциплинированности на уроке, аккуратности, трудолюбия, способствовать формированию аргументировано отстаивать свою точку зрения, умение выслушать других
Тип урока: урок усвоения новых знаний
Методы обучения: индуктивно- репродуктивный
Оборудование:
Персональный компьютер, оснащенный ОС Windows 7 Профессиональный; мультимедийный проектор; интерактивная доска; презентация на тему «Синус и косинус угла»
Учебно-методическое обеспечение урока:
Мордкович А.Г. Алгебра и начала математического анализа.10 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А.Г.Мордкович, П.В.Семенов. – 5-е изд., стер.- М.: Мнемозина, 2008. – 424 с.
Мордкович А.Г. Алгебра и начала математического анализа.10 класс. В 2 ч. Ч.2. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В.Семенов. – 5-е изд., стер.- М.: Мнемозина, 2008. – 343 с.
Саранцев Г. И. «Методика обучения математики в средней школе.: учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г.И. Саранцев. – М.: Просвещение, 2002. – 223 с.
Всем кто учится.[Электронный ресурс] /А.Васильев, Санкт-Петербург, 2006г./ Режим доступа: www.aleng.ru
План урока
1. Организационный момент (2 минута)
2. Актуализация знаний (3 минут)
3. Изучение нового материала (12 минут)
4. Закрепление изученного материала (25 минут)
5. Подведение итогов (2 минуты)
6. Домашнее задание (1 минута)
Ход урока
1. Организационный момент включает в себя:
Приветствие учителем учащихся, проверка отсутствующих, готовности помещения к уроку.
2. Актуализация знаний.
Учитель: Ранее нами была изучена тема «Числовая окружность на координатной плоскости». Давайте вспомним основные вопросы из предыдущей темы. Для этого ответьте на следующие вопросы:
чему равно число π в градусной мере?
Ученик: Градусная мера числа π равна 180 градусам.
Учитель: Чему равны координаты числа π/4?
Ученик: Координаты числа π/4 равны (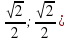
Учитель: Чему равны координаты точки π?
Ученик: Координаты числа π равны (-1;0)
Учитель: Чему равны координаты числа 7π/6?
Ученик: Координаты числа 7π/6 равны (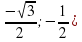
Учитель: Чему равны координаты числа 5π/3?
Ученик: Координаты числа 5π/3 равны (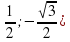
3. Изучение нового материала.
Учитель: Тема нашего сегодняшнего урока «Синус и косинус угла». На этом уроке мы с вами дадим определение косинуса и синуса угла t, научимся решать простейшие тригонометрические уравнения,. которые могут вам пригодиться в дальнейшем при изучении тригонометрических функции, решение сложных тригонометрических уравнений, при решении задач в ЕГЭ, а так же это пригодится тем кто пойдет в ВУЗ на экономическую, педагогическую, строительную специальности.
А теперь откроем тетради, запишем число, классная работа, и тему нашего сегодняшнего урока «Синус и косинус».
Запись на доске и в тетрадях:
25.11.2014
Классная работа.
Синус и косинус угла.
Учитель:
В курсе геометрии были введены понятия синуса и косинуса угла, выраженного в градусах. Этот угол рассматривался в промежутке от 0° до 180°.
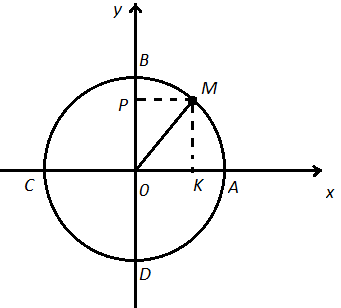
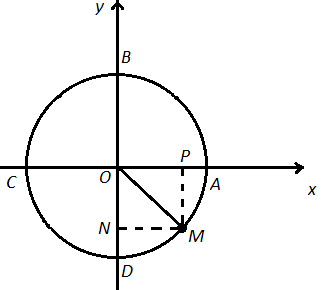
Рассмотрим единичную окружность на координатной плоскости. Выберем на ней произвольный угол t, которому будет соответствовать единственная точка на числовой окружности М с координатами (х; у). Координату х назовем косинусом угла t, а координату y назовем синусом угла t.
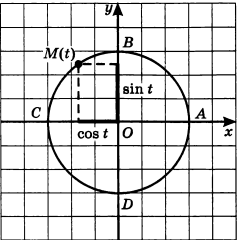
Учитель: Тогда синус и косинус произвольного угла определяется следующим образом:
Если точка М числовой окружности соответствует углу t, то абсциссу точки М называют косинусом угла t и обозначают cos t, а ординату точки М называют синусом угла t и обозначают sin t.
Кстати что такое координатная плоскость?
Ученик: Это плоскость, на которой выбрана система координат.
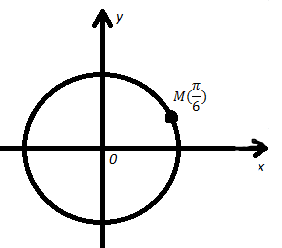
Учитель: Рассмотрим конкретный пример. Давайте найдем координаты точки М если она будет равна 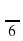 . По только что данному определению мы теперь знаем, что косинус угла это абсцисса этой точки, а синус угла это ордината точки.
. По только что данному определению мы теперь знаем, что косинус угла это абсцисса этой точки, а синус угла это ордината точки.
Какие координаты будут у этой точки?
Ученик: Координаты этой точки будут равны (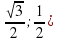
Учитель: Тогда чему будет равен косинус этого угла? Не забываем что косинус угла t это абсцисса точки.
Ученик: Если косинус угла t это абсцисса, то тогда он будет равен 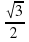
Учитель: А чему будет равен синус угла?
Ученик: Если синус угла t это ордината, то тогда он будет равен 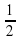
Учитель: На предыдущем уроке мы так же отметили что для любой точки M(x;y) числовой окружности выполняются неравенства 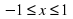 ;
;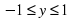 . Отсюда мы получаем, что
. Отсюда мы получаем, что
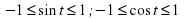
Что бы знать знаки синуса угла t и косинуса угла t, которые нам понадобятся в дальнейшем при решении задач, давайте составим следующую таблицу.
Если точка лежит в первой четверти, то по рисунку мы видим что координаты 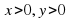 , а мы теперь знаем, что x это COS t,а y это SIN t, тогда значит, что
, а мы теперь знаем, что x это COS t,а y это SIN t, тогда значит, что 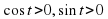 .
. 
Учитель: Если точка лежит во второй четверти, то по рисунку видим что 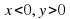 , тогда
, тогда 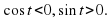
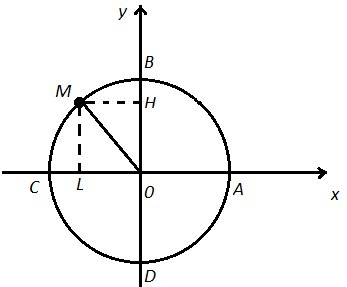
Учитель: Если точка лежит в третьей четверти, то по рисунку видно, что 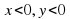 , значит
, значит 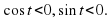
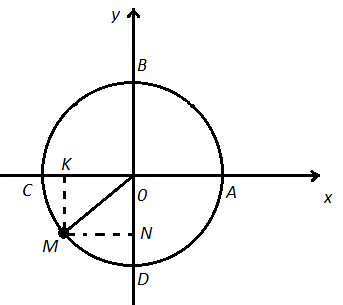
Учитель: И в четвертой четверти 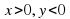 мы получаем, что
мы получаем, что 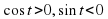 .
.
Учитель: Как выглядит уравнение числовой окружности?
Ученик: Уравнение числовой окружности имеет вид 
Учитель: А так же мы знаем, что x=cos t;y=sin t значит  это основное тригонометрическое тождество.
это основное тригонометрическое тождество.
На предыдущем уроке мы заостряли внимание на том, как важно научиться отыскивать координаты некоторых точек числовой окружности. А так как мы теперь знаем что x это cos t, а y это sin t, то мы можем составить таблицу часто встречаемых значений sin t и cos t.
(На слайде выводится таблица, которую предстоит заполнить)
Запись в тетрадях:
Учитель: Мы теперь с вами знаем, что косинус угла это абсцисса, а синус угла это ордината, тогда чему будут равны синус 0° и косинус 0°?
Ученик: Синус 0° будет равен 0, а косинус 0° будет равен 1.
(Далее таблица заполняется аналогично)
Запись в тетради:
Учитель: Теперь давайте рассмотрим свойства синуса и косинуса угла:
Свойство 1: Для любого угла t справедливы равенства:
Построим точку М которая будет соответствовать углу t на числовой окружности, и точку Р которой будет соответствовать угол (-t) на числовой окружности, точка Р симметрична точке М относительно оси абсцисс. У этих точек одна абсцисса, а это значит что .И у таких точек равные по модулю, но противоположные по знаку ординаты, что говорит о том что
Запись в тетради:
Учитель: Давайте рассмотрим пример, надо вычислить 
По только что изученному нам свойству, знак минус у аргумента синуса мы можем вынести вперед, и получаем что 
 ,а мы знаем, что
,а мы знаем, что  равен ½, а так как еще перед функцией стоит знак минус, то мы получаем, что
равен ½, а так как еще перед функцией стоит знак минус, то мы получаем, что 
Запись на доске в тетради:
Учитель: Свойство 2: Для любого угла t справедливы равенства:
Это очевидно, поскольку числам t и t+2πk соответствует одна и та же точка числовой окружности.
Запись в тетради:
Свойство 2: Для любого угла t справедливы равенства:
Учитель: Свойство 3: Для любого угла t справедливы равенства:
Учитель: Если числу t соответствует точка М числовой окружности, то числу t+π соответствует точка Р, симметричная точке М относительно центра окружности – начала координат. У таких точек абсциссы равны по модулю, но противоположны по знаку, и ординаты равны по модулю, но противоположны по знаку. А это значит, что
Запись в тетради:
Свойство 3: Для любого числа t справедливы равенства:
Учитель: Давайте рассмотрим пример:
Вычислить 
 мы можем расписать как
мы можем расписать как  , а по только что пройденному нами свойству мы можем отбросить π и поставить знак минус перед
, а по только что пройденному нами свойству мы можем отбросить π и поставить знак минус перед  , а
, а  это табличное значение и он равен
это табличное значение и он равен  , а так как у нас стоит еще и минус то
, а так как у нас стоит еще и минус то 
Запись на доске в тетради:
4. Закрепление первичного материала
Учитель: А теперь давайте вычислим cos t;sin t если: ( №13.3 а,б)
Ученик:
 мы можем записать как
мы можем записать как  , а 2π, а по только что изученным нам свойствам мы может отбросить, тогда мы получаем
, а 2π, а по только что изученным нам свойствам мы может отбросить, тогда мы получаем  , а это уже табличное значение которое равно
, а это уже табличное значение которое равно 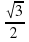
Аналогично с синусом угла, мы можем отбросить 2π и получаем, что  , а
, а  это табличное значение которое равно ½
это табличное значение которое равно ½
Запись на доске и в тетради:
=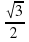
 =
=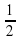
(Следующий пример решается аналогично.)
Запись на доске и в тетради:
 =
=
=
Учитель: решить уравнение  =
=
Используем числовую окружность. Где наш синус угла принимает значение 0?
Ученик: Синус угла принимает значение 0 в углах 0° и π.
Учитель: А как мы можем записать их в виде формул?
Ученик: Для первого угла формула будет выглядеть следующим образом t1=0 + 2πk и для второго угла такая t2=π+2πk.
Учитель: А мы можем объединить эти решения?
Ученик: Да можем
Учитель: Тогда что мы получим?
Ученик:
 k
k  Z
Z
Запись на доске и в тетради:
 =
=
t1=0 + 2πk ; t2=π+2πk.

 k
k  Z
Z
Учитель: решить уравнения  =
=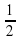
Запись на доске в тетради:
 =
=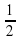

 , k
, k  Z
Z
Учитель: Следующий номер 13.4.(а,б). Для решения этого номера нам понадобятся свойства синуса и косинуса, которые мы с вами изучили.
Ученик: Так как мы теперь знаем свойство, что знак у аргумента синуса выносится вперед, то мы можем записать, что .  так и остается. А у косинуса только что по изученному свойству минус можно убрать, тогда . Тогда мы получаем следующее выражение +
так и остается. А у косинуса только что по изученному свойству минус можно убрать, тогда . Тогда мы получаем следующее выражение + , а мы знаем что ,
, а мы знаем что ,  , а , таким образом мы получаем
, а , таким образом мы получаем
Запись на доске и в тетради:

+ =
=
б)
5. Подведение итогов
Учитель: Что нового вы сегодня узнали?
Ученик: Сегодня мы узнали, как можно определить косинус и синус с помощью числовой окружности. Так же мы узнали как решать простейшие тригонометрические уравнения.
6.Домашнее задание
Учитель: Теперь запишите домашнее задание. П. 13 – выучить знаки и значения синуса и косинуса угла, и номера 13.1.,13.4.(в, г),13.5.(а) Спасибо, можете быть свободны.


 Получите свидетельство
Получите свидетельство Вход
Вход


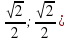
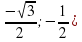
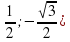

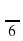 . По только что данному определению мы теперь знаем, что косинус угла это абсцисса этой точки, а синус угла это ордината точки.
. По только что данному определению мы теперь знаем, что косинус угла это абсцисса этой точки, а синус угла это ордината точки.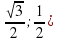
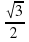
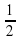

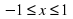 ;
;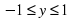 . Отсюда мы получаем, что
. Отсюда мы получаем, что 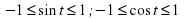
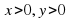 , а мы теперь знаем, что x это COS t,а y это SIN t, тогда значит, что
, а мы теперь знаем, что x это COS t,а y это SIN t, тогда значит, что 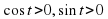 .
. 
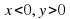 , тогда
, тогда 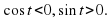

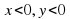 , значит
, значит 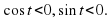

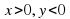 мы получаем, что
мы получаем, что 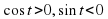 .
. 










 Конспект урока по алгебре "Синус и косинус угла" (0.32 MB)
Конспект урока по алгебре "Синус и косинус угла" (0.32 MB)
 0
0 4411
4411 1152
1152 Нравится
0
Нравится
0