
O’zbekiston Respublikasi Xalq
Ta’limi Vazirligi
Namangan viloyati xalq ta’limi boshqarmasi
Namangan tumani XTB ga qarashli 11-sonli umumiy o’rta ta’lim maktabi
MATEMATIKA FANI O’QITUVCHISI EGAMBERDIYEVA NARGIZANING
9-sinf ALGEBRA fanidan
“KELTIRISH FORMULALARI ” MAVZUSIDA
Yozgan bir soatlik

Namangan tuman
DARSNING TEXNOLIGIK XARITASI
| Mavzu: Tayanch so’zlar: | Keltirish formulalari davriy funksiyalar eng kichik musbat davr kosinus uchun keltirish formulasi sinus uchun keltirish formulasi tangens uchun keltirish formulasi
|
| Mavzuning qisqacha ta’rifi: | Ushbu mavzu orqali o’quvchilarni darslik va dasturlar hamda undan tashqari adabiyotlar, internet ma’lumotlari asosida keltirish formulalari haqida bilim, ko’nikma va malakalar hosil qilish. |
| O’quv jarayonini amalga oshirish texnologiyasi: Shakl: Uslub: Vositalar: |
amaliy bajarish guruhlarda ishlash Darslik, ko’rgazmali qurollar, proyektor |
| Dars (amaliyot)ining maqsad va vazifalari | |
| Maqsadlar: Ta’limiy: Tarbiyaviy:
Rivojlantiruvchi: |
O’quvchilarga keltirish formulalari haqidagi bilimlar berish. O’quvchilarga keltirish formulalariga oid tushunchalar orqali estetik tarbiya berish o’quvchilarni ziyraklik, topqirlik va zukkolikka o’rgatish. O’quvchilarni fanga bo’lgan qiziqishlarini orttirish,mustaqil fikrlash qobiliyatini rivojlantirish |
| Kutilayotgan natijalar | |
| Dars(amaliyot)yakunida o’quvchi biladi(bilim): | keltirish formulalarini qo’llagan holda masalalar yecha oladi.
|
| Dars (amaliyot) yakunida o’quvchi tushunadi (ko’nikma): | O’quvchilarga keltirish formulalari mohiyatini o’rgatish. |
| Dars (Amaliyot)yakunida o’quvchi bajara oladi (malaka) | Har hil misol va masalalar yechishda keltirish formulalarini qo’llay olish. |
Darsning bajarilish bosqichlari
| Bosqichlar | Bajariladigan ish mazmuni | Uslub | Vaqt (min) |
| 1- bosqich: Tashkiliy qism | Psixologik muhit yaratish. O’quvchilarni darsga tayyorlash | Savol -javob muloqot |
2 |
| 2-bosqich: (Reflektsiya) Ehtiyojlarni aniqlash | O’tgan mavzu yuzasidan savol javob o’tkazish orqali tushuncha bilim, ko’nikma, malakalarni mustahkamlash | Aqliy hujum Tezkor savol-javob Krossvord Zanjir Do’stingni top |
10 |
| 3-bosqich: Yangi mavzu bayoni | Reja davriy funksiyalar eng kichik musbat davr kosinus uchun keltirish formulasi sinus uchun keltirish formulasi tangens uchun keltirish formulasi
Masalalar ishlash | Mavzuni o’quvchilar daftariga qayd ettirib borish | 15
|
| 4-bosqich: Mustahkamlash: | Keltirish formulalarini misollar yechish jarayonida qo’llay olish | Guruhlarga bo’lib ishlash | 13 |
| 5-bosqich: baholash
| Darsda faol ishtirok etgan o’quvchilarni rag’batlantirish. O’quvchilarga tushunmaganlarini tushuntirish | Savol javob tushuntirish ishlari | 3 |
| 6-bosqich: Uyga vazifa
| Masala | Tushunitirsh ishlari | 2 |
Shakllantiriladigan kompetensiyalar:
1.Kommunikativ kompetensiya:
Mavzuga oid tushunchalar davriy funksiyalar eng kichik musbat davr,kosinus uchun keltirish formulasi,sinus uchun keltirish formulasi,tangens uchun keltirish formulasi ) ma’nosini tushunadi va to’g’ri ifodalay oladi.
2.Axborotlar bilan ishlash kompetensiyasi:Tavsiya etilgan manbalar(internet,elektron darsliklar,adabiyotlar) dan axborotni izlab topa oladi.
Darsning borishi
I.Tashkiliy qism: Salomlashish,yo’qlama olish
O’quvchilar- Assalomu alaykum,aziz ustoz muallim,
Bizlar shaymiz saboqqa, siz bizga bering ta’lim.
O’qituvchi- Va alaykum assalom aziz o’quvchilarim,
Kuch bo’lsin sizga hamroh,olingizlar ko’p ilm.
Navbatchi shaymi,ma’lumot bersin endi
Navbatchi bugungi kun,yo’qlama ma’lumotini beradi.o’quvchilarga teskari holda qo’yilgan tarqatma materiallarni bittadan olishlari kerakligini o’qituvchi ta’kidlaydi. Tarqatmalar uch xil rangga bo’yalgan bo’ladi. Bir xil rangni tortganlar bir jamoa bo’lishadi. Shu usul orqali sinf uch guruhga ajratiladi. Guruhlar o’zlariga nom beradilar.Misol uchun 1-guruh “Topqirlar”, 2-guruh “Epchillar”, 3-guruh “Bilimdonlar”.
O’qituvchi: Hurmatli o’quvchilar. Bugungi darsimizni “Omad shou” tarzida tashkil etamiz. Bu o’yin tarzida bo’lib uch guruh baxs yuritadi. Men uch guruhdan bir nafardan istirokchini taklif qilaman. Ular barabanni aylantirgan holda bir-birlariga shart tanlab beradilar. 1-guruh o’quvchisi 2- guruh o’quvchisiga, 2-guruh o’quvchisi 3-guruh o’quvchisiga, 3-guruh o’quvchisi esa 1-guruh o’quvchisiga shat tanlab beradilar. (Xattaxtaga o’yin uchun 12 bo’lak bilan ajratilgan va nomerlangan baraban va 12 ta shart yozilgan ko’rgazmalar ilingan bo’ladi). 
Barabanni 1-guruh o’quvchisi aylantirdi va 5 raqami tushdi . yonidagi ko’rgazmadan 5-raqamdagi shart tortiladi. Misol uchun “Tezkor savol javob ” sharti tusdi deylik. Bu shartni 2-guruh o’quvchilari bajaradilar. 2-guruhdagi har bir o’quvchi uchun birin ketin savollar beriladi va ular tezlik bilan javob berishlari kerak bo’ladi.
“Tezkor savol-javob”
Asosiy trigonometrik ayniyat ? (sin2 α+cos2 α)
Sinusning 3-chorakdagi ishorasi ? (minus)
Tangens nimaga teng? (sin α /cos α)
Ikkilangan burchak sinusi nimaga teng? (2sin α cos α)
Kotangensning 4-chorakdagi ishorasi ? (minus)
Ikkilangan burchak kosinusi nimaga teng? (cos2 α -sin2 α)
Cos600 dagi qiymat? (1/2)
Tg 450 da nechga teng? (1)
Shu tarzda 2-guruh 3-guruhga shart tanlaydi. “Zanjir” o’yini tushdi deylik. 3-guruh trigonometrik formulalardan aytgan holda bir- birlarini ushlab “Zanjir” hosil qiladilar. Agar barcha o’quvchi formula ayta olsa “Zanjir” mustahkkam, agar kimdir ayta olmasa o’sha o’quvchi zanjirni uzgan bo’ladi. “Zanjir” to’liq hosil qilinsa barcha o’quvchilar baravar- Zanjirimiz uzilmasin
Do’tligimiz buzilmasin deydilar.
Keyingi shart “Do’stingni top” o’yini . Bu o’yinda o’quvchilar qo’llariga formulalarning o’ng va chap qismlari alohida yozilgan holda tarqatiladi. Har bir o’quvchi o’z qo’lidagi formulani davomi kimda ekanligini ya’ni do’stlarini topadilar.
Qolgan shartlarni “Krossvord”, “Geyzer”, “Qaror aytish”, “Maqol aytish”va hokazo tarzida tanlasa bo’ladi.
Har bir shartni bajargan o’quvchi qo’liga rag’bat kartochkasi berib boriladi. Bajara olmagan o’quvchi uchun jarima kartochkasi beriladi.
Yangi mavzu o’qituvchi tomonidan xattaxtaga yoziladi:
Keltirish formulalari
Sinus, kosinus, tangens va kotangens qiymatlarining jadvallari 0° dan 90° gacha (yoki 0 dan ![]() gacha) burchaklar uchun tuziladi. Bu hol ularning boshqa burchaklar uchun qiymatlari o'tkir burchaklar uchun qiymatlariga keltirilishi bilan izohlanadi.
gacha) burchaklar uchun tuziladi. Bu hol ularning boshqa burchaklar uchun qiymatlari o'tkir burchaklar uchun qiymatlariga keltirilishi bilan izohlanadi.
1-masala. sin870° va cos870° ni hisoblang.
D 870° = 2·360° + 150°. Shuning uchun P(1; 0) nuqtani koordinatalar boshi atrofida 870° ga burganda, nuqta ikkita to'la aylanishni bajaradi va yana 150° burchakka buriladi, ya'ni 150° ga burishdagi M nuqtaning xuddi o'zi hosil bo'ladi (1- rasm).
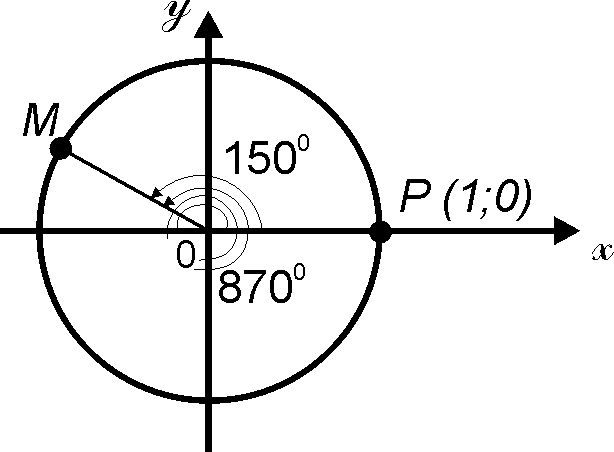
1-rasm.
Shuning uchun sin870° = sin150°, cos870° = cos150°.
M nuqtaga Oy o'qqa nisbatan simmetrik bo'lgan M1 nuqtani yasaymiz (2- rasm).
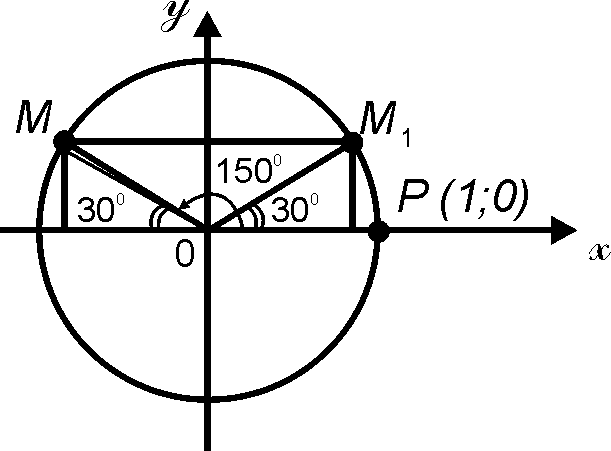
2-rasm.
M va M1 nuqtalarning ordinatalari bir xil, abssissalari esa faqat ishoralari bilan farq qiladi. Shuning uchun sin150° = sin30° = ![]() ; cos150° = -cos30° =
; cos150° = -cos30° = ![]() .
.
Javob: sin870°=![]() , cos870°=
, cos870°=![]() .
. ![]()
1-masalani yechishda
sin(2·360° + 150°) = sin150°, cos(2·360° + 150°) = cos150°, (1)
sin(180°-30°) = sin30°, cos(180°-30°) = -cos30° (2)
tengliklardan foydalanildi.
(1) tenglik to'g'ri tenglik, chunki P(1; 0) nuqtani
![]() burchakka burganda, uni a burchakka burgandagi nuqtaning ayni o'zi hosil bo'ladi.
burchakka burganda, uni a burchakka burgandagi nuqtaning ayni o'zi hosil bo'ladi.
Shuning uchun ushbu formulalar to'g'ri bo'ladi:
sin(a + 2pk) = sina,
cos(a + 2pk) = cosa, ![]()
Xususan, k = 1 bo'lganda:
![]()
tengliklar o'rinlidir.
![]() formulani isbot qilamiz.
formulani isbot qilamiz.
D Sinus uchun qo'shish formulasini qo'llab, hosil qilamiz:
![]() .
. ![]()
(4) formulalarning ikkinchisi ham shunga o'xshash isbot qilinadi. (4) formulalar keltirish formulalari deyiladi. (3) va (4) formulalar yordamida istalgan burchakning sinus va kosinusini hisoblashni ularning o'tkir burchak uchun qiymatlarini hisoblashga keltirish mumkin.
2-masala. sin930° ni hisoblang.
D (3) formuladan foydalanib, hosil qilamiz:
sin930° = sin(3·360° - 150°) = sin(-150°).
![]() formula bo'yicha sin(-150°) = -sin150° ni hosil qilamiz.
formula bo'yicha sin(-150°) = -sin150° ni hosil qilamiz.
(4) formula bo'yicha topamiz:
- sin150° = - sin(180° - 30°) = - sin30° = ![]() .
.
Javob: 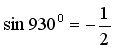 .
. ![]()
3-masala. 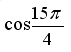 ni hisoblang.
ni hisoblang.
D ![]() .
.![]()
Endi istalgan burchakning tangensini hisoblashni o'tkir burchakning tangensini hisoblashga qanday keltirish mumkinligini ko'rsatamiz.
(3) formuladan va tangensning ta'rifidan
![]() tenglik kelib chiqadi.
tenglik kelib chiqadi.
Bu tenglik va (4) formuladan foydalanib, hosil qilamiz:
.
Shuning uchun ushbu formula o'rinli bo'ladi:
4-masala. Hisoblang: 1) ; 2)
.
D 1) .
2) .
formulalar isbotlangan edi, ular ham keltirish formulalari deb ataladi. Bu formulalardan foydalanib, masalan, ,
ni hosil qilamiz.
x ning istalgan qiymati uchun tengliklar to'g'riligi ma'lum.
Bu tengliklardan ko'rinadiki, argument ga o'zgarganda, sinus va kosinusning qiymatlari davriy takrorlanadi. Bunday funksiyalar davri
bo'lgan davriy funksiyalar deyiladi.
Agar shunday son mavjud bo'lsaki, у= f(x) funksiyaning aniqlanish sohasidagi istalgan x uchun f(x - T) = f(x) = f(x + T) tenglik bajarilsa, f(x) davriy funksiya deb ataladi. T son f(x) funksiyaning davri deyiladi
Bu ta'rifdan ko'rinadiki, agar x son f(x) funksiyaning aniqlanish sohasiga tegishli bo'lsa, u holda x + T, x - T sonlar va, umuman, x + Tn, sonlar ham shu davriy funksiyaning aniqlanish sohasiga tegishli va f(x + Tn) = f(x),
bo'ladi.
soni у =cosx funksiyaning eng kichik musbat davri ekanini ko'rsatamiz.
D T 0 kosinusning davri bo'lsin, ya'ni istalgan x uchun
cos(x + T) = cosx tenglik bajariladi. x = 0 deb, cosT = 1 ni hosil qilamiz. Bundan esa ,
![]() . T 0 bo'lganidan, T quyidagi
. T 0 bo'lganidan, T quyidagi qiymatlarni qabul qila oladi va shuning uchun T ning qiymati
dan kichik bo'lishi mumkin emas.
![]()
у = sinx funksiyaning eng kichik musbat davri ham ga teng ekanini isbotlash mumkin
Mavzuni mustahkamlash
1. Keltirish formulalari deganda, nimani tushunasiz?
2. Keltirish formulalarining mohiyati nimadan iborat?
3. Sinus uchun keltirish formulasini tushuntiring.
4. Kosinus va tangens uchun keltirish formulalarini yozing.
Hisoblang (352-355):
352. 1) ; 2)
; 3)
;
4) ; 5) sin720°; 6) cos540°;
353. 1) cos420°; 2) tg570°; 3) sin3630°;
4) ctg960°; 5) ; 6)
.
354. 1) cos150° 2) sin135° 3) cos120°; 4) sin315°.
355. 1) ; 2)
; 3)
;
4) ; 5)
; 6)
.
356. Ifodaning son qiymatini toping:
1) cos630° - sin1470° - ctg1125°;
2) tg1800° - sin495° + cos945°;
3) ;
4) .
357. Ifodani soddalashtiring:
1) ;
2) .
O’quvchilarga monitor orqali test savollari beriladi.
1-savol
|
| Ushbu |
|
| - |
|
| -2 |
|
| -1 |
|
| 1 |
2-savol
|
|
|
|
|
|
|
| -1 |
|
| - |
|
| 1 |
3-savol
|
| Hisoblang: |
|
|
|
|
|
|
|
|
|
|
|
|
4-savol
|
| Hisoblang: |
|
| 0 |
|
| -1 |
|
| 2 |
|
| 1 |
5-savol
|
| Hisoblang: |
|
| 1 |
|
| -1 |
|
|
|
|
|
|
6-savol
|
| Hisoblang: |
|
| 1,5 |
|
| 1 |
|
| 0,5 |
|
| 0,75 |
7-savol
|
| Keltirilgan sonlardan eng kattasini toping. |
|
| sin1 |
|
| cos1 |
|
| sin4 |
|
|
|
8-savol
|
| Ifodani soddalashtiring: |
|
| 2 |
|
| 1 |
|
| cosx |
|
| sinx |
9-savol
|
| Noto'g'ri tenglikni ko'rsating. |
|
| cos(-x) = -cosx |
|
| cos(p + x) = -cosx |
|
| tg(2p - x) = -tgx |
|
| tg(p + x) = tgx |
10-savol
|
|
|
|
|
|
|
| - |
|
| 1 |
|
| -1 |

 Получите свидетельство
Получите свидетельство Вход
Вход











 Келтириш формулалари (543.43 KB)
Келтириш формулалари (543.43 KB)
 0
0 1776
1776 5
5 Нравится
0
Нравится
0








