Итоговая контрольная работа по математике
за курс 8 класса
подготовила учитель математики
МАОУСОШ№ 8 города Черняховска
Гузикене Наталья Владимировна.
Работа рассчитана на 45 минут.
Состоит из двух частей.
Задания из первой части оцениваются 1 баллом, второй части – задания 1 и 2 – по 2 балла, задания 3 и 4 по 3 балла.
Итого вся работа – 20 баллов.
Оценка за работу выставляется отдельно по геометрии и по алгебре, если предметы изучались раздельно.
Минимальное количество баллов
по алгебре - 5 баллов, по геометрии – 3 балла.
вариант 1 Часть 1
Алгебра
Вычислите: 5∙ 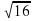 + 8∙
+ 8∙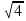
2. Найдите значение выражения 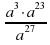 при а = 0,4.
при а = 0,4.
3. Упростите выражение: 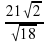 .
.
4. Выполните сложение дробей 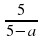 +
+ 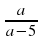 , если а≠ 5.
, если а≠ 5.
5. Решите уравнение и в ответе запишите сумму корней: 5х2 – 8х +3 = 0
6. На каком рисунке изображено множество решений неравенства 4х + 5 ≥ 6х - 2?
1) 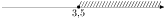
2) 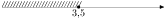
3) 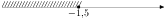
4) 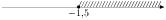
Геометрия
1. Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны.
2) Если расстояние от центра окружности до прямой равно диаметру окружности, то эти прямая и окружность касаются.
3) Если радиус окружности равен 2, а расстояние от центра окружности до прямой равно 3, то эти прямая и окружность не имеют общих точек.
4) Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.
2. В параллелограмме один из углов 40⁰. Найти градусную меру остальных углов параллелограмма.
3. Найдите площадь фигуры.
4. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 20 км/ч и 21 км/ч. Какое расстояние (в километрах) будет между ними через 1 час?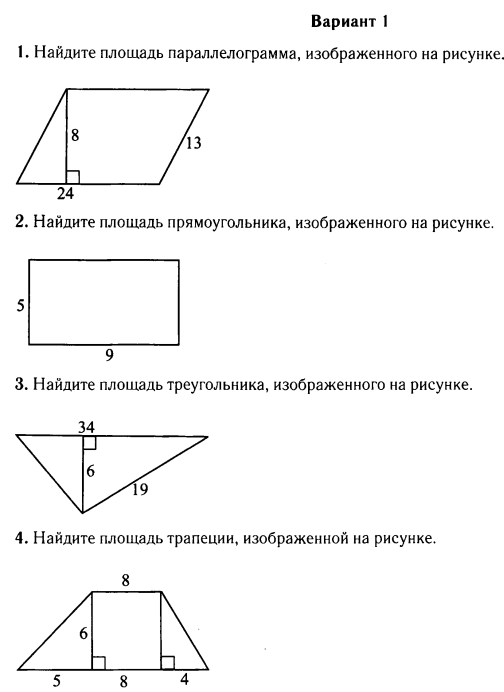
Часть 2.
1. Решите уравнение: 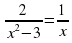 .
.
2. Найдите периметр параллелограмма ABCD, если известно, что биссектриса его острого угла AF делит его большую сторону ВС на отрезки длиной BF = 5см, FC = 2 см.
3.Из пунктов А и В, расстояние между которыми 19 км вышли одновременно навстречу друг другу два туриста и встретились в 9 км от пункта А. Найдите скорость туриста, вышедшего из пункта А, если известно, что он шел со скоростью, на 1км/ч большей, и сделал в пути 30-минутный привал.
4. В прямоугольной трапеции ABCD меньшее основание равно меньшей боковой стороне. Диагональ, проведенная из вершины тупого угла, перпендикулярна большей боковой стороне, равной 8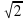 см. Найдите площадь трапеции.
см. Найдите площадь трапеции.
вариант 2
Часть 1
алгебра
1. Вычислите: 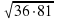
2. Найдите значение выражения 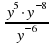 при у = 2.
при у = 2.
3. Расположите в порядке возрастания числа: 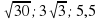 .
.
4. Выполните действие: 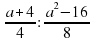 .
.
5. Решите уравнение и в ответе напишите разность корней: 2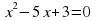
6 . На каком рисунке изображено множество решений неравенства х2 + х – 6 ≥ 0.

Геометрия
1. Какие из следующих утверждений верны?
1) Если вписанный угол равен 30°, то центральный угол, опирающийся на ту же дугу окружности, равен 60°.
2) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 5, то эти прямая и окружность не пересекаются.
3) Если дуга окружности составляет 80°, то центральный угол, опирающийся на эту дугу, равен 40°.
2. В прямоугольной трапеции угол при меньшем основании равен 28 ⁰. Найдите остальные углы трапеции.
3. Два парохода вышли из порта, следуя один на юг, другой на запад. Скорости их равны соответственно 24 км/ч и 10 км/ч. Какое расстояние (в километрах) будет между ними через 1 час?
4. Периметр квадрата 36 см. Чему равна его площадь?
Часть 2.
1. Решите уравнение: 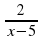 =
= 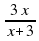 .
.
2. Основания равнобедренной трапеции равны 10 см и 18 см, а боковая сторона равна 5 см. Найдите площадь трапеции.
3. Автобус был задержан с выездом на 9 минут. Чтобы прибыть в пункт назначения вовремя, водитель увеличил намеченную скорость на 10 км/ч. Найдите первоначальную скорость автобуса, если расстояние, которое он проехал, равно 30 км.
4. В равнобедренном треугольнике ABC с основанием AC угол при вершине B равен 120⁰, CD – высота. Найдите длину AD, если высота, проведенная к основанию, равна 10 см.
вариант 3
Часть 1
алгебра
1. Вычислите: 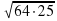

2. Найдите значение выражения 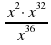 при х = 0,5
при х = 0,5
3. Упростите выражение: 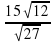 .
.
4. Выполните действие  .
.
5. Решите уравнение и в ответе запишите наименьший корень 2х2 + 9х + 9 = 0.
6. На каком рисунке изображено множество решений неравенства 2х + 1
геометрия
1. Какие из следующих утверждений верны?
1) Если дуга окружности составляет 80°, то центральный угол, опирающийся на эту дугу, равен 40°.
2) Вписанные углы окружности равны.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
2. В равнобедренной трапеции угол при большем основании равен 42 ⁰. Найдите остальные углы трапеции.
3. Найдите площадь фигуры , изображенной на клетчатой бумаге с размером клетки 1см х1 см.
4. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 16 км/ч и 30 км/ч. Какое расстояние (в километрах) будет между ними через 1 час?
Часть 2.
1. Решите уравнение:  =
=  .
.
2. Найдите периметр параллелограмма ABCD, если известно, что биссектриса его острого угла AF делит его большую сторону ВС на отрезки длиной BF= 4см, FC = 2 см.
3.Два велосипедиста одновременно отправились в 108-километровый пробег. Первый ехал со скоростью на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час 48 минут раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.
4. В прямоугольной трапеции меньшее основание равно 6 см, а меньшая боковая сторона равна 2 см. Найдите площадь трапеции, если один из ее углов равен 120⁰.
см. Найдите площадь трапеции, если один из ее углов равен 120⁰.
вариант 4
Часть 1
алгебра
1. Вычислите: 
2. Найдите значение выражения  при с = 5.
при с = 5.
3. Расположите в порядке убывания числа:  .
.
4. Выполните действие:  ·
· 
5. Решите уравнение и в ответе напишите больший корень: 
6. На каком рисунке изображено множество решений неравенства х2 - 4х + 3 ≥ 0
Геометрия
1. Какие из следующих утверждений верны?
1) Если радиус окружности равен 5, а расстояние от центра окружности до прямой равно 3, то эта прямая – касательная к окружности.
2) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
3) Касательная к окружности перпендикулярна радиусам данной окружности.
2. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
3. Найдите площадь трапеции, изображённой на рисунке.
4. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
Часть 2.
1. Решите уравнение:  .
.
2. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
3. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
4. В равнобедренном треугольнике ABC АВ = АС = 40 см, угол при вершине B равен 120⁰, CD – высота. Найдите длину AD.


 Получите свидетельство
Получите свидетельство Вход
Вход



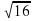 + 8∙
+ 8∙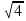
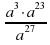 при а = 0,4.
при а = 0,4. 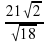 .
.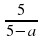 +
+ 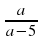 , если а≠ 5.
, если а≠ 5.
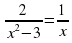 .
.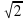 см. Найдите площадь трапеции.
см. Найдите площадь трапеции.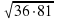
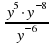 при у = 2.
при у = 2.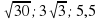 .
. 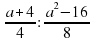 .
.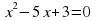

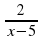 =
= 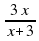 .
.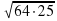

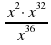 при х = 0,5
при х = 0,5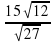 .
.








 Итоговая контрольная работа по алгебре и геометрии (0.37 MB)
Итоговая контрольная работа по алгебре и геометрии (0.37 MB)
 0
0 3813
3813 282
282 Нравится
0
Нравится
0


