Итоговый тест по теме "Окружность"

Итоговый тест по теме «Окружность»

1.Окруж­ность впи­са­на в квад­рат. Най­ди­те пло­щадь квад­ра­та.

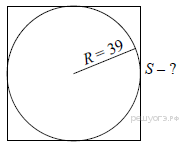
2.Найдите длину окружности, радиус которой равен 8

1. 8 π 2) 16π 3) 32 π 4) 48 π

3. Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те ра­ди­ус окруж­но­сти, если угол между ка­са­тель­ны­ми равен 60°, а рас­сто­я­ние от точки А до точки О равно 8.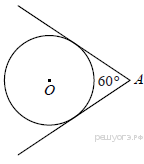

4. 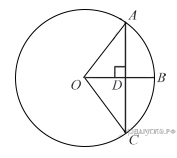Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окруж­но­сти равен 5 см.

Ре­ше­ние.

Най­дем от­ре­зок DO: DO = OB − BD = 5 − 1 = 4. Так как OB пер­пен­ди­ку­ля­рен AC, тре­уголь­ник AOD — пря­мо­уголь­ный. По тео­ре­ме Пи­фа­го­ра имеем: . Тре­уголь­ник AOC — рав­но­бед­рен­ный так как AO = OC = r, тогда AD = DC. Таким об­ра­зом, AC = AD·2 = 6.

Ответ: 6.

Ответ: 6

5. На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что ∠AOB = 66°. Длина мень­шей дуги AB равна 99. Най­ди­те длину боль­шей дуги.

6. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 5. Угол при вер­ши­не, про­ти­во­ле­жа­щий ос­но­ва­нию, равен 120°. Най­ди­те диа­метр окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

7. Точка О – центр окружности, ∠AOB=84°  (см. рисунок). Найдите величину угла ACB (в градусах).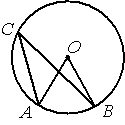

8. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60° . Найдите длину хорды АВ, если радиус окружности равен 8.

9. Прямоугольный тре­уголь­ник с ка­те­та­ми 5 см и 12 см впи­сан в окружность. Чему равен ра­ди­ус этой окружностиРПусть R — ра­ди­ус описанной окружности. Так как окруж­ность описана во­круг прямоугольного треугольника, то ее центр лежит на се­ре­ди­не гипотенузы. Таким образом, ги­по­те­ну­за равна 2R.По тео­ре­ме Пифагора имеем:

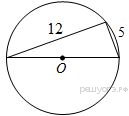
Ответ: 6,5.

Ответ: 6,5

311479

6,5

Источник: ГИА-2013. Математика. Тренировочная работа № 3. (1 вар)

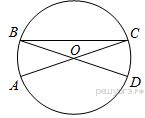
10. AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 23°. Най­ди­те угол AOD. Ответ дайте в градусах.