Исследование алгебраических моделей

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа с.Антоновка

Завитинского района

«Исследование алгебраических моделей»

(Конспект)

Арефина Наталья Ильинична

Учитель информатики и ИКТ, высшая квалификационная категория

Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, - что, следуя этому методу, мы достигнем цели.
Г. Лейбниц

с. Антоновка

2017

Урок информатики в 11 классе на тему «Исследование алгебраических моделей»

Тема: Исследование алгебраических моделей

Класс: 11

Учитель: Арефина Наталья Ильинична

Тип урока: комбинированный

Цель урока:

Создание условий усвоения учащимися особенностей и способов моделирования средствами ИКТ.

Задачи урока:

Образовательные:

1. Систематизировать и расширить представления учащихся о моделях;

2. Научить выбирать способы решения алгебраических уравнений;

3. Научить применять современное программное обеспечение при решении задач алгебраических уравнений.

Развивающие:

1. Повысить познавательный интерес к предмету;

2. Способствовать развитие навыков и способностей критического мышления, направленных на выбор оптимальных решений.

Воспитательные:

1. Воспитывать умение слушать и вступать в диалог;

2. Формировать внимательность и аккуратность в вычислениях.

Планируемые результаты

Личностные:

1. Формирование целостного мировоззрения, соответствующего современному уровню развития науки;

2. Формированиеготовности к самообразованию и самовоспитанию;

3. Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Метапредметные:

1. Владение общепредметными понятиями: объект, система, модель, алгоритм, уравнение, функция и др.;

2. Формирование и развитие компетентности в области использования информационно-коммуникационных технологий.

Познавательные:

1. Умение осуществлять поиск и выделение необходимой информации, в том числе решение рабочих задач с использованием общедоступных источников информации (в учебниках и др. источниках, в т.ч. используя ИКТ);

2. Умение осуществлять постановку и формулирование проблемы;

3. Умение осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;

4. Контроль и оценка процесса и результатов деятельности.

Регулятивные:

1. Целеполагание как постановка учебной задачи;

2. Составление плана и последовательности действий;

3. Работа по плану, нахождение и исправление ошибок, в т.ч. самостоятельно, используя ИКТ.

Коммуникативные:

1. Умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;

2. Управление поведением партнёра — контроль, коррекция, оценка его действий.

3. Коррекция своего мнения под воздействием контраргументов.

Предметные:

1. Развитие основных навыков и умений использования компьютерных устройств;

2. Формирование представления об основных изучаемых понятиях: модель – и их свойства;

3. Формирование навыков и умений безопасного и целесообразного поведения при работе с компьютерными программами.

Организация учебного процесса

Формы работы: Фронтальная, групповая, индивидуальная.

Оборудование урока: Маркерная доска, компьютерная презентация, раздаточный материал, проектор, компьютеры, ПО: свободно распространяемая (GPL) динамическая геометрическая средаGeogebra.

Методы работы: Информационный (словесный), наглядный, иллюстративный, практический.

Структура урока:

1. Организационный момент.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3. Актуализация знаний.

4. Первичное усвоение новых знаний.

5. Первичная проверка понимания.

6. Первичное закрепление.

7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.

8. Информация о домашнем задании, инструктаж по его выполнению.

9. Рефлексия.

1. Ход урока

1. Организационный момент

Цель этапа:

• Включение учащихся в учебную деятельность.

УУД:

Регулятивные:волевая саморегуляция.

Организация учебного процесса на данном этапе:

Учитель: Здравствуйте, ребята! Садитесь.

• Приветствие, фиксация отсутствующих;

• Проверка подготовленности классного помещения.

1. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

Цель этапа:

• Формулировка учащимися темы(преподаватель подводит учащихся к осознанию темы);

• Создание условий для возникновения у учащихся внутренней потребности включения в учебную деятельность.

УУД:

Личностные: стимулирование, самоопределяются, настраиваются на урок.

Познавательные: целеполагание, ставят перед собой цель: «Что я хочу получить сегодня от урока»

Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками.

Регулятивные: перед тем, как начать действовать определяет последовательность действий.

Организация учебного процесса на данном этапе:

Учитель: Эпиграфом к нашему занятию можно считать:

Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, - что, следуя этому методу, мы достигнем цели.

Г. Лейбниц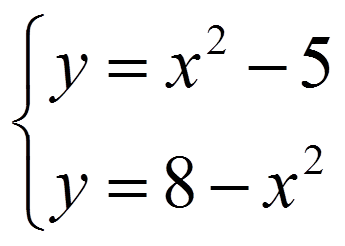

Учитель:Для разминки вспомним алгебру и попробуем решить систему уравнений

Учащиеся:Решение сводится к нахождению корней квадратного уравнения: 2х²-13=0

Учитель:Да, верно. А будет ли просто решить уравнение xlg(x)=1.

Учащиеся:Мы в затруднении.

Учитель: Попробуем решить уравнение графическим способом: Представить уравнение в виде φ(x) = g(x) так, чтобы графики функций y=φ(x) и y=g(x) были известны или достаточно просты для исследования. В одной координатной плоскости построить графики первого и второго уравнения системы и найти координаты точек их пересечения.

Учитель:Как вы думаете, а какова тема нашего сегодняшнего урока?

Учащиеся: Исследование алгебраических моделей.

Учащиеся: Верно. Запишите тему нашего урока «Исследование алгебраических моделей».

1. Актуализация знаний

Цель этапа:

• Включение учащихся в учебную деятельность;

• Актуализация учебного содержания необходимого и достаточного для восприятия нового материала.

УУД:

Личностные: осознание ответственности за общее дело;

Познавательные: поиск и выделение информации, установление причинно-следственных связей, осознанное построение речевого высказывания;

Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками;

Регулятивные: перед тем, как начать действовать определяет последовательность действий.

Организация учебного процесса на данном этапе:

Учитель:Ребята, давайте проверим, какими внимательными вы были на прошлых уроках. Я предлагаю ответить на вопросы теста.

Учащиеся:Учащиеся работают с раздаточным материалом. Приложение 1. Тест «Моделирование как метод познания. Системный подход в моделировании».

Учитель: Итак, работа выполнена. Подведём итоги по образцу. (Проверяют по образцу ).

Учитель: Поднимите руки, кто справился с заданием. Молодцы!

Учитель:Кто не справился с заданиями? В каких заданиях вы допустили ошибку? Давайте вместе их исправим.

Учащиеся:занимаются самопроверкой.

Учитель: И выставим себе отметки за тест.

1 задание – «0,5» балла,

1. Первичное усвоение новых знаний

Цель этапа:

• Включение учащихся в учебную деятельность;

• Актуализация учебного содержания необходимого и достаточного для восприятия нового материала;

• Актуализация мыслительных операций, необходимых для восприятия нового материала;

• Фиксирование определений понятия в виде определений;

• Мотивирование к самостоятельному выполнению учебных действий.

УУД:

Личностные: осознание ответственности за общее дело;

Познавательные: поиск и выделение информации, установление причинно-следственных связей, осознанное построение речевого высказывания;

Коммуникативные: планирование учебного сотрудничества с учителем и одноклассниками;

Регулятивные: перед тем, как начать действовать определяет последовательность действий.

Организация учебного процесса на данном этапе:

Учитель:Итак, ребята, в начале урока вы убедились, что решение некоторых алгебраических уравнений предпочтительней производить графическим способом, иначе говоря – создавать алгебраические модели.

В алгебре формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований алгебраических выражений, позволяющих выразить переменную величину с помощью формулы.

Точные решения существуют только для некоторых уравнений определенного вида (линейные, квадратные, тригонометрические и др.), поэтому для большинства уравнений приходится использовать методы приближенного решения с заданной точностью (графические или численные).

Например, нельзя найти корень уравнения sin(x) = 3х - 2 путем равносильных алгебраических преобразований. Однако такие уравнения можно решать приближенно графическими и численными методами.

Построение графиков функций может использоваться для грубо приближенного решения уравнений. Для уравнений видаf₁(x) = f₂(x),где f₁(x) иf₂(x) — некоторые непрерывные функции, корень (или корни) этого уравнения являются точкой (или точками) пересечения графиков функций.

Графическое решение таких уравнений можно осуществить путем построения интерактивных компьютерных моделей.

Создавать модели мы будем в Geogebra.Geogebra– это свободно распространяемая (GPL) динамическая геометрическая среда.Geogebra предназначена, прежде всего, для решения задач школьного курса геометрии: в ней можно создавать всевозможные конструкции из точек, векторов, отрезков, прямых, строить графики элементарных функций, которые также возможно динамически изменять варьированием некоторого параметра, входящего в уравнение. Кроме того, координаты точек могут быть введены вручную на панели объектов, а уравнения кривых, касательные − в строке ввода при помощи соответствующих команд.

Один из возможностей Geogebra— это наглядное представление графиков функций. Как это сделать? Открываем программу Geogebra. Указываем Алгебра и графики. В нижней части окна программы есть строка ввода формул. Вводим у=3х–2. Нажимаем Enter. Автоматически рисуется график функции. Повторяем с выражением у=sin(x). Точки пересечения графиков функций будут корнями уравнения sin(x) = 3х – 2.

Учитель: Итак, ребята, вы познакомились с методом решения уравнений графическим способом. Вопросы?

1. Первичная проверка понимания.

Цель этапа:

• Проверить правильность и осознанность изученного материала.

УУД:

Познавательные: поиск и выделение информации, установление причинно-следственных связей, конструирование информации в нужной форме;

Коммуникативные: решение учебных проблем возникших в ходе групповой работы;

Регулятивные: перед тем, как начать действовать определяет последовательность действий.

Организация учебного процесса на данном этапе:

Учитель: Итак, ребята, работая в группах за ПК, открываем программу Geogebra. Выполните задание. Вводим линейные, квадратные, тригонометрические уравнения: y=2x; y=x²; y=sinx.

Учитель: Поднимите руки, кто справился с заданием. Молодцы!

Учитель: Кто не справился с заданиями? В каких заданиях вы допустили ошибку? Давайте вместе их исправим.

1. Первичное закрепление.

Цель этапа:

• Закрепить новые знания об алгебраическом моделировании, этапах решения алгебраических уравнениях графическим способом, особенностях динамических геометрических сред и применять полученные знания к решению задач компьютерным способом;

• Мотивирование к самостоятельному выполнению учебных действий

УУД:

Личностные: осознание ответственности за общее дело;

Познавательные: поиск и выделение информации, установление причинно-следственных связей, конструирование информации в нужной форме;

Коммуникативные: решение учебных проблем возникших в ходе индивидуальной работы;

Регулятивные: перед тем, как начать действовать определяет последовательность действий.

Организация учебного процесса на данном этапе:

Учитель: Итак, ребята, работаем индивидуально за ПК, в программе Geogebra. Выполните задание. Задания для практической работы:

1. Решение графическим способом системы уравнений

1. Решение графическим способом системы уравнений
   

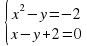
2. Решение графическим способом уравнения:

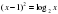
Учитель: Все получат отметки за практическую работу на уроке.

1 задание – «3» балла,

2 задание – «4» балла,

3 задание – «5» баллов.

1. Контроль усвоения, обсуждение допущенных ошибок и их коррекция

Цель этапа:

• Выявить недостатки в знаниях и способах действий учащихся;

• Установить причины выявленных недостатков;

• Откорректировать выявленные пробелы в знаниях и способах действий учащихся в рамках изученной темы.

УУД:

Познавательные:умение осознанно и произвольно строить высказывания;

Коммуникативные: решение учебных проблем возникших в ходе индивидуальной работы;

Регулятивные: контроль и коррекция в форме сравнения способа действия и его результата с заданным эталоном.

Организация учебного процесса на данном этапе:

Учитель: ребята, давайте проверим, что у вас получилось. И выставим себе оценки за практическую работу.

1 задание – «3» балла,

2 задание – «4» балла,

3 задание – «5» баллов.

Учитель: Поднимите руки, кто полностью справился с заданием. Молодцы!

Учитель: Кто не справился с заданиями? В каких заданиях вы допустили ошибку? Давайте, вместе их исправим. Кто заметил повторяющиеся ошибки? Чем они вызваны?

Учитель: Попробуйте выполнить следующее задание: x³ =cosx на интервале от –2,5 до 2,5. Сколько корней имеет уравнение?

1. Информация о домашнем задании, инструктаж по его выполнению

Цель этапа: Концентрация внимания учащихся на изученном материале, постановка задач для продолжения работы дома.

УУД:

Познавательные: умение структурировать знания, оценка процессов и результатов деятельности;

Регулятивные: волевая саморегуляция, осознание того, что уже усвоено и что ещё подлежит усвоению.

Организация учебного процесса на данном этапе:

Учитель: В качестве домашнего задания решите уравнение x³/3=sinx графическим способом. Выберите наиболее удобный для вас способ решения (графический в тетради, в Geogebra или в MSExcel).

1. Рефлексия

Цель этапа: Организовать рефлексию учащихся по поводу своего психоэмоционального состояния, мотивации, своей деятельности, взаимодействия с преподавателем и одноклассниками.

УУД:

Личностные: умение оценивать себя на основе критерия успешности;

Познавательные: умение контролировать и оценивать процесс и результаты деятельности;

Коммуникативные: умение выражать свои мысли, оценивание качества своей и общей учебной деятельности.

Организация учебного процесса на данном этапе:

Учитель: Оцените свое самочувствие на уроке по пятибалльной шкале. Довольны ли Вы итогами этого урока? С чем вы сегодня уйдете с урока? Что вам больше понравилось на сегодняшнем уроке? Достигнута ли цель урока?

Учащиеся: Отвечают, как чувствовали себя, с каким настроением работали, довольны ли собой, комфортно ли было работать в малой группе, какие затруднения были в общении, достиг ли цели учения, какие затруднения возникли, как преодолеть свои учебные проблемы.

Учитель: Какой на ваш взгляд способ построения графика функции более удобен? Почему?

Учащиеся: Отвечают.

1. Асмолов А.Г., Бурменская Г.В., Володарская И.В., Карабанова О.А., Салмина Н.Г., Молчанов С.В.Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий — 2-е изд. — М.: Просвещение, 2011 — 159 с. — (Стандарты второго поколения).

2. Бутурлакина Т.Ю. Методическое пособие по созданию современного урока по ФГОС. – Армавир, 2013 – 60 с.

3. Федеральный государственный образовательный стандарт основного общего образования.– М.: Федеральные Государственные Образовательные Стандарты, 2012

Тест по теме «Моделирование как метод познания.Системный подход в моделировании»

1. Моделирование - это метод познания, состоящий:

   1. в создании моделей

   2. в исследовании моделей

   3. в создании и исследовании моделей

   4. в создании, исследовании и программировании моделей

2. Модель - это новый объект, который:

   1. сохраняет все свойства изучаемого объекта

   2. отражает существенные свойства изучаемого объекта

   3. обладает новыми свойствами

3. При изучении любого объекта можно создать:

   1. единственную модель

   2. несколько различных моделей

   3. точную копию объекта

   4. одну модель, отражающую совокупность признаков

4. Могут ли разные объекты описываться одной и той же моделью?

   1. не могут b. могут c. иногда могут

5. Практически каждый объект состоит из других объектов, т.е. представляет собой:

   1. набор элементов b. систему c. структуру

6. Состояние системы характеризуется ее составом и свойствами элементов, их отношениями и связями между собой, т.е.:

   1. структурой b. системой c. моделью

7. Модели, описывающие состояние системы в определенный момент времени, называются:

   1. статическими информационными моделями

   2. динамическими информационными моделями

8. Модели, описывающие процессы изменения и развития систем, называются:

   1. статическими информационными моделями

   2. динамическими информационными моделями

9. Определите пару объектов, которые находятся в отношении "объект-модель":

   1. компьютер - данные

   2. компьютер - программа

   3. компьютер - алгоритм

   4. компьютер - его функциональная схема

10. Динамической моделью является:

    1. формула химического соединения

    2. формула закона Ома

    3. формула химической реакции

    4. закон всемирного тяготения