Исследование функции по графику.
В.А. Волошина, преподаватель математики
Политехнический колледж «Прогресс»
Илийский район Алматинская облать
В большинстве случаев на уроках математики встречается ситуация: функция задана формулой, требуется исследовать ее свойства и построить график функции. Для укрепления навыков построения графиков функций представляет значительный интерес, другая практическая задача: задан график функции, с помощью которого требуется исследовать свойства функции. Подобные задачи часто встречаются в ходе экспериментальных исследований. Построение графиков при этом осуществляются разными методами. Например: по точкам, найденным экспериментально. В настоящее время при исследовании реальных процессов используют компьютерные технологии для наглядного изображения результатов исследования. Это программа Excel с ее Мастером создания диаграмм.
В 10-11 классах на уроках алгебры и начал анализа часто рассматривается вопрос «Исследование функции и построение ее графика». Графики изучаемых функций представляют собой гладкие кривые, которые наглядно иллюстрируют поведение и свойства функции. Параллельно на уроках информатики учащиеся изучают программу Excel. С помощью Мастера функций учащиеся находят таблицу значений функции и выбирая тип диаграмм стандартные, строят график функций по точечной диаграмме, это удобнее для исследования функции, в других случаях используются диаграмма – график. Уроки математики проводятся в кабинете ИТВ, оборудованном персональными компьютерами. Применение компьютеров позволяет в ряде случаев более наглядно изложить отдельные вопросы программы по математике. Эти уроки могут представлять собой школьную лекцию, лабораторные работы, самостоятельные работы или исследовательские работы
Например: лабораторная работа №1
Тема. Исследование функции по ее графику
Цель. Систематизация и обобщение знаний учащихся этапов исследования функции, умений исследовать функцию по ее графику.
План работы.
Составьте таблицы значений функции, используя программу Excel.
у = 3х2-х3, g = 4х2-х4, z = 5х3-3х5
Постройте графическое изображение функции, используя точечную диаграмму
Исследуйте функцию по ее графическому изображению.
Заполните таблицу.
| 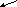 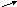 Д(у) Д(у)
| четность | у=0,х=0 | знакопостоянство |
| Max, min | E(y) |
|
|
|
|
|
|
|
|
Учащиеся, реализуя знания о программе Excel, строят и анализируют графики. В данном случае Excel выступает не как объект изучения, а как инструмент познания. За урок учащиеся могут построить и проанализировать большое количество графиков, сделать выводы и получить две оценки – по математике и информатике.
Создание любого графика функции в программе Excel начинается с создания таблицы значений аргумента функции и значения самой функции. Но создание таблицы значений аргумента является основным моментом при построении графика функции. Для создания таблицы значений функции, нужно определить шаг изменения аргумента. Так как многие функции имеют несколько максимумов и минимумов, которые не всегда можно отразить с перового раза, приходиться уже после создания таблицы значений и диаграммы менять шаг изменения аргумента или начальные и конечные значения функции. В результате, определяются, оптимальные параметры диаграммы и график приобретает лучшую наглядность. Таблицу значений аргумента лучше создать учителю и предложить учащимся в лабораторной работе (на уроке нет времени для отбора значений аргумента).
Используя таблицу значений аргумента, учащиеся строят таблицу значений функции с помощью формулы. Необходимо указать учащимся, что функция рассматривается на заданном интервале из области определения функции.
Для построения графика функции запускается Мастер создания диаграмм. Построенная Мастером диаграмма нуждается в форматировании, для этого используется диалоговые окна форматирования.(Рис.1,2,3).
|
|
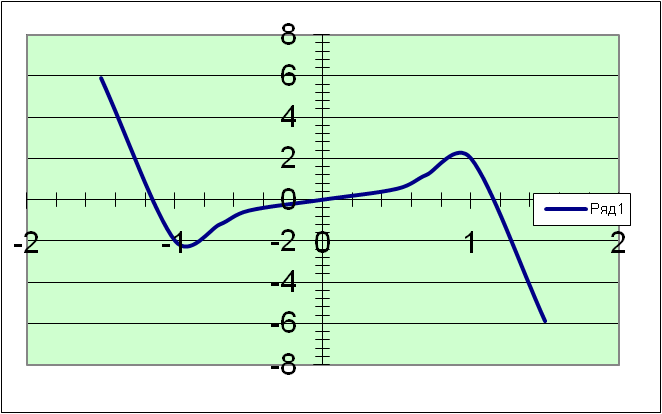
| у =3х2 - х3 |
|
|
|
|
|
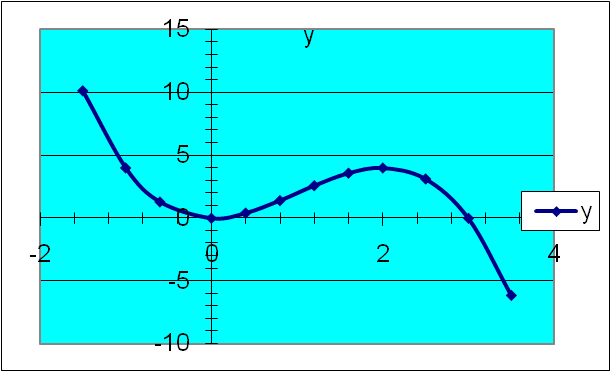
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| х | у |
|
|
|
|
|
|
|
| -1,5 | 10,125 |
|
|
|
|
|
|
|
| -1 | 4 |
|
|
|
|
|
|
|
| -0,6 | 1,296 |
|
|
|
|
|
|
|
| 0 | 0 |
|
|
|
|
|
|
|
| 0,4 | 0,416 |
|
|
|
|
|
|
|
| 0,8 | 1,408 |
|
|
|
|
|
|
|
| 1,2 | 2,592 |
|
|
|
|
|
|
|
| 1,6 | 3,584 |
|
|
|
|
|
|
|
| 2 | 4 |
|
|
|
|
|
|
|
| 2,5 | 3,125 |
|
|
|
|
|
|
|
| 3 | 0 |
|
|
|
|
|
|
|
| 3,5 | -6,125 |
|
|
|
|
|
|
|
|
|
|
|
|
| рис.1 |
|
|
|
|
|
|
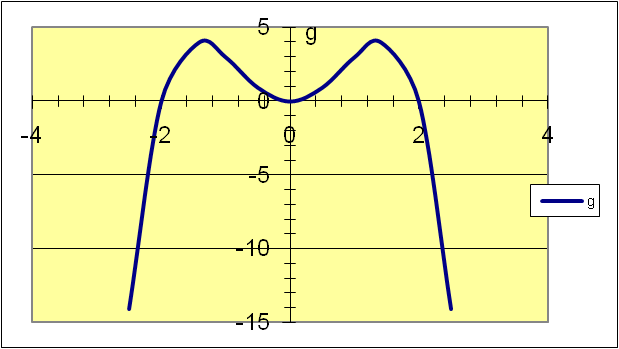
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интерес у учащихся вызывают следующие задания для самостоятельного выполнения.
Самостоятельная работа
Тема. Исследование функции и построение ее графика.
Цель. Сравнение графика функции, построенного с использованием математического аппарата исследования и построенного Мастером диаграмм.
План работы
Используя математический аппарат исследования функции, постройте график функции
у = 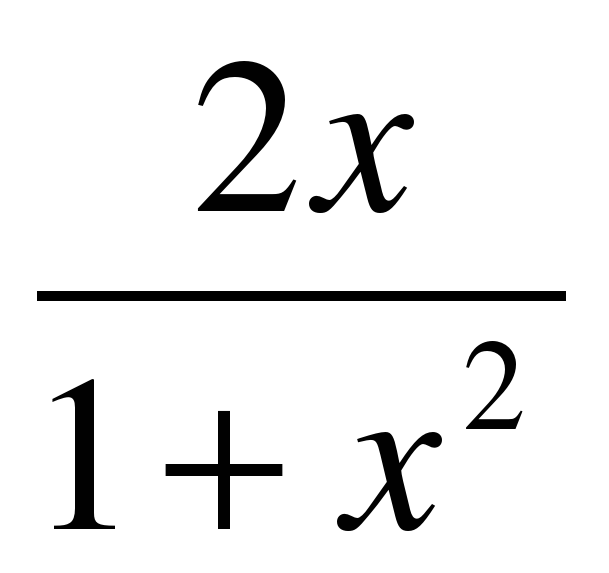 , g =
, g = 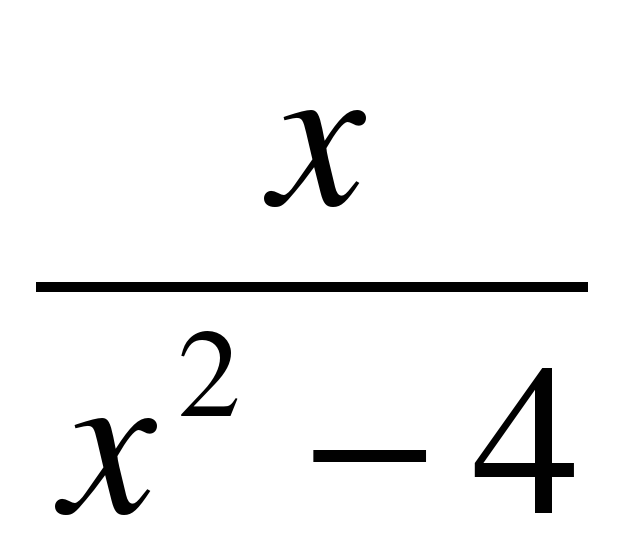
остройте графическое изображение данных функций, используя точечную диаграмму и даграмму график
Сравните графики.
Такую работу может выполнить каждый учащийся: 1) в тетради, проводя исследование функции и строя график функции от руки; 2) на компьютере, используя программу Excel, в отдельной книге, в отдельном файле. Учитель, проверяя тетради выставляет оценку по математике и проверяя файлы учащихся выставляет оценку по информатике.
Можно эту работу выполнить следующим образом. К доске приглашаются ученики, которые исследуют функцию, а затем по результатам исследования строят ее график. Остальные ученики выполняют построение графика в Excel.
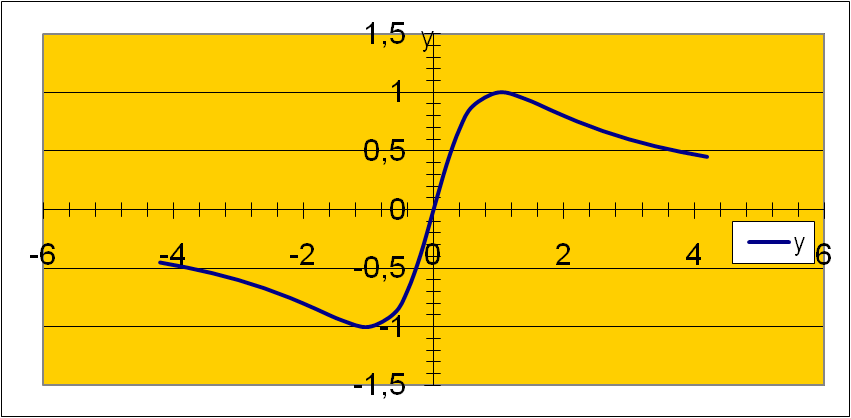
В заключении урока сравниваются графики функций. (Рис. 3; 4.
|
| у=5х3 - 3х5 |
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| у = 2х/ 1+х2 |
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.4 |
|
|
|
|
|
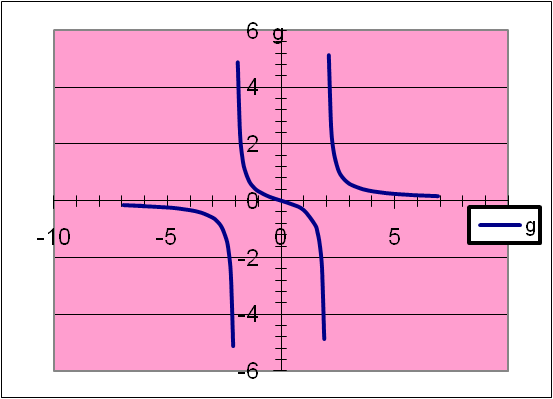
Особый интерес у учащихся вызывает построение графика функции у = 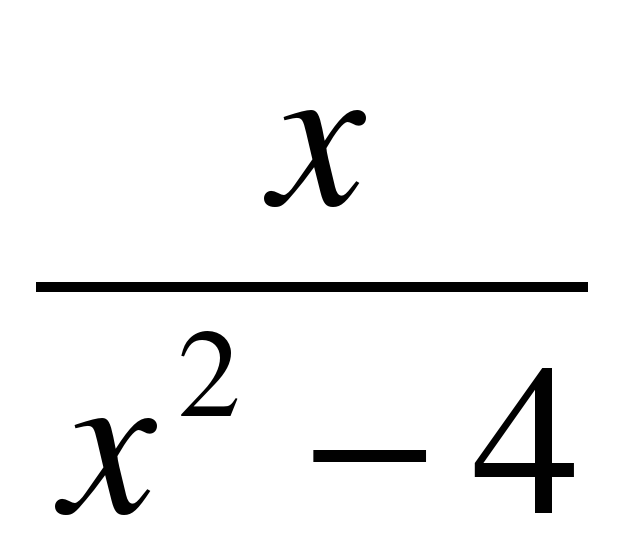 , а именно, наличие вертикальных асимптот. Учитель может на экране продемонстрировать ученикам точки разрыва функции (удалив на графике асимптоты). (Рис.5.)
, а именно, наличие вертикальных асимптот. Учитель может на экране продемонстрировать ученикам точки разрыва функции (удалив на графике асимптоты). (Рис.5.)
|
| у = х / х2 - 4 |
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.5 |
|
|
|
В старших классах изучаются две функции: показательная и логарифмическая, графики которых предлагаются в готовом в виде. Используя программу Excel, ученики могут самостоятельно построить графики этих функций и провести исследоваие функций. Тем более, что навык работы учащихся в программе Excel в 11классе, уже отработан. Например, можно провести следующую лабораторную работу.
Лабораторная работа
Тема. Логарифмическая функция и ее свойства.
План работы.
Составьте таблицы значений функции, используя программу Excel:
y1=log0,1 x, y2=log0,5 x, y3=log0,8 x, y4=log1,5 x, y5=log2 x, y6=log4 x, y7=log10 x
Постройте графическое,иображение логарифмических функций в одной системе координат, используя точечную диаграмму.
Исследуйте функцию по ее изображениям.
Заполните таблицу
| 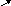    у=loqax у=loqax
| Д(у) | Е(у) | У=0 |
| х1 | х | х ∞ | х 0 |
| а1 |
|
|
|
|
|
|
|
|
| а |
|
|
|
|
|
|
|
|
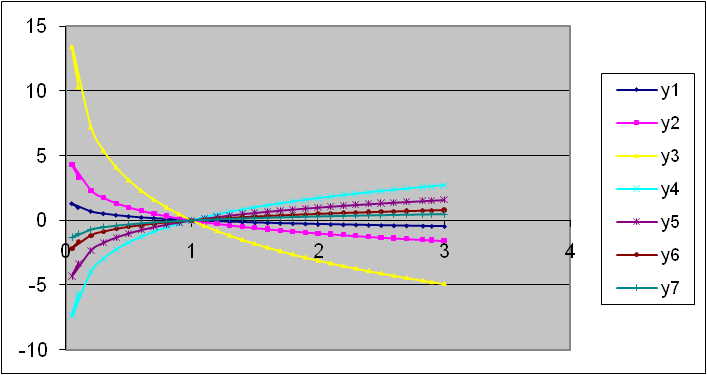
На рисунке 6 показаны результаты лабораторной работы №3.
1 2 3 4 5 6 7
| у1=log0,1 x; | у2=log0,5 х | у3=log0,8 х | у4=log1,5х | у5=log2x; | у6=log4x ; | у7=log10 x |
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.6 |
|
|
|
|
Исследуя функцию, находят определенные характеристики логарифмической функции. На основе этих характеристик учащиеся легко строят от руки эскизы графиков следующих функций в одной системе координат:
у = log3х и у = lgх
у = log 12 и у = log 15 х
у = log4х у = log 14 х,
Не вызывает и затруднение схематическое построение следуюих графиков
у = lg (х- 2)
у = log 12 (х+1)
у = log3х + 2
у = log 13х - 1
у = lg х
Исследование функции по ее графическому изображению позволяет лучше понять логарифм числа, а именно когда логарифм принимает положительные значения, когда отрицательные, сравнивать логарифмы чисел с различным основанием.
Задание. Определите знак логарифма числа:
если а0, а1, N0, N10, N20,
|
| N1 | N1 | N1 N2 | N1 N2 | N1 = N2 |
| а1 | logаN * 0 | logаN * 0 | logа N1* logаN2 | logа N1 * logаN2 | logа N1 * logаN2 |
| а1 | logаN * 0 | logаN * 0 | logа N1 * logаN2 | logа N1 * logаN2 | logа N1 * logаN2 |
Примеры:
1.Определите знак: log24, log1/232, log1/30,7, lg 1/5, lg 10, log5 1, log1/316, log30,9
2.Сравните логарифмы: log23,8 * log24,7; log1/30,15 * log1/30,2; log351 * log349; log0,21,8 * log0,22,1; log26 * 1; log310* log412; log35* log74. Обратите внимание, что сравнение двух последних выражений можно связать со скоростью роста функции, что наглядно показано на рис.6
Аналогично проводится лабораторная работа №4: «Показательная функция и ее свойства».
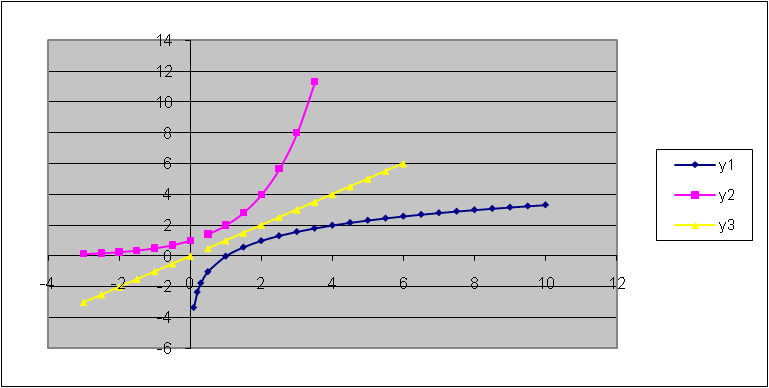
На уроке математики при изучении обратных функций учащимся демонстрируется графики показательной и логарифмической функций, выполненных в одной системе координат (рис7).
|
|
| у=loga x и у=ах , а1 | |
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.7 |
|
|
|
|
Предлагается сравнить основные свойства показательной и логарифмической функций и сделать вывод. Учащиеся должны получить следующие результаты:
Если, а0, а1
| Функция | Д(у) | Е(у) | х = 0 | у = 0 | а1 | 0а1 |
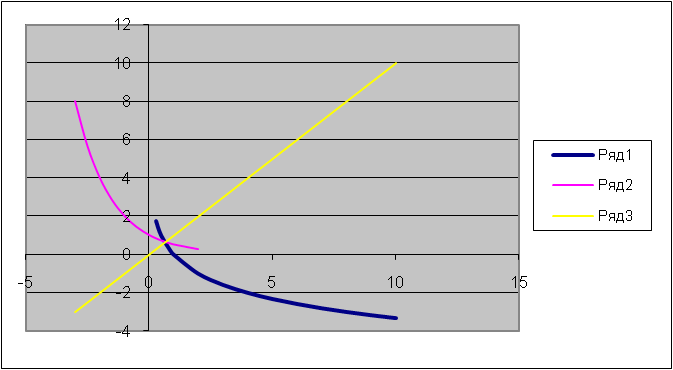
| 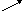 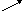 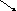 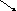 у=ах у=ах
| R | R+ | 1 | нет |
|
|
| у = logах | R+ | R | нет | 1 |
|
|
В
качестве самостоятельного задания для учащихся можно предложить лабораторную работу : Свойства логарифмов.
Цель. Проверка свойств логарифмов чисел, используя программу Электронные таблицы.
План работы.
1.Выполните вычисления в первых строках таблицы без помощи программы Excel.
2.Выполните вычисления в таблицах для любых чисел а0, а≠1, N10 и N20, используя программу Excel.
3.Запишите выводы.
1. Свойство
| а | N1 | N2 | N1* N2 | loqа N1 | loqа N2 | loqа(N1* N2) | loqаN1+loqаN2 | Вывод |
| 2 | 4 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Свойство
| а | N1 | N2 | N1 / N2 | loqа N1 | loqа N2 | loqаN1 / N2 | loqаN1-loqаN2 | Вывод |
| 2 | 4 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3Свойство
| а | p | N | Np | loqа Np | p*loqаN | Вывод |
| 2 | 4 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
4.Свойство
| а | N | loqаN | loqNа | loqаN*loqNа | Вывод |
| 2 | 8 |
|
|
|
|
|
|
|
|
|
|
|
5.Свойство
| а | 1/а | N | loqаN | Loq1/aN | Вывод |
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
Известно, что график показательной функции изображается гладкой линией, к которой в каждой точке можно провести касательную, поэтому естественно предположит, что показательная функция дифференцируема во всех точках области определения функции. Учащиеся могут провести небольшую исследовательскую работу: Взаимное расположение графиков показательной функции и ее производной.
Для вычисления значений показательной функции как всегда используем мастер функции и точечную диаграмму для построения графиков в программе Excel. Для вычисления значений производной целесообразно использовать приближенную формулу
(ах)َ=( ах+Δх- ах):Δх, где Δх стремится к 0
Лабораторная работа №5.
Тема: Взаимное расположение графиков показательной функции и ее производной.
Цель. Определение числа е.
План работы.
1.Составьте таблицы значений функций, используя программу Excel:
у=2х и у′=(2х)′ , g=2,7х и g′=(2,7х)′, z=3х и z′=(3х)′, h=2,71828х и h′=(2,71828х)′.
2.Постройте графическое изображение каждой пары функций в отдельной ситстеме координат с помощью точечной диаграммы.
3.Проведите исследование взаимного расположения графика показательной функции и графика ее производной.
4.Заполните таблицу.
5.Сделайте вывод.
Это может быть групповая работа учащихся на компьютерах (2-3 ученика). Перед учениками ставится проблема: выяснить, когда график показательной функции выше, ниже или совпадает с графиком своей производной? (Рис.8;9).
|
|
| у=loga x и у=ах , 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.8. |
|
|
|
|
|
|
|
|
| у=2х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учащиеся выполняют лабораторную работу и заполняют таблицу, делают вывод.
| а | 2 | 2,7 | 3 | 2,718281828 |
| у=ах |
|
|
|
|
| у=(ах)΄ |
|
|
|
|
| Вывод |
|
|
|
|
При значении а= 2,718281828… учащиеся убеждаются, что график функции у=ах и ее производной практически совпадают. (Рис.10).
|
|
|
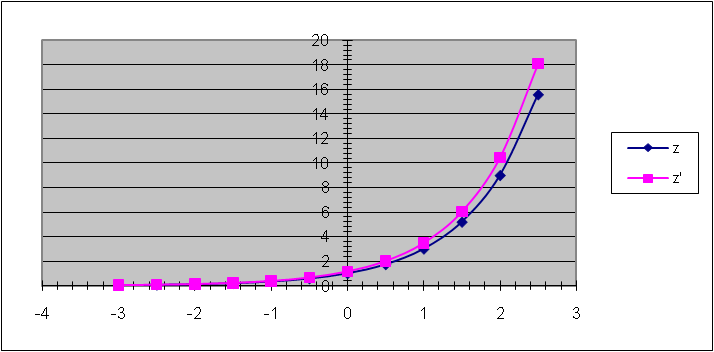
| z=3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.10 |
|
|
|
|
Вводится определение: иррациональное значение а=2,718281828…, при котором совпадают графики функции у=ах и ее производной, обозначают через е и вводятся обозначения у=ех, ехрх, а так же термин «экспонента».
Совпадения графиков у=ех и у=(ех)΄ позволяет сделать вывод, что (ех)΄= ех. (рис 11-12). Тот факт, что при х=0 (ех)΄=1означает: в точке (0;1) тангенс угла наклона касательной к оси абсцисс равен1, а величина угла наклона равна 45˚
Продемонстрируйте на экране рис.1 касательные к кривой у=2х под углом 35˚, к кривой у=3х – под углом в 48˚ и к кривой у=ех под углом 45˚.
Из соотношения (ех)΄=1 при х=0 вытекает, что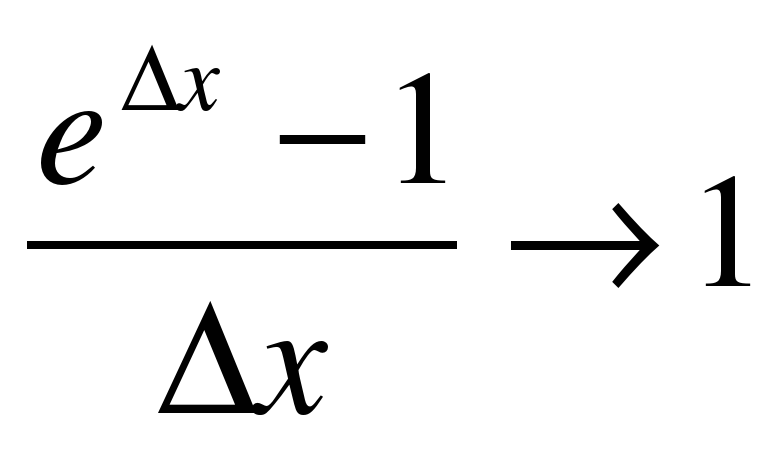 . Это дает возможность доказать теорему о дифференцируемости функции у=ех в каждой точке и доказать равенство (ех)΄= ех.
. Это дает возможность доказать теорему о дифференцируемости функции у=ех в каждой точке и доказать равенство (ех)΄= ех.
|
|
|
|
| x | z | z' |
| -3 | 0,037037 | 0,043009 |
| -2,5 | 0,06415 | 0,074493 |
| -2 | 0,111111 | 0,129026 |
| -1,5 | 0,19245 | 0,223479 |
| -1 | 0,333333 | 0,387077 |
| -0,5 | 0,57735 | 0,670437 |
| 0 | 1 | 1,161232 |
| 0,5 | 1,732051 | 2,011312 |
| 1 | 3 | 3,483695 |
| 1,5 | 5,196152 | 6,033937 |
| 2 | 9 | 10,45109 |
| 2,5 | 15,58846 | 18,10181 |
|
|
| h=2,71828x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| рис.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x | h | h' |
|
| -3 | 0,049787 | 0,052362 |
|
| -2,5 | 0,082085 | 0,08633 |
|
| -2 | 0,135335 | 0,142333 |
|
| -1,5 | 0,22313 | 0,234668 |
|
| -1 | 0,36788 | 0,386902 |
|
| -0,5 | 0,606531 | 0,637894 |
|
| 0 | 1 | 1,051709 |
|
| 0,5 | 1,648721 | 1,733975 |
|
| 1 | 2,71828 | 2,858842 |
|
| 1,5 | 4,481685 | 4,713434 |
|
| 2 | 7,389046 | 7,771138 |
|
| 2,5 | 12,18247 | 12,81244 |
|
ПРИЛОЖЕНИЕ
Лабораторная работа №1
Тема. Исследование функции по ее графику
Цель. Систематизация и обобщение знаний учащихся этапов исследования функции, умений исследовать функцию по ее графику.
План работы.
Составьте таблицы значений функции, используя программу Excel.
у = 3х2-х3, g = 4х2-х4, z = 5х3-3х5
Постройте графическое изображение функции, используя точечную диаграмму
Исследуйте функцию по ее графическому изображению.
Заполните таблицу.
| 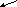 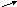 Д(у) Д(у)
| четность | у=0,х=0 | знакопостоянство |
| Max, min | E(y) |
|
|
|
|
|
|
|
|
Самостоятельная работа
Тема. Исследование функции и построение ее графика.
Цель. Сравнение графика функции, построенного с использованием математического аппарата исследования и построенного Мастером диаграмм.
План работы
Используя математический аппарат исследования функции, постройте график функции
у = 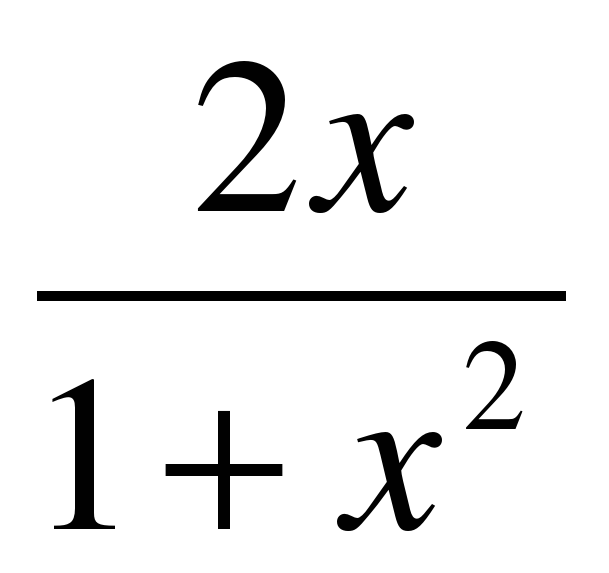 , g =
, g = 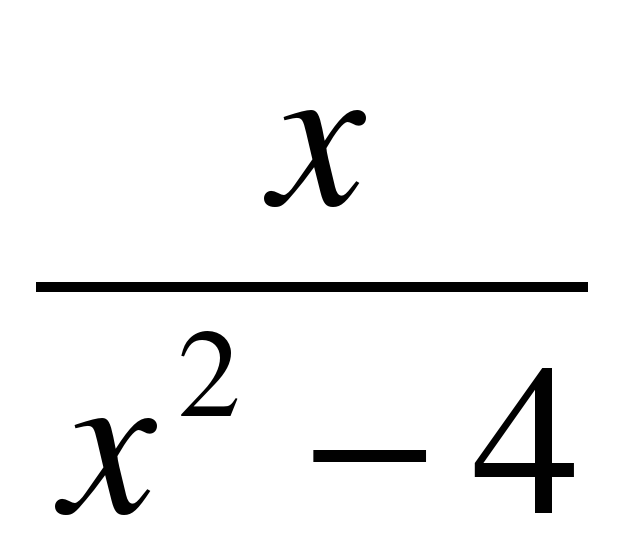
Постройте графическое изображение данных функций, используя точечную диаграмму и диаграмму график
Сравните графики.
Лабораторная работа
Тема. Логарифмическая функция и ее свойства.
План работы.
Составьте таблицы значения функций, используя программу Excel:
y1=log0,1 x, y2=log0,5 x, y3=log0,8 x, y4=log1,5 x, y5=log2 x, y6=log4 x, y7=log10 x
Постройте графическое,иображение логарифмических функций в одной системе координат, используя точечную диаграмму.
Исследуйте функцию по ее изображениям.
Заполните таблицу
| 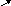  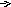  у=loqax у=loqax
| Д(у) | Е(у) | У=0 |
| х1 | х | х ∞ | х 0 |
| а1 |
|
|
|
|
|
|
|
|
| а |
|
|
|
|
|
|
|
|
Задание. Определите знак логарифма числа:
если а0, а1, N0, N10, N20,
|
| N1 | N1 | N1 N2 | N1 N2 | N1 = N2 |
| а1 | logаN * 0 | logаN * 0 | logа N1* logаN2 | logа N1 * logаN2 | logа N1 * logаN2 |
| а1 | logаN * 0 | logаN * 0 | logа N1 * logаN2 | logа N1 * logаN2 | logа N1 * logаN2 |
Примеры:
1.Определите знак: log24, log1/232, log1/30,7, lg 1/5, lg 10, log5 1, log1/316, log30,9
2.Сравните логарифмы: log23,8 * log24,7; log1/30,15 * log1/30,2; log351 * log349; log0,21,8 * log0,22,1; log26 * 1; log310* log412; log35* log74. Обратите внимание, что сравнение двух последних выражений можно связать со скоростью роста функции.
Задание. Сравните свойства показательной и логарифмической функции.
Если, а0, а1
| Функция | Д(у) | Е(у) | х = 0 | у = 0 | а1 | 0а1 |
| 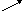    у=ах у=ах
| R | R+ | 1 | нет |
|
|
| у = logах | R+ | R | нет | 1 |
|
|
_____________________________________________________________________
Лабораторная работа №5.
Тема: Взаимное расположение графиков показательной функции и ее производной.
Цель. Определение числа е.
План работы.
1.Составьте таблицы значений функций, используя программу Excel:
у=2х и у′=(2х)′ , g=2,7х и g′=(2,7х)′, z=3х и z′=(3х)′, h=2,71828х и h′=(2,71828х)′.
2.Постройте графическое изображение каждой пары функций в отдельной ситстеме координат с помощью точечной диаграммы.
3.Проведите исследование взаимного расположения графика показательной функции и графика ее производной.
4.Заполните таблицу.
5.Сделайте вывод.
| а | 2 | 2,7 | 3 | 2,718281828 |
| у=ах |
|
|
|
|
| у=(ах)΄ |
|
|
|
|
| Вывод |
|
|
|
|
Лабораторная работа : Свойства логарифмов.
Цель. Проверка свойств логарифмов чисел, используя программу Электронные таблицы.
План работы.
1.Выполните вычисления в первых строках таблицы без помощи программы Excel.
2.Выполните вычисления в таблицах для любых чисел а0, а≠1, N10 и N20, используя программу Excel.
3.Запишите выводы.
1. Свойство
| а | N1 | N2 | N1* N2 | loqа N1 | loqа N2 | loqа(N1* N2) | loqаN1+loqаN2 | Вывод |
| 2 | 4 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Свойство
| а | N1 | N2 | N1 / N2 | loqа N1 | loqа N2 | loqаN1 / N2 | loqаN1-loqаN2 | Вывод |
| 2 | 4 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3Свойство
| а | p | N | Np | loqа Np | p*loqаN | Вывод |
| 2 | 4 | 8 |
|
|
|
|
|
|
|
|
|
|
|
|
4.Свойство
| а | N | loqаN | loqNа | loqаN*loqNа | Вывод |
| 2 | 8 |
|
|
|
|
|
|
|
|
|
|
|
5.Свойство
| а | 1/а | N | loqаN | Loq1/aN | Вывод |
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
Исследуя функцию, находят определенные характеристики логарифмической функции. На основе этих характеристик постройте от руки эскизы графиков следующих функций в одной системе координат:
у = log3х и у = lgх
у = log 12 и у = log 15 х
у = log4х у = log 14 х,
Не вызывает и затруднение схематическое построение следуюих графиков
у = lg (х- 2)
у = log 12 (х+1)
у = log3х + 2
у = log 13х - 1
у = lg х


 Получите свидетельство
Получите свидетельство Вход
Вход


 Д(у)
Д(у)





 у=loqax
у=loqax













 Исследование функции по графику (методический материал) (0.62 MB)
Исследование функции по графику (методический материал) (0.62 MB)
 0
0 1138
1138 142
142 Нравится
0
Нравится
0










