МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЁЖНОЙ ПОЛИТИКИ НИЖЕГОРОДСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СЕМЕНОВСКИЙ ИНДУСТРИАЛЬНО-ХУДОЖЕСТВЕННЫЙ ТЕХНИКУМ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ИСПОЛЬЗОВАНИЕ ОФИСНЫХ ПРОГРАММ НА УРОКАХ МАТЕМАТИКИ
Разработчик: Кочнева О.А.
2022
Пояснительная записка 3
Использование офисных программ на уроках математики для студентов 4
ОУД.04 Математика 4
Логарифм. Логарифмическая функция 4
Вычисление значений тригонометрических функций 5
Элементы комбинаторики 7
Дискретная случайная величина и ее числовые характеристики 8
Построение графиков функций 9
Построение сечений тетраэдра и параллелепипеда 10
Многоугольники 12
Прямоугольный параллелепипед, куб 13
ЕН.01 Математика 15
Интервальный ряд распределения, его статистические характеристики 15
Действия с матрицами 15
ЕН.02 Дискретная математика 17
Логические операции 17
Построение полинома Жегалкина 17
Использование офисных программ на уроках математики для преподавателей 21
Заключение 24
Литература и источники 25
Перед каждым из преподавателей время от времени встает проблема повышения мотивации к обучению. Все мы стараемся заинтересовать обучающихся своим предметом. Кроме того, для преподавателя очень важно, чтобы студент ощущал себя успешным. Ну и каждому, наверное, хочется оптимизировать свой труд, меньше времени тратить на однотипные действия.
В своей статье А.А. Морозкина отмечает, что «информационные технологии широко, интенсивно и эффективно используются человеком во всех сферах деятельности. Для миллионов людей компьютер превратился в привычный атрибут повседневной жизни, стал незаменимым помощником в учебе, в работе и отдыхе. Он избавил человека от рутинного труда, упростил поиск и получение необходимой и своевременной информации, общение между людьми, ускорил принятие решений»
Гайнатуллина М.В., учитель математики и информатики, также рассуждает над вопросом «как сделать, чтобы применение компьютера стало естественной потребностью, не вызывало различных дополнительных проблем, чтобы компьютер экономил время учителя, разгружал его» и предлагает применять различные возможности электронных таблиц, стандартно включенных в пакет офисных программ, для оптимизации уроков алгебры.
Отдельно хотелось бы отметить, что в настоящее время к студентам всё чаще предъявляются требования по оформлению различных работ, в том числе содержащих расчеты и графики, в электронном виде. Однако, несмотря на то, что на уроках информатики обучающиеся оформляют текстовые документы, выполняют расчеты в электронных таблицах, у них не всегда формируются межпредметные связи: некоторые студенты не применяют полученные знания на других дисциплинах.
Всё это привело к мысли, что на занятиях математики имеет смысл организовать работу с использованием компьютера и офисных программ. Чаще всего сначала на уроке математики студенты знакомятся с новым понятием, рассматриваются его свойства и допустимые операции, затем действия отрабатываются вручную. И уже потом рассматривается возможность автоматизировать процесс вычислений, например, с помощью электронных таблиц. Ниже предложены фрагменты таких занятий по различным темам.
На одном из занятий по данной теме студентам предлагается выполнить следующее практическое задание:
Задание 1. Вычислите с помощью калькулятора с точностью до 0,01. Занесите результаты вычислений в таблицу.
| Пример |
|
|
|
|
| Ответ |
|
|
|
|
Задание 2. Придумайте свой пример на вычисление логарифма, напечатайте его и решите.
Ответ:
Задание 3. Напечатайте и отформатируйте текст, чтобы он примерно соответствовал образцу:

Задание 4. Экономическая функция объема производства продукции Q (в тоннах) зависит от цены Р (в условных единицах) согласно закону: 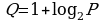 и может принимать только положительные значения. Определите объем производства продукции (в тоннах) при указанных ценах. Результаты вычислений занесите в таблицу.
и может принимать только положительные значения. Определите объем производства продукции (в тоннах) при указанных ценах. Результаты вычислений занесите в таблицу.
| Цена (Р), у.е. | 1 | 2 | 4 | 8 | 16 |
| Объем производства (Q), т |
|
|
|
|
|
Задание 5. Откройте в программе Paint файл Предложение. По полученным результатам вычислений постройте график функции Q(P). Скопируйте его и поместите под текстом данного задания.
Задание 6. По графику приблизительно определите:
объем производства (в тоннах) при цене Р = 10 у.е.
Ответ:
при какой цене (в у.е.) объем производства составит 4,5 тонны.
Ответ:
В процессе выполнения работы студенты закрепляют умения выполнять вычисления с помощью калькулятора, оформлять текст в текстовом редакторе, вычислять логарифмы устно по определению, строить график логарифмической функции и «читать» его. В дальнейшем задания 4 и 5 можно использовать как мотивационные при изучении темы «Построение графиков в Excel»
На одном из уроков по разделу «Тригонометрия» студентам предлагается с помощью калькулятора и электронных таблиц вычислить значения тригонометрических выражений.
Вычислите, используя калькулятор:
| Пример | Ответ | Балл | |
| максимальный | полученный | ||
| cos 250 |
| 1 |
|
|
|
| 2 |
|
Вычисляет ли калькулятор на Вашем телефоне значения тригонометрических выражений?
| Да | Балл | Нет | |||
| Макс. | Получ. | ||||
| Узнайте, в каких единицах измерения (градусах или радианах) нужно вводить число | 1 |
| Найдите в интернете он-лайн калькулятор для вычисления значений тригонометрических выражений. | ||
| Ответ: | Ответ (ссылка): | ||||
| Есть ли кнопки для перевода чисел из радиан в градусы и из градусов в радианы? Если да, как они называются? | 1 |
| Есть ли кнопки для перевода чисел из радиан в градусы и из градусов в радианы? Если да, как они называются? | ||
| Ответ: | Ответ: | ||||
| Вычислите, используя свой калькулятор: | 2 |
| Вычислите, используя он-лайн калькулятор: | ||
| sin 430 | Ответ: | sin 430 | Ответ: | ||
|
| Ответ: | 2 |
|
| Ответ: |
Откройте электронную таблицу Тригонометрия. Напечатайте свои фамилии и инициалы.
В строке «Пример» вычислите 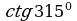 :
:
| Задание | Балл |
| В ячейку В3 (число в градусах) внесите 315. | 0,5 |
| В ячейку С3 введите формулу для перевода числа из градусов в радианы: напечатайте знак «равно», затем слово РАДИАНЫ, откройте скобку, щелкните по ячейке В3, закройте скобку, нажмите Enter. | 0,5 |
| В ячейке D3 напечатайте слово тангенс (т.к. в Excel нет функции, вычисляющей котангенс числа). | 0,5 |
| В ячейку Е3 введите формулу для вычисления тангенса числа, выраженного в радианах: напечатайте знак «равно», затем слово TAN, откройте скобку, щелкните по ячейке C3, закройте скобку, нажмите Enter. | 0,5 |
| В ячейке F3 напечатайте слово котангенс. | 0,5 |
| В ячейке G3 введите формулу для вычисления котангенса числа по его тангенсу: напечатайте знак «равно», затем 1, знак деления (косая черта на цифровой клавиатуре), щелкните по ячейке Е3, нажмите Enter. | 0,5 |
Внесите в таблицу данные и формулы для вычисления значения выражений (последние два столбца заполнять не нужно):
| Пример | Балл |
| sin 300 | 2 |
|
| 2 |
|
| 2 |
В данной таблице выполните вычисления:
| Пример | Балл |
| Вычислите синус и косинус 3 радиан | 2 |
| Проверьте с помощью основного тригонометрического тождества, что сумма их квадратов равна 1. | 2 |
В данной таблице вычислите tg 500 двумя способами:
| Пример | Балл |
| С помощью соответствующей функции | 2 |
| По определению | 5 |
Сохраните изменения в данном документе и электронной таблице.
Для работы в электронных таблицах студентам предлагается следующая заготовка:
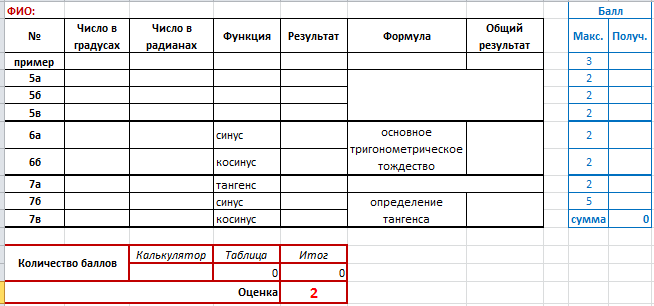
При проверке преподаватель вносит полученные баллы, при этом оценка выставляется автоматически. В процессе выполнения предложенных заданий обучающиеся продолжают формировать умения выполнять вычисления с помощью калькулятора и электронных таблиц. Довольно часто у студентов вызывает затруднение использование формул с функциями в электронных таблицах, поэтому в задании даётся подробная инструкция.
Очень удобно использовать электронные таблицы при изучении элементов теории вероятностей и математической статистики. Ниже приведено практическое задание по теме «Элементы комбинаторики».
Загрузите программу Word.
Оформите таблицу по образцу:
| Все элементы используются? | ||
| нет | да | |
| Порядок важен? | перестановки | |
| нет | да | |
| сочетания | размещения | |
Напечатайте формулировку задачи:
Однажды Коля пошел на рыбалку и поймал щуку, карася, плотвичку, ерша, леща и уклейку. А потом решил, что обязательно должен угостить своего кота Мурзика. Сколькими способами можно накормить кота двумя рыбами?
Определите, о каком понятии идет речь, для этого закрасьте нужные клетки созданной таблицы.
Напечатайте формулу, по которой будете выполнять вычисления.
Выполните вычисления, используя калькулятор.
Запишите ответ к задаче.
Перейдите на отдельную страницу: Вставка→ Разрыв страницы.
Скопируйте созданную таблицу, задайте для всех ячеек тип заливки «Нет цвета».
Напечатайте формулировку задачи:
Пусть даны n цифр. Сколько k-значных чисел, в которых все цифры разные, можно из них составить?
Определите, о каком понятии идет речь, для этого закрасьте нужные клетки второй таблицы.
Загрузите программу Excel, оформите в ней таблицу:
| № | n | k | Результат |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
Заполните 2 и 3 столбцы произвольно, в четвертом столбце с помощью соответствующей функции выполните вычисления.
Скопируйте полученную таблицу с результатами вычислений в текущий документ.
Найдите в интернете изображение по теме одной из задач. Скопируйте его и вставьте в документ справа от текста соответствующей задачи.
Добавьте в документ титульную страницу: Вставка→ Титульная страница. Введите название документа – «Решение комбинаторных задач»; авторов документа – ваши фамилии и инициалы.
При выполнении данных заданий студенты продолжают формировать умения определять, о каком понятии идет речь в задаче, выбирать нужную формулу для вычисления, а также аккуратно оформлять документ, содержащий таблицы и формулы. Вторая задача сформулирована таким образом, чтобы обучающиеся видели возможности автоматизации расчетов в программе Excel.
При изучении темы «Закон распределения дискретной случайной величины» сначала студенты вручную по формуле Бернулли несколько раз вычисляют вероятность. К этому времени они уже знакомы с электронными таблицами. Приходит идея, что вычисления можно автоматизировать. Фронтально рассматривается эта возможность: в Excel оформляется таблица с исходными данными и копируемой формулой для расчетов. Далее студенты знакомятся со встроенной функцией, которая вычисляет вероятность по формуле Бернулли, а затем самостоятельно решают задачи по вариантам. Один приведен ниже:
В своей папке создайте документ ДСВ, напечатайте задачу.
В кастинге на конкурс красоты участвуют 9 блондинок и 6 брюнеток. На конкурс выбираются 6 человек. Составьте закон распределения числа блондинок, выбранных на конкурс. Вычислите математическое ожидание, дисперсию и среднее квадратичное отклонение числа блондинок, выбранных на конкурс. Постройте многоугольник распределения.
В своей папке создайте лист Excel ДСВ, выполните расчеты (для вычисления вероятностей примените ОДИН ЛЮБОЙ СПОСОБ).
Скопируйте результаты вычислений в документ, сделав пояснения.
В Excel постройте многоугольник распределения; скопируйте его в документ.
Сохраните изменения в обоих файлах.
В результате получается примерно такая таблица:
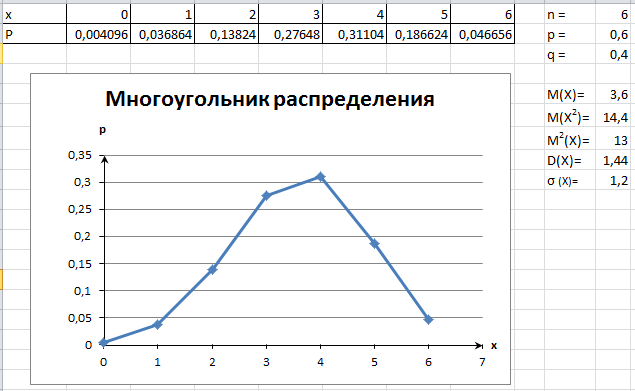
При изучении темы «Построение графиков функций» важно не только сформировать умения исследовать функцию методами дифференциального исчисления, но и «читать» построенный график. С этой целью студентам предлагается следующее практическое задание, выполняемое на компьютере.
Задание: вычислить значения функции 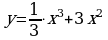 на отрезке [-8; 4] с шагом 1, построить график функции и проанализировать его.
на отрезке [-8; 4] с шагом 1, построить график функции и проанализировать его.
Ход работы:
В своей папке создайте новый лист MS Excel, который назовите График.
В ячейке А1 напечатайте х, в ячейке В1 – у.
В ячейке А2 напечатайте первое значение аргумента -8; в ячейке А3 - второе значение аргумента -7;
Выделите ячейки А2 и А3 и выполните протягивание вниз пока не получите число 4.
В ячейку В2 введите формулу для вычисления значения функции 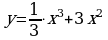 .
.
С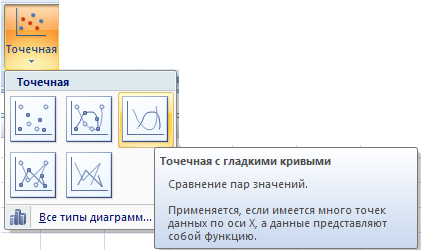 копируйте формулу вниз для остальных значений переменной х.
копируйте формулу вниз для остальных значений переменной х.
Выделите результаты вычислений в столбце В, выполните округление до одного знака после запятой с помощью кнопки ![]() на вкладке Главная.
на вкладке Главная.
Выделите всю полученную таблицу, на вкладке Вставка щелкните по кнопке Точечная и выберите точечную диаграмму с гладкими кривыми.
Для полученной диаграммы на вкладке Конструктор выберите Макет 10.
Скопируйте диаграмму в данный документ.
По графику и имеющейся таблице данных определите:
Точку максимума: х1 =
Точку минимума: х2 =
Интервал(ы), на которых функция возрастает: х (
Интервал(ы), на которых функция убывает: х (
Наибольшее значение функции на отрезке [-8; 4]: yнб =
Наименьшее значение функции на отрезке [-8; 4]: yнм =
Офисные программы дают возможность красиво и аккуратно оформлять текстовые документы, содержащие таблицы и иллюстрации. До этого момента студенты вручную на занятиях и дома строили сечения тетраэдра и параллелепипеда. Это занятие направлено на коррекцию и закрепление знаний и умений построения сечений, оформления текстового документа, содержащего различные объекты. Рисунок создается с помощью графического редактора Paint, а затем копируется в документ.
В начале занятия организуется актуализация знаний. Преподаватель задает вопросы, а студенты отвечают на них и демонстрируют ответ на экране. При технической возможности используется интерактивная доска.
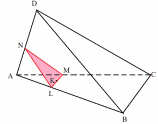
Обучающимся предлагается рассмотреть следующую задачу: постройте сечение тетраэдра DABC плоскостью, проходящей через внутреннюю точку К основания тетраэдра параллельно боковой грани DBC.
Как в документе организовать пространство, чтобы аккуратно рядом записать, что дано, построить чертеж и записать ход его построения? Создайте таблицу, содержащую 3 столбца и 2 строки.
Какие условия даны? Как напечатать символы, которых нет на клавиатуре? Заполните первый столбец таблицы (дано).
Какая программа позволяет создавать изображения? Загрузите программу Paint, постройте тетраэдр.
Как сделать подписи в программе Paint? Подпишите вершины тетраэдра, отметьте точку К.
Известно, что секущая плоскость параллельна плоскости DBC. Какую прямую нужно провести, чтобы начать построение сечения? Через точку К в плоскости АВС постройте прямую ML, параллельную прямой ВС. Далее происходит построение остальных отрезков сечения, делаются записи шагов построения сечения в последнем столбце таблицы.
Как применить заливку в программе Paint? Закрасьте построенное сечение.
Как скопировать рисунок в документ? Выделите полученный рисунок и скопируйте его во второй столбец таблицы. В результате получается такой документ:
| Дано | Рисунок | Решение |
| Тетраэдр DABC, К ABC, K γ γ || DBC
Построить сечение плоскостью γ |
| K ML, ML || BC, MN || CD NL || BD
MNL - сечение. |
Далее студентам предлагается самостоятельно по вариантам в соответствии с заданием решить 2 задачи на построение сечений. Ниже предложен один из вариантов задания.
Вариант 1
В своей папке создайте новый документ, который назовите «Сечения».
Перепечатайте текст задачи.
Создайте таблицу, содержащую 3 столбца и 2 строки.
В первой строке напечатайте заголовки столбцов: дано, рисунок, решение.
В первой ячейке второго столбца с помощью математических символов напечатайте, что дано.
Загрузите программу Paint, постройте многогранник, указанный в задаче, подпишите его вершины, отметьте точки в соответствии с условием задачи, постройте сечение, примените к нему заливку.
Сохраните рисунок, созданный в программе Paint, в свою папку.
Скопируйте многогранник с сечением в документ (во вторую ячейку второй строки).
В последней ячейке второй строки математическими символами запишите ход построения сечения.
А налогично оформите решение второй задачи.
налогично оформите решение второй задачи.
Задача 1. Постройте сечение параллелепипеда MBCDEFGH плоскостью, проходящей через точки M, P, K.
Задача 2. Постройте сечение тетраэдра DABC плоскостью, проходящей через ребро основания ВС и середину противоположного ребра.
До изучения раздела «Многогранники» важно провести актуализацию и напомнить обучающимся основные свойства треугольников и четырехугольников, формулы для нахождения их площадей и периметров, теорему Пифагора. Здесь опять же можно провести занятие с использованием офисных программ и предложить студентам выполнить задание с помощью электронных таблиц.
В начале занятия преподаватель демонстрирует на экране, а студенты обсуждают и параллельно с ним выполняют на компьютерах следующие действия:
В своей папке создайте новый лист Excel, который назовите Многоугольники.
Выделите 10 столбцов, настройте их ширину так, чтобы получилось клетчатое поле.
Нарисуйте ромб, примените прозрачную заливку.
Какие элементы ромба нужно знать, чтобы вычислить его площадь? Изобразите диагонали ромба, посчитайте по клеткам их длины, справа запишите результат, вычислите с помощью формулы площадь ромба.
Что такое периметр многоугольника? Как найти сторону ромба? Вычислите сторону ромба по теореме Пифагора, найти периметр.
После выполнения этих действий будет получен примерно такой результат:
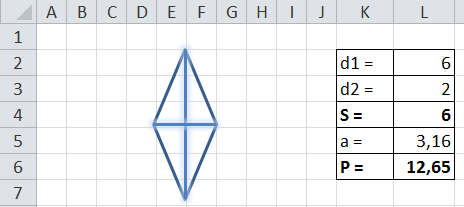
Далее аналогичные действия студентам предлагается выполнить самостоятельно на оценку:
В файле Многоугольники на текущем листе ниже постройте любой вид каждого из указанных многоугольников:
Прямоугольник.
Треугольник.
Трапецию.
Параллелограмм.
Справа запишите, чему равны их элементы, необходимые для вычисления площади.
Вычислите площадь каждого многоугольника.
Найдите все стороны каждого многоугольника (с помощью теоремы Пифагора).
Вычислите периметр каждого многоугольника.
Критерии оценки
За каждый правильно построенный многоугольник – 1 балл (итого 4).
За каждую правильно вычисленную площадь – 1 балл (итого 4).
За правильно найденные неизвестные стороны – 1 балл для каждого многоугольника кроме прямоугольника (итого 3)
За каждый правильно найденный периметр – 1 балл (итого 4).
| Отлично | Хорошо | Удовлетворительно | Неудовлетворительно |
| 14-15 баллов | 10-13 баллов | 7-9 баллов | 0-6 баллов |
При изучении темы «Прямоугольный параллелепипед, куб» на этапе актуализации студентам предлагается заполнение таблицы. В процессе выполнения задания студенты повторяют изученный материал по геометрии и продолжают формировать умения печатать формулы в текстовом редакторе, работать с изображениями фигур и надписями.
Заполните пропуски в таблице. Значения a, b, c берите в соответствии с вариантом.
| Изобразите прямоугольный параллелепипед. Параллелепипед называется прямоугольным, если его боковые ребра ___________________ к основанию, а основания представляют собой _________________________. Измерениями прямоугольного параллелепипеда называются __________________________________, ____________________________________________. Отметьте их на чертеже буквами а, b, c. |
|
| Диагональю прямоугольного параллелепипеда называется отрезок, соединяющий ______________________________________________________________________. Изобразите диагональ параллелепипеда, обозначьте ее d. | |
| Запишите свойство диагонали прямоугольного параллелепипеда формулой. |
|
| Измерения прямоугольного параллелепипеда равны а, b, c. Найдите его диагональ. |
|
| Запишите формулу площади поверхности прямой призмы. |
|
| Запишите формулу площади поверхности прямоугольного параллелепипеда, используя сделанные обозначения. |
|
| Измерения прямоугольного параллелепипеда равны а, b, c. Найдите площадь поверхности прямоугольного параллелепипеда |
|
| Запишите формулу объема призмы. |
|
| Запишите формулу объема прямоугольного параллелепипеда, используя сделанные обозначения. |
|
| Измерения прямоугольного параллелепипеда равны а, b, c. Найдите его объем |
|
| Кубом называется прямоугольный параллелепипед, у которого ___________________________________. Изобразите куб. Гранями куба являются ________________________ ____________________________________________. Обозначьте ребро куба а. |
|
| Запишите формулу площади поверхности куба. |
|
| Найдите площадь поверхности куба, если его ребро равно а. |
|
| Запишите формулу объема куба. |
|
| Найдите объем куба, если его ребро равно а. |
|
| Запишите свойство диагонали куба формулой. |
|
Поскольку вычисления однотипны, студентам предлагается 8 вариантов. Преподавателю же для проверки поможет электронная таблица, в которой расчеты выполнены для первого варианта, а затем для остальных вариантов формулы скопированы:
| вариант | a | b | c | d | Sпар | Vпар | Sкуб | Vкуб |
| 1 | 2 | 2 | 1 | 3 | 16 | 4 | 24 | 8 |
| 2 | 2 | 3 | 6 | 7 | 72 | 36 | 24 | 8 |
| 3 | 4 | 8 | 1 | 9 | 88 | 32 | 96 | 64 |
| 4 | 4 | 4 | 7 | 9 | 144 | 112 | 96 | 64 |
| 5 | 2 | 6 | 9 | 11 | 168 | 108 | 24 | 8 |
| 6 | 6 | 3 | 2 | 7 | 72 | 36 | 216 | 216 |
| 7 | 6 | 6 | 7 | 11 | 240 | 252 | 216 | 216 |
| 8 | 2 | 10 | 11 | 15 | 304 | 220 | 24 | 8 |
На втором курсе электронные таблицы используются при изучении элементов математической статистики и действий с матрицами.
Интервальный ряд распределения, его статистические характеристикиПри изучении темы «Интервальный ряд распределения, его статистические характеристики» сначала студенты вручную строят его, занося данные в таблицу. И снова возникает идея, что для автоматизации повторяющихся действий и быстрого и аккуратного оформления таблицы удобно использовать программу Excel. На уроке сначала рассматривается общая задача, параллельно с преподавателем студенты отрабатывают алгоритм построения интервального ряда в электронных таблицах с помощью встроенных функций, затем уже обучающиеся самостоятельно на компьютерах решают задачу в соответствии с вариантом. Ниже приведен один из них:
В таблице указаны данные о времени, которое затрачивают на дорогу до техникума в минутах случайно выбранные студенты:
| 50 | 35 | 18 | 35 | 36 | 30 | 40 |
| 22 | 20 | 35 | 32 | 32 | 78 | 32 |
| 38 | 38 | 20 | 20 | 23 | 17 | 38 |
| 25 | 38 | 18 | 47 | 20 | 32 | 32 |
| 64 | 12 | 90 | 76 | 45 | 43 | 16 |
Постройте интервальный ряд, для этого определите:
количество элементов ряда;
количество интервалов;
ширину шага интервала;
нижние и верхние границы интервалов;
количество элементов в интервалах (абсолютные частоты) (ni);
частости (относительные частоты) интервалов (wi);
накопленные частоты (si).
Найдите среднее арифметическое, моду и медиану интервального ряда.
Как и в выше рассмотренных примерах использования электронных таблиц сначала студенты знакомятся с понятием матрицы, операциями над матрицами, тренируются выполнять их вручную. У некоторых возникает идея, что можно использовать электронные таблицы для автоматизации расчетов; со сложением, вычитанием и умножением на число проблем не возникает, а для остальных действий использование формул для вычислений кажется довольно сложным. На соответствующем занятии преподаватель знакомит студентов со встроенными функциями, которые позволяют транспонировать, умножать матрицы, находить определитель и обратную матрицу. Вычисления становятся простыми и для больших матриц, поэтому во время решения практического задания по этой теме внимание уделяется, в том числе аккуратному оформлению вычислений.
Работа, которая выполняется параллельно вместе со студентами, выглядит примерно следующим образом:
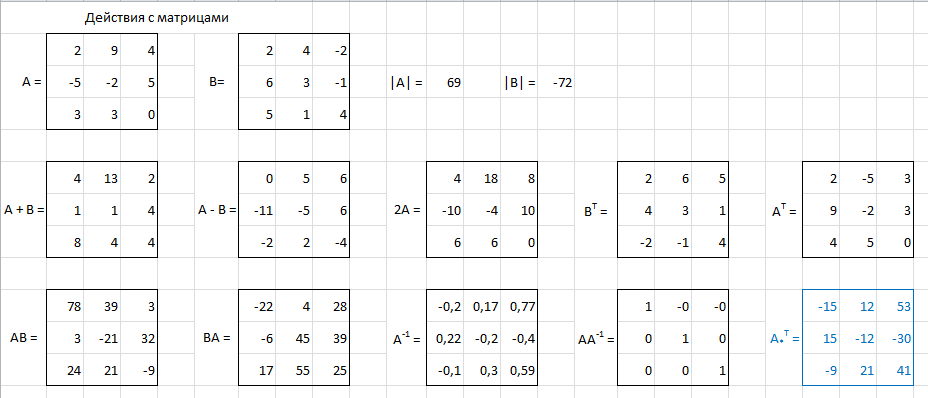
Задание:
Составьте две матрицы четвертого порядка.
Найдите А + 2В;
Найдите АТ;
Найдите АхВ;
Найдите |А|;
Найдите А-1;
Выполните проверку.
Данная дисциплина изучается студентами специальности «Сетевое и системное администрирование».
Логические операции|
|
|
|
|
|
|
|
|
|
| А | 1 | не А | 0 | А×В + не А |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| |
|
|
| 1 | А×В |
| 1 |
| |
|
| В | 1 | 1 |
|
| ||
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
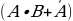 таблица будет выглядеть следующим образом. При изменении исходных данных, происходит автоматический пересчет. В качестве дополнительного задания студентам можно предложить с помощью условного форматирования сделать так, чтобы 0 был одного цвета, а 1 другого. Построение полинома Жегалкина
таблица будет выглядеть следующим образом. При изменении исходных данных, происходит автоматический пересчет. В качестве дополнительного задания студентам можно предложить с помощью условного форматирования сделать так, чтобы 0 был одного цвета, а 1 другого. Построение полинома Жегалкина Существует несколько методов построения полинома Жегалкина; для 2 и 3 переменных это сделать несложно. В процессе построения много раз повторяются одни и те же действия. И снова приходит на ум, что можно автоматизировать этот процесс с помощью электронных таблиц. При выполнении практического задания по этой теме в комплексе повторяются возможности программы Excel: использование встроенных функций, копирование формул, применение условного форматирования.
Задание: функция, зависящая от 4 переменных, задана своей таблицей истинности. Нужно построить полином Жегалкина в Excel
| х1 | х2 | х3 | х4 | f |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Решение

Скопировать таблицу в Excel.
Выделить всю таблицу 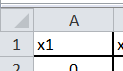 , сделать столбцы ỳже.
, сделать столбцы ỳже.
После таблицы пропускаем пустой столбец, далее будем строить треугольник:
Во второй строке выделяем 16 клеток, печатаем =ТРАНСП(
выделяем мышью столбец со значениями функции, закрываем скобку;
нажимаем CTRL + SHIFT + ENTER:
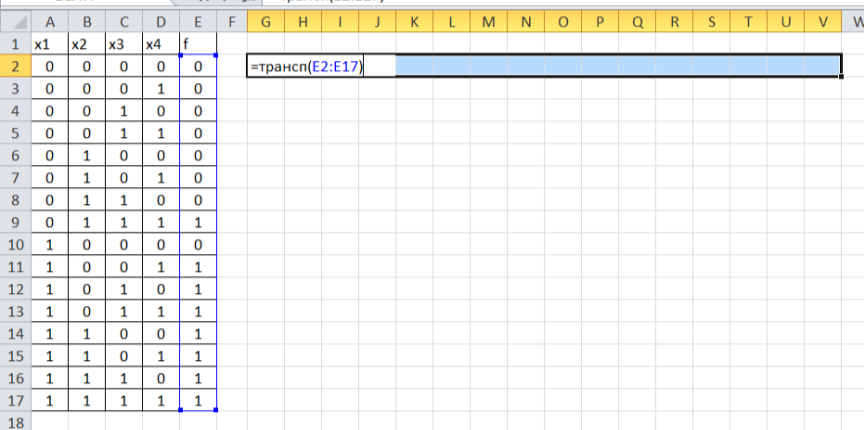
будем складывать по два числа и находить остаток от деления этой суммы на 2:
в клетке G3 пишем = ОСТАТ(
мышью выделяем G2
ставим плюс
мышью выделяем Н2
ставим точку с запятой
печатаем цифру 2
закрываем скобку
Enter
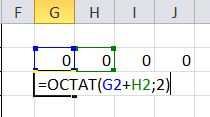
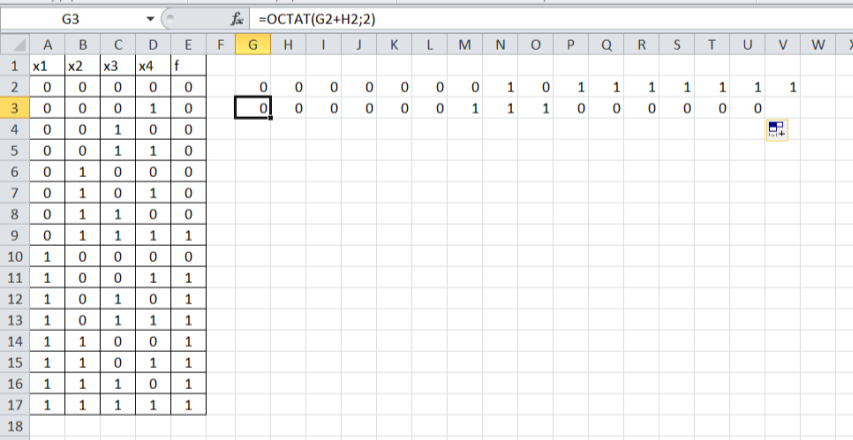
Копируем формулу вправо на 15 клеток:
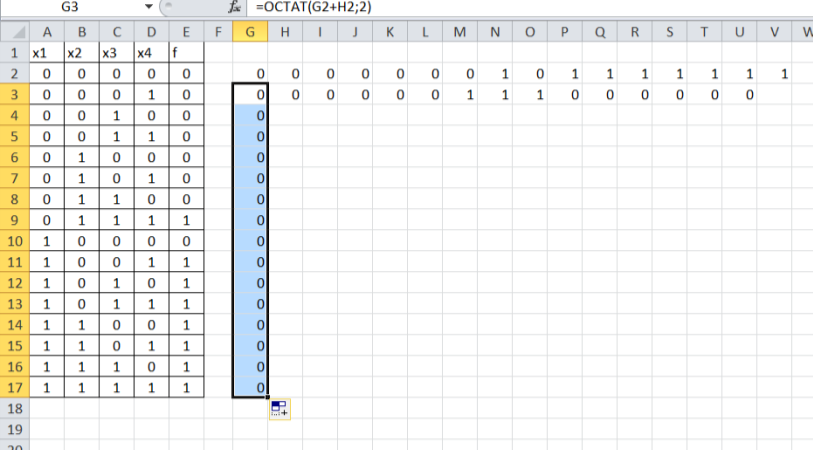
Копируем эту формулу вниз:
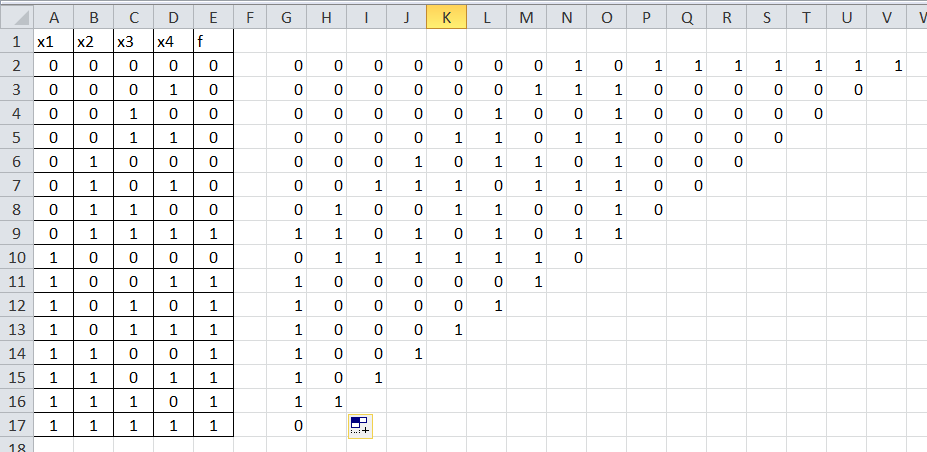
Каждую формулу из столбца G копируем вправо, заполняя на 1 клетку меньше, чем в предыдущей строке:
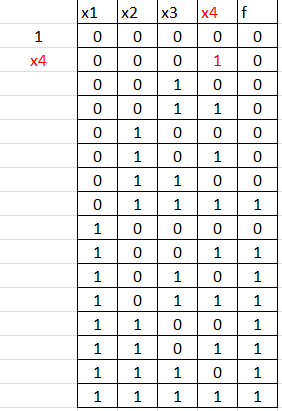
Теперь нужно записать те слагаемые, напротив чьих строчек стоят 1:
Перед столбцом А добавляем ещё один.
В строке, где 0000 в ячейке А2 пишем 1
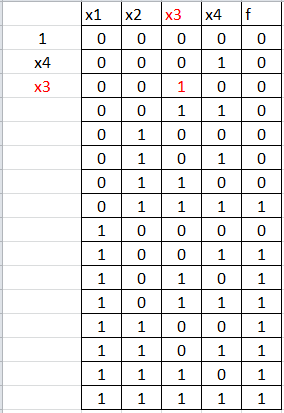
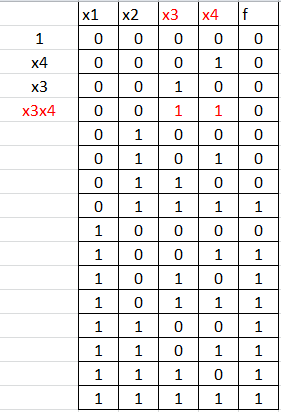
Далее записываем те х, напротив которых стоят 1:
 и т.д.
и т.д.
В ответ (в полином Жегалкина) нужно выписать слагаемые напротив единичек. Или так, НЕ выписывать слагаемые напротив нулей из левого столбца получившегося треугольника: нужно, чтобы напротив нулей из левого столбца треугольника слагаемые из столбца А закрасились белым цветом.
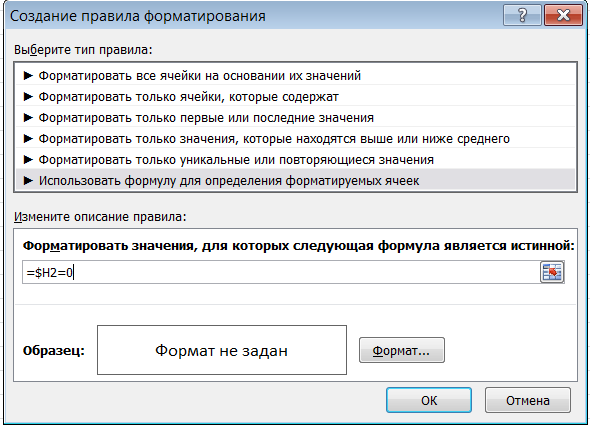
Выделяем столбец со слагаемыми (А), нажимаем условное форматирование, создать правило – использовать формулу для определения форматируемых ячеек:

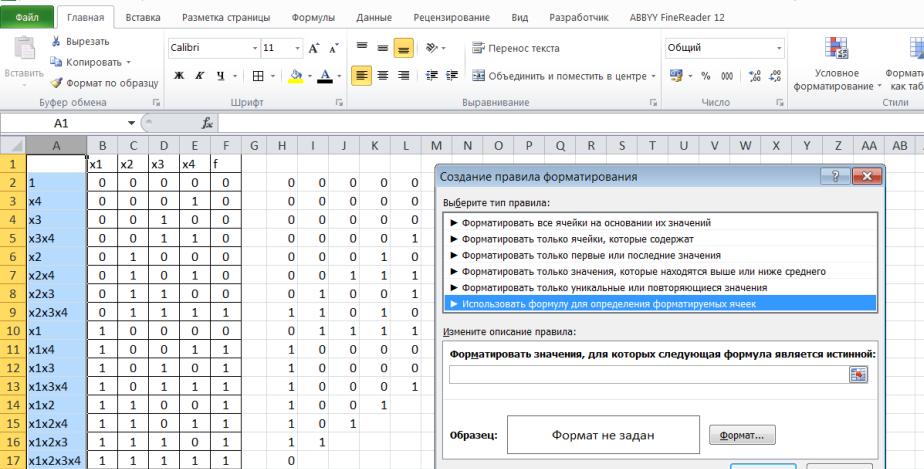
Нужно записать, что если в столбце Н число 0, но нужно применить белый цвет текста. Поэтому пишем формулу: =$H2=0 Доллар означает, что формула будет работать для этого зафиксированного столбца.
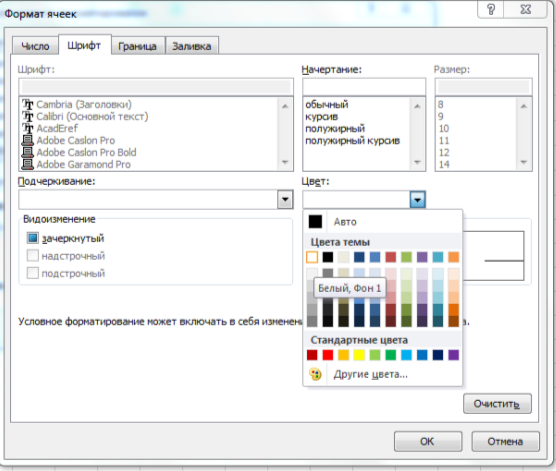
Нажимаем Формат…, и на вкладке Шрифт выбираем белый цвет текста:
Ок, Ок.
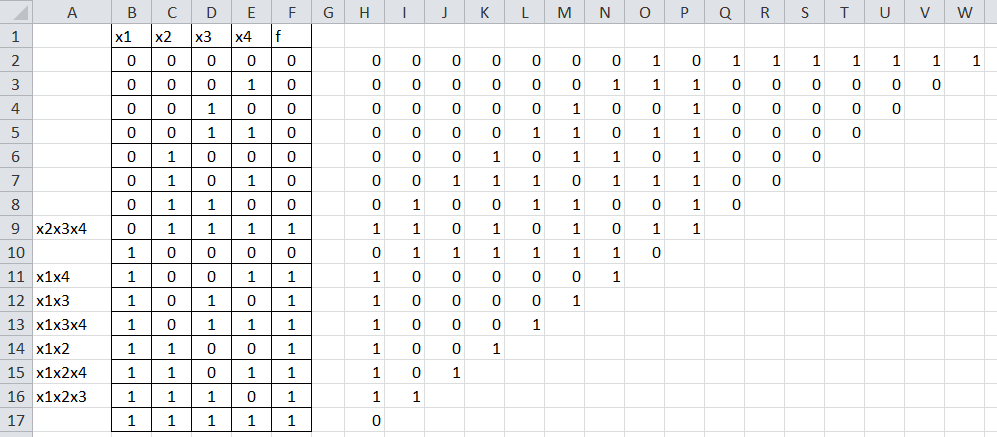
Слагаемые, оставшиеся в столбце А и будут входить в полином Жегалкина.
Проверяем универсальность таблицы, то есть, то, что при изменении значений функции перерасчет должен происходить автоматически:
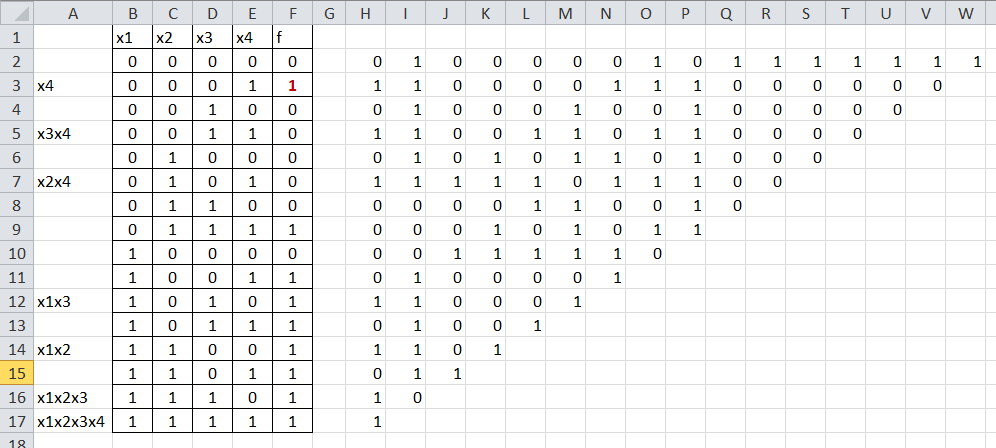
Такой алгоритм решения был придуман вместе со студентами; возможно, есть более универсальный способ, однако, здесь ценно было именно то, что обучающиеся смогли применить свои знания и умения и упростить решение задачи с помощью возможностей электронных таблиц.
Использование офисных программ на уроках математикидля преподавателей
Текстовый редактор – это замечательный инструмент для создания дидактического материала, который позволяет оформлять индивидуальные карточки для работы на занятии.
Электронные таблицы автоматизируют расчеты для составления многовариантных однотипных заданий. Например, проверочная работа по линейным, квадратным и дробно рациональным уравнениям представлена в 12 вариантах, поскольку Excel позволяет вычислить корни уравнения для любых коэффициентов, копирование формул оптимизирует процесс создания дидактического материала; при желании можно использовать функцию подбора данных, чтобы получились «красивые» ответы.
Удобно выставлять оценки, если используется балльная (рейтинговая) система, например:
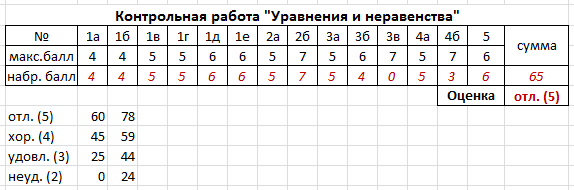
Оценка выставляется автоматически с помощью формулы.
При изучении элементов математической статистики студентам даётся следующее домашнее задание: записать рост любых 8 человек в группе. Найти моду, медиану, размах, среднее арифметическое, абсолютные и относительные частоты.
Для проверки вручную такого домашнего задания уйдет много времени, т.к. у студентов будут разные исходные данные и соответственно разные результаты.
Здесь удобно использовать заготовку в программе Excel:
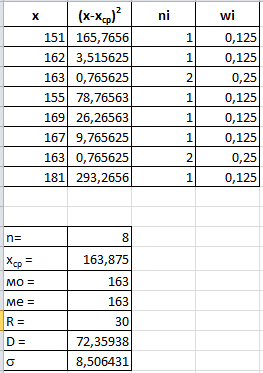
Достаточно внести другие данные в первый столбец, и программа автоматически пересчитает статистические характеристики:
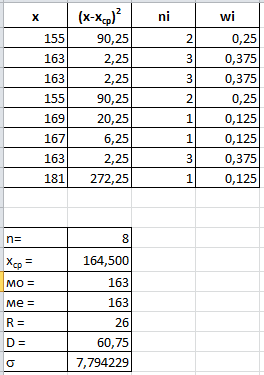
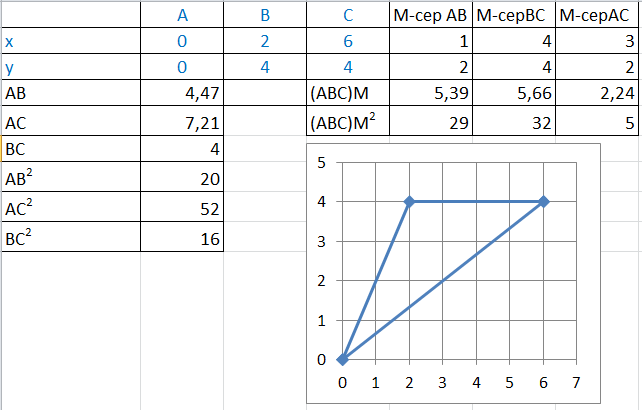
При повторении темы «Прямоугольная декартова система координат на плоскости» студентам в качестве домашнего задания предлагается следующее: в прямоугольной системе координат построить произвольный треугольник и одну его медиану. Найти:
Координаты его вершин;
Длины его сторон;
Длину медианы.
Для проверки удобно использовать заготовку в программе Excel: достаточно внести исходные данные, которые выделены синим цветом, и расчеты будут выполнены автоматически:
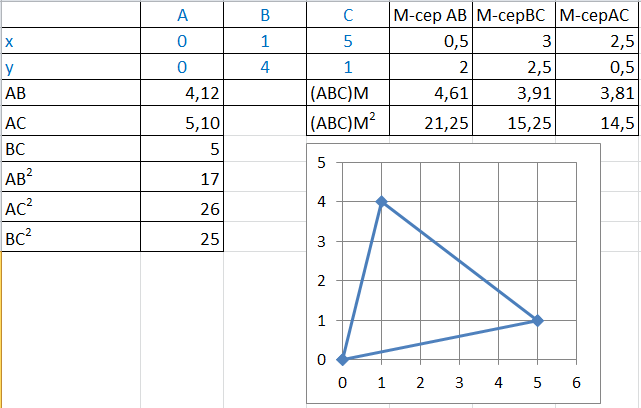
Очень пригодилась автоматизация выставления оценок при проверке работ во время дистанционного обучения. Студент получал не только оценку, но и видел по таблице с баллами, в каких заданиях он допустил ошибки.
ЗаключениеВ данной методической разработке представлен опыт проведения занятий по математике с использованием компьютерных технологий.
Хочется отметить, что все обучающиеся были включены в работу. Поскольку студентам были даны четкие пошаговые инструкции, все добились успеха в той или иной степени, урок не прошел впустую. Многие отметили, что на компьютере выполнять работу интереснее, чем в тетради.
Конечно, есть и сложности в организации подобного учебного процесса: в кабинете компьютеров меньше, чем обучающихся, поэтому некоторые выполняли работу в парах. Однако во время дистанционного обучения студенты занимались самостоятельно, в удобном для себя режиме и довольно качественно.
В дальнейшем планирую проводить подобные занятия с использованием офисных программ, а также разрабатывать новые задания для повышения мотивации обучающихся к изучению математики.
Повышение мотивации и качества обучения через новые формы, методы и приёмы (электронный ресурс: https://infourok.ru/povyshenie-motivacii-i-kachestva-obucheniya-cherez-novye-formy-metody-i-priyomy-5080529.html)
Морозкина А. А. Применение компьютерных технологий на уроках математики (электронный ресурс: https://infourok.ru/primenenie-kompyuternih-tehnologiy-na-urokah-matematiki-332622.html)
Гайнатуллина М.В. Использование электронных таблиц Microsoft Excel на уроках математики (электронный ресурс: https://urok.1sept.ru/articles/613869)

 Получите свидетельство
Получите свидетельство Вход
Вход




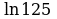
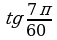
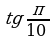
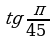
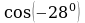
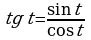 .
.









 Использование офисных программ на уроках математики (932.19 KB)
Использование офисных программ на уроках математики (932.19 KB)
 0
0 113
113 0
0 Нравится
0
Нравится
0



